High-dimensional robust regression under heavy-tailed data: Asymptotics and Universality

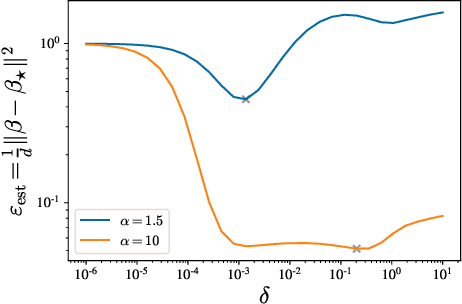
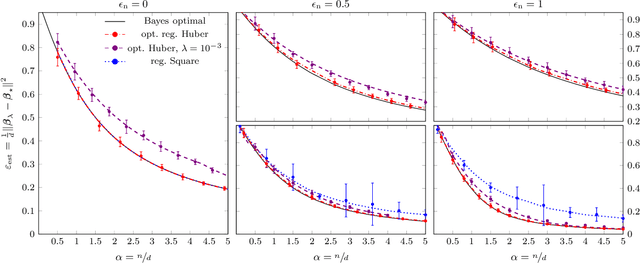
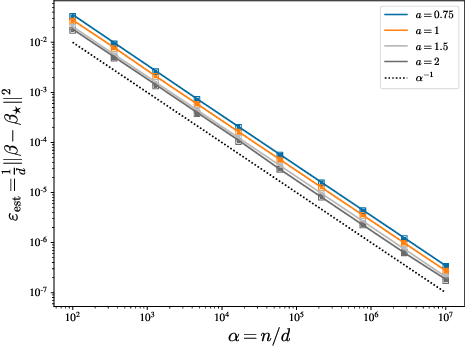
We investigate the high-dimensional properties of robust regression estimators in the presence of heavy-tailed contamination of both the covariates and response functions. In particular, we provide a sharp asymptotic characterisation of M-estimators trained on a family of elliptical covariate and noise data distributions including cases where second and higher moments do not exist. We show that, despite being consistent, the Huber loss with optimally tuned location parameter $\delta$ is suboptimal in the high-dimensional regime in the presence of heavy-tailed noise, highlighting the necessity of further regularisation to achieve optimal performance. This result also uncovers the existence of a curious transition in $\delta$ as a function of the sample complexity and contamination. Moreover, we derive the decay rates for the excess risk of ridge regression. We show that, while it is both optimal and universal for noise distributions with finite second moment, its decay rate can be considerably faster when the covariates' second moment does not exist. Finally, we show that our formulas readily generalise to a richer family of models and data distributions, such as generalised linear estimation with arbitrary convex regularisation trained on mixture models.

Unveiling the Hessian's Connection to the Decision Boundary

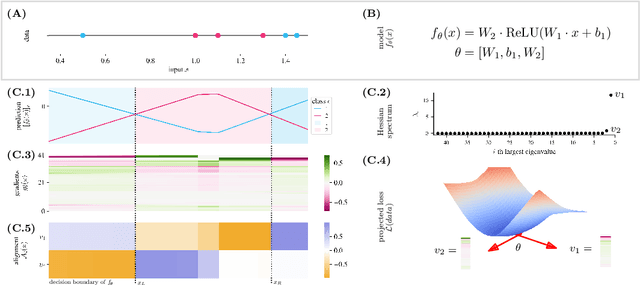
Understanding the properties of well-generalizing minima is at the heart of deep learning research. On the one hand, the generalization of neural networks has been connected to the decision boundary complexity, which is hard to study in the high-dimensional input space. Conversely, the flatness of a minimum has become a controversial proxy for generalization. In this work, we provide the missing link between the two approaches and show that the Hessian top eigenvectors characterize the decision boundary learned by the neural network. Notably, the number of outliers in the Hessian spectrum is proportional to the complexity of the decision boundary. Based on this finding, we provide a new and straightforward approach to studying the complexity of a high-dimensional decision boundary; show that this connection naturally inspires a new generalization measure; and finally, we develop a novel margin estimation technique which, in combination with the generalization measure, precisely identifies minima with simple wide-margin boundaries. Overall, this analysis establishes the connection between the Hessian and the decision boundary and provides a new method to identify minima with simple wide-margin decision boundaries.

Classification of Superstatistical Features in High Dimensions

We characterise the learning of a mixture of two clouds of data points with generic centroids via empirical risk minimisation in the high dimensional regime, under the assumptions of generic convex loss and convex regularisation. Each cloud of data points is obtained by sampling from a possibly uncountable superposition of Gaussian distributions, whose variance has a generic probability density $\varrho$. Our analysis covers therefore a large family of data distributions, including the case of power-law-tailed distributions with no covariance. We study the generalisation performance of the obtained estimator, we analyse the role of regularisation, and the dependence of the separability transition on the distribution scale parameters.