Dimension-free deterministic equivalents for random feature regression

In this work we investigate the generalization performance of random feature ridge regression (RFRR). Our main contribution is a general deterministic equivalent for the test error of RFRR. Specifically, under a certain concentration property, we show that the test error is well approximated by a closed-form expression that only depends on the feature map eigenvalues. Notably, our approximation guarantee is non-asymptotic, multiplicative, and independent of the feature map dimension -- allowing for infinite-dimensional features. We expect this deterministic equivalent to hold broadly beyond our theoretical analysis, and we empirically validate its predictions on various real and synthetic datasets. As an application, we derive sharp excess error rates under standard power-law assumptions of the spectrum and target decay. In particular, we provide a tight result for the smallest number of features achieving optimal minimax error rate.

Fundamental limits of weak learnability in high-dimensional multi-index models

Multi-index models -- functions which only depend on the covariates through a non-linear transformation of their projection on a subspace -- are a useful benchmark for investigating feature learning with neural networks. This paper examines the theoretical boundaries of learnability in this hypothesis class, focusing particularly on the minimum sample complexity required for weakly recovering their low-dimensional structure with first-order iterative algorithms, in the high-dimensional regime where the number of samples is $n=\alpha d$ is proportional to the covariate dimension $d$. Our findings unfold in three parts: (i) first, we identify under which conditions a \textit{trivial subspace} can be learned with a single step of a first-order algorithm for any $\alpha\!>\!0$; (ii) second, in the case where the trivial subspace is empty, we provide necessary and sufficient conditions for the existence of an {\it easy subspace} consisting of directions that can be learned only above a certain sample complexity $\alpha\!>\!\alpha_c$. The critical threshold $\alpha_{c}$ marks the presence of a computational phase transition, in the sense that no efficient iterative algorithm can succeed for $\alpha\!<\!\alpha_c$. In a limited but interesting set of really hard directions -- akin to the parity problem -- $\alpha_c$ is found to diverge. Finally, (iii) we demonstrate that interactions between different directions can result in an intricate hierarchical learning phenomenon, where some directions can be learned sequentially when coupled to easier ones. Our analytical approach is built on the optimality of approximate message-passing algorithms among first-order iterative methods, delineating the fundamental learnability limit across a broad spectrum of algorithms, including neural networks trained with gradient descent.

High-dimensional robust regression under heavy-tailed data: Asymptotics and Universality

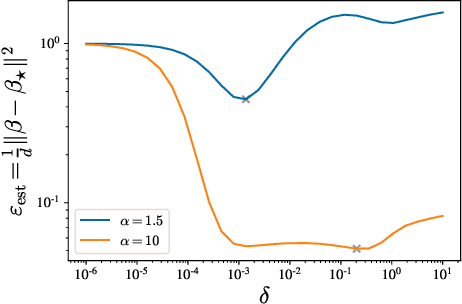
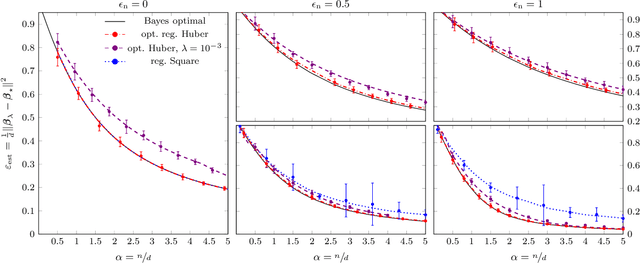
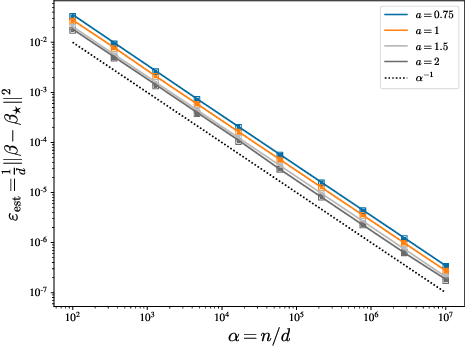
We investigate the high-dimensional properties of robust regression estimators in the presence of heavy-tailed contamination of both the covariates and response functions. In particular, we provide a sharp asymptotic characterisation of M-estimators trained on a family of elliptical covariate and noise data distributions including cases where second and higher moments do not exist. We show that, despite being consistent, the Huber loss with optimally tuned location parameter $\delta$ is suboptimal in the high-dimensional regime in the presence of heavy-tailed noise, highlighting the necessity of further regularisation to achieve optimal performance. This result also uncovers the existence of a curious transition in $\delta$ as a function of the sample complexity and contamination. Moreover, we derive the decay rates for the excess risk of ridge regression. We show that, while it is both optimal and universal for noise distributions with finite second moment, its decay rate can be considerably faster when the covariates' second moment does not exist. Finally, we show that our formulas readily generalise to a richer family of models and data distributions, such as generalised linear estimation with arbitrary convex regularisation trained on mixture models.