Emanuele Troiani
The Nuclear Route: Sharp Asymptotics of ERM in Overparameterized Quadratic Networks
May 23, 2025Abstract:We study the high-dimensional asymptotics of empirical risk minimization (ERM) in over-parametrized two-layer neural networks with quadratic activations trained on synthetic data. We derive sharp asymptotics for both training and test errors by mapping the $\ell_2$-regularized learning problem to a convex matrix sensing task with nuclear norm penalization. This reveals that capacity control in such networks emerges from a low-rank structure in the learned feature maps. Our results characterize the global minima of the loss and yield precise generalization thresholds, showing how the width of the target function governs learnability. This analysis bridges and extends ideas from spin-glass methods, matrix factorization, and convex optimization and emphasizes the deep link between low-rank matrix sensing and learning in quadratic neural networks.
Fundamental limits of learning in sequence multi-index models and deep attention networks: High-dimensional asymptotics and sharp thresholds
Feb 02, 2025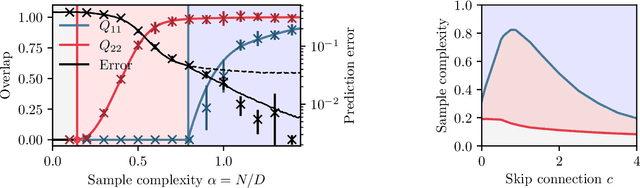
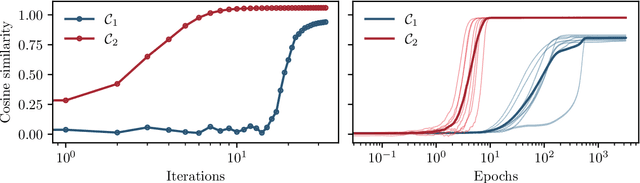
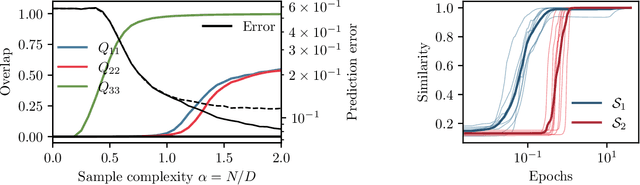
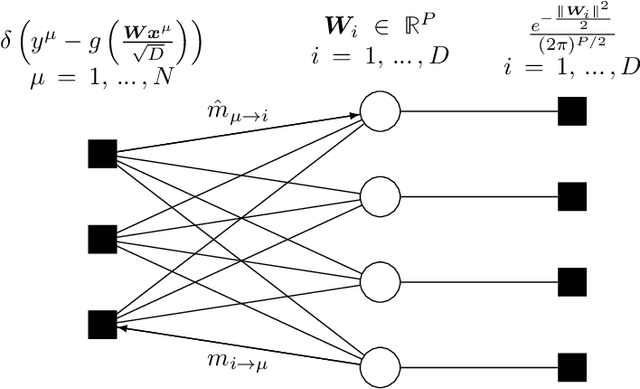
Abstract:In this manuscript, we study the learning of deep attention neural networks, defined as the composition of multiple self-attention layers, with tied and low-rank weights. We first establish a mapping of such models to sequence multi-index models, a generalization of the widely studied multi-index model to sequential covariates, for which we establish a number of general results. In the context of Bayesian-optimal learning, in the limit of large dimension $D$ and commensurably large number of samples $N$, we derive a sharp asymptotic characterization of the optimal performance as well as the performance of the best-known polynomial-time algorithm for this setting --namely approximate message-passing--, and characterize sharp thresholds on the minimal sample complexity required for better-than-random prediction performance. Our analysis uncovers, in particular, how the different layers are learned sequentially. Finally, we discuss how this sequential learning can also be observed in a realistic setup.
Bilinear Sequence Regression: A Model for Learning from Long Sequences of High-dimensional Tokens
Oct 24, 2024Abstract:Current progress in artificial intelligence is centered around so-called large language models that consist of neural networks processing long sequences of high-dimensional vectors called tokens. Statistical physics provides powerful tools to study the functioning of learning with neural networks and has played a recognized role in the development of modern machine learning. The statistical physics approach relies on simplified and analytically tractable models of data. However, simple tractable models for long sequences of high-dimensional tokens are largely underexplored. Inspired by the crucial role models such as the single-layer teacher-student perceptron (aka generalized linear regression) played in the theory of fully connected neural networks, in this paper, we introduce and study the bilinear sequence regression (BSR) as one of the most basic models for sequences of tokens. We note that modern architectures naturally subsume the BSR model due to the skip connections. Building on recent methodological progress, we compute the Bayes-optimal generalization error for the model in the limit of long sequences of high-dimensional tokens, and provide a message-passing algorithm that matches this performance. We quantify the improvement that optimal learning brings with respect to vectorizing the sequence of tokens and learning via simple linear regression. We also unveil surprising properties of the gradient descent algorithms in the BSR model.
Bayes-optimal learning of an extensive-width neural network from quadratically many samples
Aug 07, 2024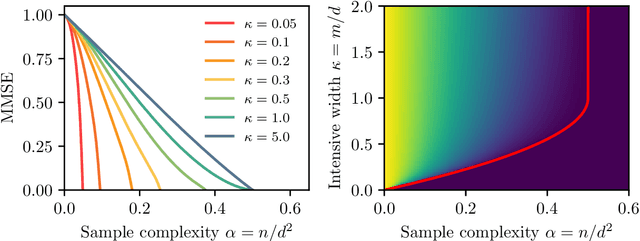
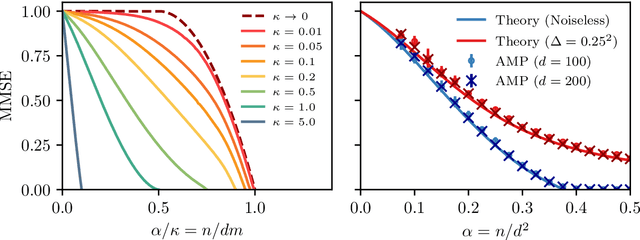
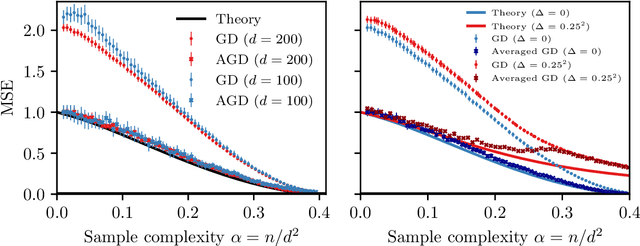
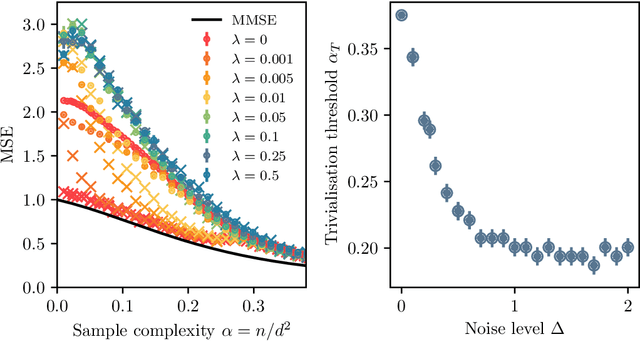
Abstract:We consider the problem of learning a target function corresponding to a single hidden layer neural network, with a quadratic activation function after the first layer, and random weights. We consider the asymptotic limit where the input dimension and the network width are proportionally large. Recent work [Cui & al '23] established that linear regression provides Bayes-optimal test error to learn such a function when the number of available samples is only linear in the dimension. That work stressed the open challenge of theoretically analyzing the optimal test error in the more interesting regime where the number of samples is quadratic in the dimension. In this paper, we solve this challenge for quadratic activations and derive a closed-form expression for the Bayes-optimal test error. We also provide an algorithm, that we call GAMP-RIE, which combines approximate message passing with rotationally invariant matrix denoising, and that asymptotically achieves the optimal performance. Technically, our result is enabled by establishing a link with recent works on optimal denoising of extensive-rank matrices and on the ellipsoid fitting problem. We further show empirically that, in the absence of noise, randomly-initialized gradient descent seems to sample the space of weights, leading to zero training loss, and averaging over initialization leads to a test error equal to the Bayes-optimal one.
Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants
Aug 07, 2024
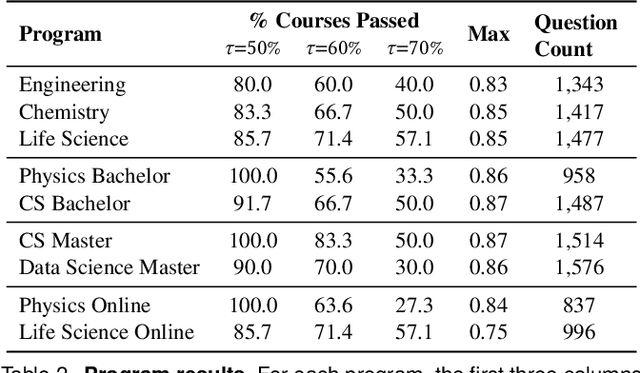

Abstract:AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.
Fundamental limits of weak learnability in high-dimensional multi-index models
May 24, 2024Abstract:Multi-index models -- functions which only depend on the covariates through a non-linear transformation of their projection on a subspace -- are a useful benchmark for investigating feature learning with neural networks. This paper examines the theoretical boundaries of learnability in this hypothesis class, focusing particularly on the minimum sample complexity required for weakly recovering their low-dimensional structure with first-order iterative algorithms, in the high-dimensional regime where the number of samples is $n=\alpha d$ is proportional to the covariate dimension $d$. Our findings unfold in three parts: (i) first, we identify under which conditions a \textit{trivial subspace} can be learned with a single step of a first-order algorithm for any $\alpha\!>\!0$; (ii) second, in the case where the trivial subspace is empty, we provide necessary and sufficient conditions for the existence of an {\it easy subspace} consisting of directions that can be learned only above a certain sample complexity $\alpha\!>\!\alpha_c$. The critical threshold $\alpha_{c}$ marks the presence of a computational phase transition, in the sense that no efficient iterative algorithm can succeed for $\alpha\!<\!\alpha_c$. In a limited but interesting set of really hard directions -- akin to the parity problem -- $\alpha_c$ is found to diverge. Finally, (iii) we demonstrate that interactions between different directions can result in an intricate hierarchical learning phenomenon, where some directions can be learned sequentially when coupled to easier ones. Our analytical approach is built on the optimality of approximate message-passing algorithms among first-order iterative methods, delineating the fundamental learnability limit across a broad spectrum of algorithms, including neural networks trained with gradient descent.
The Benefits of Reusing Batches for Gradient Descent in Two-Layer Networks: Breaking the Curse of Information and Leap Exponents
Feb 05, 2024

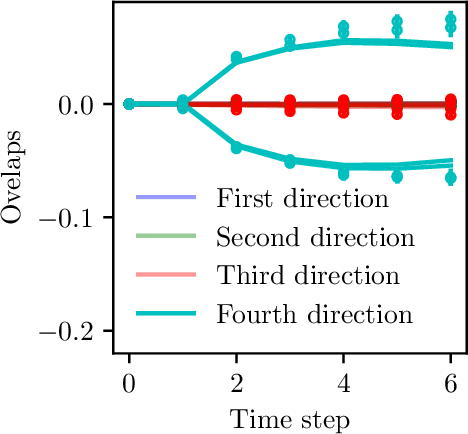
Abstract:We investigate the training dynamics of two-layer neural networks when learning multi-index target functions. We focus on multi-pass gradient descent (GD) that reuses the batches multiple times and show that it significantly changes the conclusion about which functions are learnable compared to single-pass gradient descent. In particular, multi-pass GD with finite stepsize is found to overcome the limitations of gradient flow and single-pass GD given by the information exponent (Ben Arous et al., 2021) and leap exponent (Abbe et al., 2023) of the target function. We show that upon re-using batches, the network achieves in just two time steps an overlap with the target subspace even for functions not satisfying the staircase property (Abbe et al., 2021). We characterize the (broad) class of functions efficiently learned in finite time. The proof of our results is based on the analysis of the Dynamical Mean-Field Theory (DMFT). We further provide a closed-form description of the dynamical process of the low-dimensional projections of the weights, and numerical experiments illustrating the theory.
Sparse Representations, Inference and Learning
Jun 28, 2023Abstract:In recent years statistical physics has proven to be a valuable tool to probe into large dimensional inference problems such as the ones occurring in machine learning. Statistical physics provides analytical tools to study fundamental limitations in their solutions and proposes algorithms to solve individual instances. In these notes, based on the lectures by Marc M\'ezard in 2022 at the summer school in Les Houches, we will present a general framework that can be used in a large variety of problems with weak long-range interactions, including the compressed sensing problem, or the problem of learning in a perceptron. We shall see how these problems can be studied at the replica symmetric level, using developments of the cavity methods, both as a theoretical tool and as an algorithm.
Gibbs Sampling the Posterior of Neural Networks
Jun 05, 2023Abstract:In this paper, we study sampling from a posterior derived from a neural network. We propose a new probabilistic model consisting of adding noise at every pre- and post-activation in the network, arguing that the resulting posterior can be sampled using an efficient Gibbs sampler. The Gibbs sampler attains similar performances as the state-of-the-art Monte Carlo Markov chain methods, such as the Hamiltonian Monte Carlo or the Metropolis adjusted Langevin algorithm, both on real and synthetic data. By framing our analysis in the teacher-student setting, we introduce a thermalization criterion that allows us to detect when an algorithm, when run on data with synthetic labels, fails to sample from the posterior. The criterion is based on the fact that in the teacher-student setting we can initialize an algorithm directly at equilibrium.
Asymptotic Characterisation of Robust Empirical Risk Minimisation Performance in the Presence of Outliers
May 30, 2023



Abstract:We study robust linear regression in high-dimension, when both the dimension $d$ and the number of data points $n$ diverge with a fixed ratio $\alpha=n/d$, and study a data model that includes outliers. We provide exact asymptotics for the performances of the empirical risk minimisation (ERM) using $\ell_2$-regularised $\ell_2$, $\ell_1$, and Huber loss, which are the standard approach to such problems. We focus on two metrics for the performance: the generalisation error to similar datasets with outliers, and the estimation error of the original, unpolluted function. Our results are compared with the information theoretic Bayes-optimal estimation bound. For the generalization error, we find that optimally-regularised ERM is asymptotically consistent in the large sample complexity limit if one perform a simple calibration, and compute the rates of convergence. For the estimation error however, we show that due to a norm calibration mismatch, the consistency of the estimator requires an oracle estimate of the optimal norm, or the presence of a cross-validation set not corrupted by the outliers. We examine in detail how performance depends on the loss function and on the degree of outlier corruption in the training set and identify a region of parameters where the optimal performance of the Huber loss is identical to that of the $\ell_2$ loss, offering insights into the use cases of different loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge