The Spoils of Algorithmic Collusion: Profit Allocation Among Asymmetric Firms

We study the propensity of independent algorithms to collude in repeated Cournot duopoly games. Specifically, we investigate the predictive power of different oligopoly and bargaining solutions regarding the effect of asymmetry between firms. We find that both consumers and firms can benefit from asymmetry. Algorithms produce more competitive outcomes when firms are symmetric, but less when they are very asymmetric. Although the static Nash equilibrium underestimates the effect on total quantity and overestimates the effect on profits, it delivers surprisingly accurate predictions in terms of total welfare. The best description of our results is provided by the equal relative gains solution. In particular, we find algorithms to agree on profits that are on or close to the Pareto frontier for all degrees of asymmetry. Our results suggest that the common belief that symmetric industries are more prone to collusion may no longer hold when algorithms increasingly drive managerial decisions.

Bayes-optimal learning of an extensive-width neural network from quadratically many samples

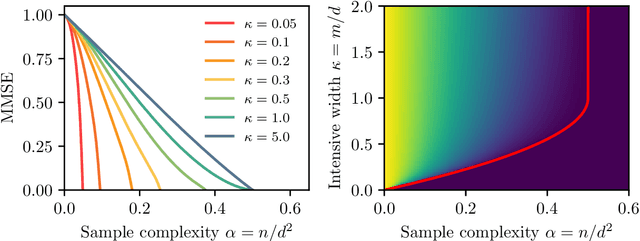
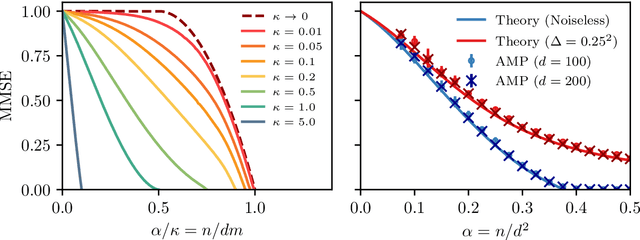
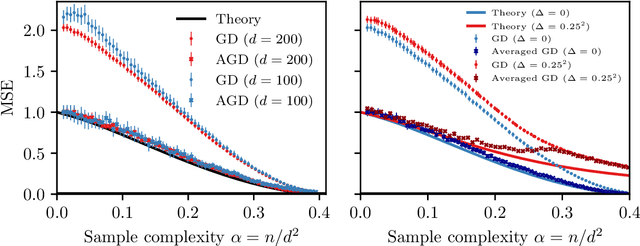
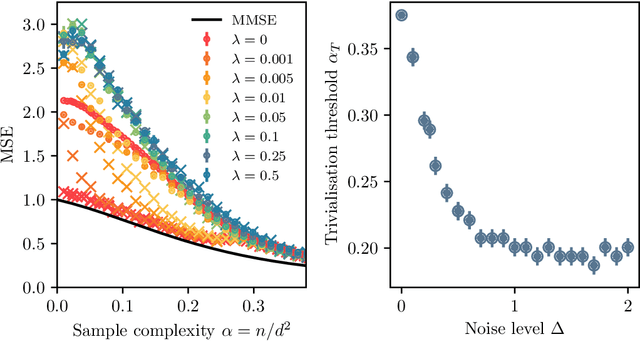
We consider the problem of learning a target function corresponding to a single hidden layer neural network, with a quadratic activation function after the first layer, and random weights. We consider the asymptotic limit where the input dimension and the network width are proportionally large. Recent work [Cui & al '23] established that linear regression provides Bayes-optimal test error to learn such a function when the number of available samples is only linear in the dimension. That work stressed the open challenge of theoretically analyzing the optimal test error in the more interesting regime where the number of samples is quadratic in the dimension. In this paper, we solve this challenge for quadratic activations and derive a closed-form expression for the Bayes-optimal test error. We also provide an algorithm, that we call GAMP-RIE, which combines approximate message passing with rotationally invariant matrix denoising, and that asymptotically achieves the optimal performance. Technically, our result is enabled by establishing a link with recent works on optimal denoising of extensive-rank matrices and on the ellipsoid fitting problem. We further show empirically that, in the absence of noise, randomly-initialized gradient descent seems to sample the space of weights, leading to zero training loss, and averaging over initialization leads to a test error equal to the Bayes-optimal one.

Multi-Modal Dataset Creation for Federated~Learning with DICOM Structured Reports

Purpose: Federated training is often hindered by heterogeneous datasets due to divergent data storage options, inconsistent naming schemes, varied annotation procedures, and disparities in label quality. This is particularly evident in the emerging multi-modal learning paradigms, where dataset harmonization including a uniform data representation and filtering options are of paramount importance. Methods: DICOM structured reports enable the standardized linkage of arbitrary information beyond the imaging domain and can be used within Python deep learning pipelines with highdicom. Building on this, we developed an open platform for data integration and interactive filtering capabilities that simplifies the process of assembling multi-modal datasets. Results: In this study, we extend our prior work by showing its applicability to more and divergent data types, as well as streamlining datasets for federated training within an established consortium of eight university hospitals in Germany. We prove its concurrent filtering ability by creating harmonized multi-modal datasets across all locations for predicting the outcome after minimally invasive heart valve replacement. The data includes DICOM data (i.e. computed tomography images, electrocardiography scans) as well as annotations (i.e. calcification segmentations, pointsets and pacemaker dependency), and metadata (i.e. prosthesis and diagnoses). Conclusion: Structured reports bridge the traditional gap between imaging systems and information systems. Utilizing the inherent DICOM reference system arbitrary data types can be queried concurrently to create meaningful cohorts for clinical studies. The graphical interface as well as example structured report templates will be made publicly available.

Federated Foundation Model for Cardiac CT Imaging

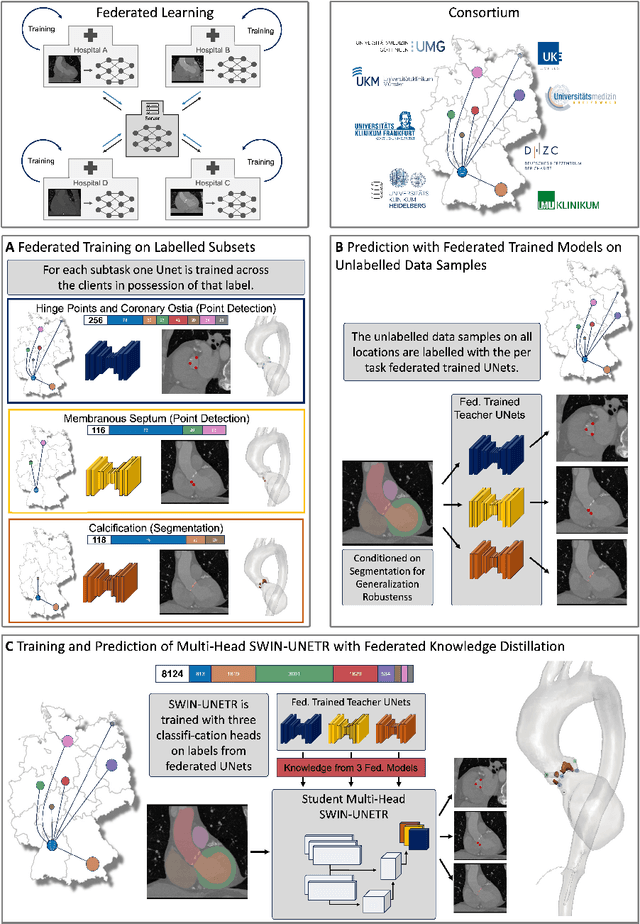
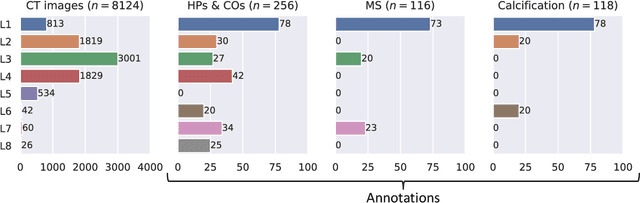
Federated learning (FL) is a renowned technique for utilizing decentralized data while preserving privacy. However, real-world applications often involve inherent challenges such as partially labeled datasets, where not all clients possess expert annotations of all labels of interest, leaving large portions of unlabeled data unused. In this study, we conduct the largest federated cardiac CT imaging analysis to date, focusing on partially labeled datasets ($n=8,124$) of Transcatheter Aortic Valve Implantation (TAVI) patients over eight hospital clients. Transformer architectures, which are the major building blocks of current foundation models, have shown superior performance when trained on larger cohorts than traditional CNNs. However, when trained on small task-specific labeled sample sizes, it is currently not feasible to exploit their underlying attention mechanism for improved performance. Therefore, we developed a two-stage semi-supervised learning strategy that distills knowledge from several task-specific CNNs (landmark detection and segmentation of calcification) into a single transformer model by utilizing large amounts of unlabeled data typically residing unused in hospitals to mitigate these issues. This method not only improves the predictive accuracy and generalizability of transformer-based architectures but also facilitates the simultaneous learning of all partial labels within a single transformer model across the federation. Additionally, we show that our transformer-based model extracts more meaningful features for further downstream tasks than the UNet-based one by only training the last layer to also solve segmentation of coronary arteries. We make the code and weights of the final model openly available, which can serve as a foundation model for further research in cardiac CT imaging.

On the Impact of Overparameterization on the Training of a Shallow Neural Network in High Dimensions

We study the training dynamics of a shallow neural network with quadratic activation functions and quadratic cost in a teacher-student setup. In line with previous works on the same neural architecture, the optimization is performed following the gradient flow on the population risk, where the average over data points is replaced by the expectation over their distribution, assumed to be Gaussian.We first derive convergence properties for the gradient flow and quantify the overparameterization that is necessary to achieve a strong signal recovery. Then, assuming that the teachers and the students at initialization form independent orthonormal families, we derive a high-dimensional limit for the flow and show that the minimal overparameterization is sufficient for strong recovery. We verify by numerical experiments that these results hold for more general initializations.