Bilinear Sequence Regression: A Model for Learning from Long Sequences of High-dimensional Tokens

Current progress in artificial intelligence is centered around so-called large language models that consist of neural networks processing long sequences of high-dimensional vectors called tokens. Statistical physics provides powerful tools to study the functioning of learning with neural networks and has played a recognized role in the development of modern machine learning. The statistical physics approach relies on simplified and analytically tractable models of data. However, simple tractable models for long sequences of high-dimensional tokens are largely underexplored. Inspired by the crucial role models such as the single-layer teacher-student perceptron (aka generalized linear regression) played in the theory of fully connected neural networks, in this paper, we introduce and study the bilinear sequence regression (BSR) as one of the most basic models for sequences of tokens. We note that modern architectures naturally subsume the BSR model due to the skip connections. Building on recent methodological progress, we compute the Bayes-optimal generalization error for the model in the limit of long sequences of high-dimensional tokens, and provide a message-passing algorithm that matches this performance. We quantify the improvement that optimal learning brings with respect to vectorizing the sequence of tokens and learning via simple linear regression. We also unveil surprising properties of the gradient descent algorithms in the BSR model.

Bayes-optimal learning of an extensive-width neural network from quadratically many samples

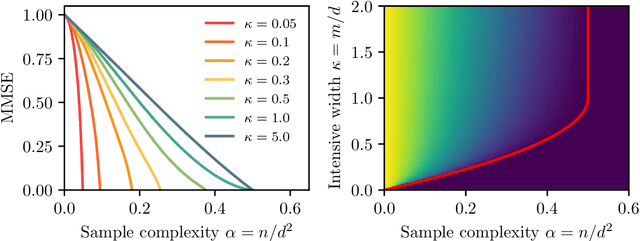
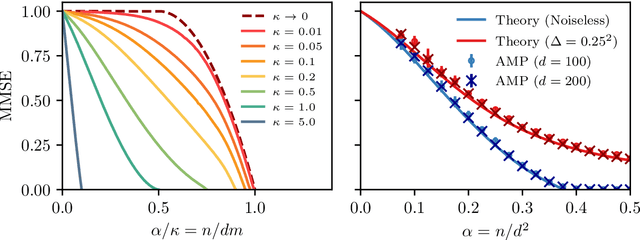
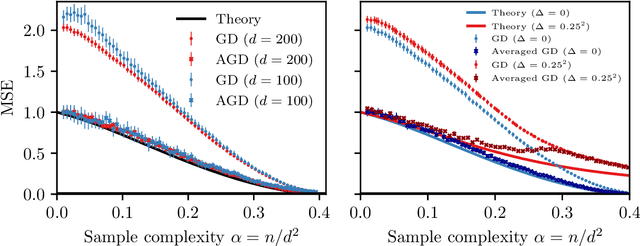
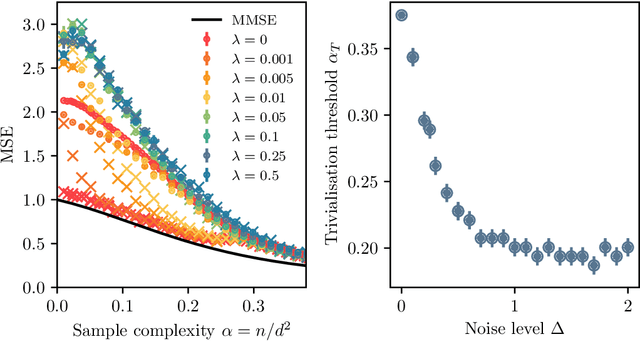
We consider the problem of learning a target function corresponding to a single hidden layer neural network, with a quadratic activation function after the first layer, and random weights. We consider the asymptotic limit where the input dimension and the network width are proportionally large. Recent work [Cui & al '23] established that linear regression provides Bayes-optimal test error to learn such a function when the number of available samples is only linear in the dimension. That work stressed the open challenge of theoretically analyzing the optimal test error in the more interesting regime where the number of samples is quadratic in the dimension. In this paper, we solve this challenge for quadratic activations and derive a closed-form expression for the Bayes-optimal test error. We also provide an algorithm, that we call GAMP-RIE, which combines approximate message passing with rotationally invariant matrix denoising, and that asymptotically achieves the optimal performance. Technically, our result is enabled by establishing a link with recent works on optimal denoising of extensive-rank matrices and on the ellipsoid fitting problem. We further show empirically that, in the absence of noise, randomly-initialized gradient descent seems to sample the space of weights, leading to zero training loss, and averaging over initialization leads to a test error equal to the Bayes-optimal one.

Fitting an ellipsoid to a quadratic number of random points

We consider the problem $(\mathrm{P})$ of fitting $n$ standard Gaussian random vectors in $\mathbb{R}^d$ to the boundary of a centered ellipsoid, as $n, d \to \infty$. This problem is conjectured to have a sharp feasibility transition: for any $\varepsilon > 0$, if $n \leq (1 - \varepsilon) d^2 / 4$ then $(\mathrm{P})$ has a solution with high probability, while $(\mathrm{P})$ has no solutions with high probability if $n \geq (1 + \varepsilon) d^2 /4$. So far, only a trivial bound $n \geq d^2 / 2$ is known on the negative side, while the best results on the positive side assume $n \leq d^2 / \mathrm{polylog}(d)$. In this work, we improve over previous approaches using a key result of Bartl & Mendelson on the concentration of Gram matrices of random vectors under mild assumptions on their tail behavior. This allows us to give a simple proof that $(\mathrm{P})$ is feasible with high probability when $n \leq d^2 / C$, for a (possibly large) constant $C > 0$.

Injectivity of ReLU networks: perspectives from statistical physics

When can the input of a ReLU neural network be inferred from its output? In other words, when is the network injective? We consider a single layer, $x \mapsto \mathrm{ReLU}(Wx)$, with a random Gaussian $m \times n$ matrix $W$, in a high-dimensional setting where $n, m \to \infty$. Recent work connects this problem to spherical integral geometry giving rise to a conjectured sharp injectivity threshold for $\alpha = \frac{m}{n}$ by studying the expected Euler characteristic of a certain random set. We adopt a different perspective and show that injectivity is equivalent to a property of the ground state of the spherical perceptron, an important spin glass model in statistical physics. By leveraging the (non-rigorous) replica symmetry-breaking theory, we derive analytical equations for the threshold whose solution is at odds with that from the Euler characteristic. Furthermore, we use Gordon's min--max theorem to prove that a replica-symmetric upper bound refutes the Euler characteristic prediction. Along the way we aim to give a tutorial-style introduction to key ideas from statistical physics in an effort to make the exposition accessible to a broad audience. Our analysis establishes a connection between spin glasses and integral geometry but leaves open the problem of explaining the discrepancies.

On free energy barriers in Gaussian priors and failure of MCMC for high-dimensional unimodal distributions

We exhibit examples of high-dimensional unimodal posterior distributions arising in non-linear regression models with Gaussian process priors for which worst-case (`cold start') initialised MCMC methods typically take an exponential run-time to enter the regions where the bulk of the posterior measure concentrates. The counter-examples hold for general MCMC schemes based on gradient or random walk steps, and the theory is illustrated for Metropolis-Hastings adjusted methods such as pCN and MALA.

Phase retrieval in high dimensions: Statistical and computational phase transitions

We consider the phase retrieval problem of reconstructing a $n$-dimensional real or complex signal $\mathbf{X}^{\star}$ from $m$ (possibly noisy) observations $Y_\mu = | \sum_{i=1}^n \Phi_{\mu i} X^{\star}_i/\sqrt{n}|$, for a large class of correlated real and complex random sensing matrices $\mathbf{\Phi}$, in a high-dimensional setting where $m,n\to\infty$ while $\alpha = m/n=\Theta(1)$. First, we derive sharp asymptotics for the lowest possible estimation error achievable statistically and we unveil the existence of sharp phase transitions for the weak- and full-recovery thresholds as a function of the singular values of the matrix $\mathbf{\Phi}$. This is achieved by providing a rigorous proof of a result first obtained by the replica method from statistical mechanics. In particular, the information-theoretic transition to perfect recovery for full-rank matrices appears at $\alpha=1$ (real case) and $\alpha=2$ (complex case). Secondly, we analyze the performance of the best-known polynomial time algorithm for this problem -- approximate message-passing -- establishing the existence of a statistical-to-algorithmic gap depending, again, on the spectral properties of $\mathbf{\Phi}$. Our work provides an extensive classification of the statistical and algorithmic thresholds in high-dimensional phase retrieval for a broad class of random matrices.

Landscape Complexity for the Empirical Risk of Generalized Linear Models

We present a method to obtain the average and the typical value of the number of critical points of the empirical risk landscape for generalized linear estimation problems and variants. This represents a substantial extension of previous applications of the Kac-Rice method since it allows to analyze the critical points of high dimensional non-Gaussian random functions. We obtain a rigorous explicit variational formula for the annealed complexity, which is the logarithm of the average number of critical points at fixed value of the empirical risk. This result is simplified, and extended, using the non-rigorous Kac-Rice replicated method from theoretical physics. In this way we find an explicit variational formula for the quenched complexity, which is generally different from its annealed counterpart, and allows to obtain the number of critical points for typical instances up to exponential accuracy.

The spiked matrix model with generative priors

Using a low-dimensional parametrization of signals is a generic and powerful way to enhance performance in signal processing and statistical inference. A very popular and widely explored type of dimensionality reduction is sparsity; another type is generative modelling of signal distributions. Generative models based on neural networks, such as GANs or variational auto-encoders, are particularly performant and are gaining on applicability. In this paper we study spiked matrix models, where a low-rank matrix is observed through a noisy channel. This problem with sparse structure of the spikes has attracted broad attention in the past literature. Here, we replace the sparsity assumption by generative modelling, and investigate the consequences on statistical and algorithmic properties. We analyze the Bayes-optimal performance under specific generative models for the spike. In contrast with the sparsity assumption, we do not observe regions of parameters where statistical performance is superior to the best known algorithmic performance. We show that in the analyzed cases the approximate message passing algorithm is able to reach optimal performance. We also design enhanced spectral algorithms and analyze their performance and thresholds using random matrix theory, showing their superiority to the classical principal component analysis. We complement our theoretical results by illustrating the performance of the spectral algorithms when the spikes come from real datasets.

The committee machine: Computational to statistical gaps in learning a two-layers neural network

Heuristic tools from statistical physics have been used in the past to locate the phase transitions and compute the optimal learning and generalization errors in the teacher-student scenario in multi-layer neural networks. In this contribution, we provide a rigorous justification of these approaches for a two-layers neural network model called the committee machine. We also introduce a version of the approximate message passing (AMP) algorithm for the committee machine that allows to perform optimal learning in polynomial time for a large set of parameters. We find that there are regimes in which a low generalization error is information-theoretically achievable while the AMP algorithm fails to deliver it, strongly suggesting that no efficient algorithm exists for those cases, and unveiling a large computational gap.