Asymptotics of Non-Convex Generalized Linear Models in High-Dimensions: A proof of the replica formula

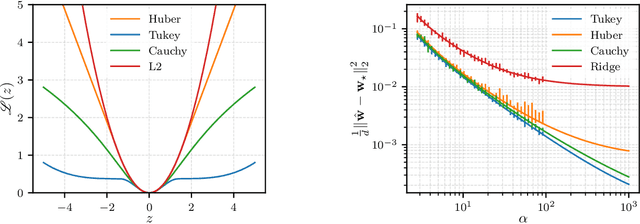
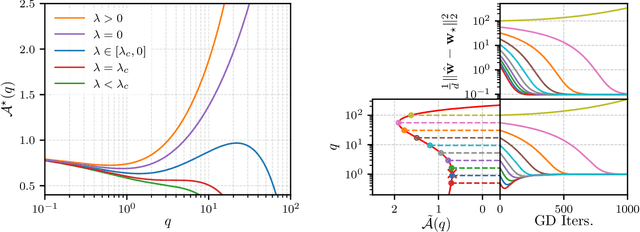
The analytic characterization of the high-dimensional behavior of optimization for Generalized Linear Models (GLMs) with Gaussian data has been a central focus in statistics and probability in recent years. While convex cases, such as the LASSO, ridge regression, and logistic regression, have been extensively studied using a variety of techniques, the non-convex case remains far less understood despite its significance. A non-rigorous statistical physics framework has provided remarkable predictions for the behavior of high-dimensional optimization problems, but rigorously establishing their validity for non-convex problems has remained a fundamental challenge. In this work, we address this challenge by developing a systematic framework that rigorously proves replica-symmetric formulas for non-convex GLMs and precisely determines the conditions under which these formulas are valid. Remarkably, the rigorous replica-symmetric predictions align exactly with the conjectures made by physicists, and the so-called replicon condition. The originality of our approach lies in connecting two powerful theoretical tools: the Gaussian Min-Max Theorem, which we use to provide precise lower bounds, and Approximate Message Passing (AMP), which is shown to achieve these bounds algorithmically. We demonstrate the utility of this framework through significant applications: (i) by proving the optimality of the Tukey loss over the more commonly used Huber loss under a $\varepsilon$ contaminated data model, (ii) establishing the optimality of negative regularization in high-dimensional non-convex regression and (iii) characterizing the performance limits of linearized AMP algorithms. By rigorously validating statistical physics predictions in non-convex settings, we aim to open new pathways for analyzing increasingly complex optimization landscapes beyond the convex regime.

On the Geometry of Regularization in Adversarial Training: High-Dimensional Asymptotics and Generalization Bounds

Regularization, whether explicit in terms of a penalty in the loss or implicit in the choice of algorithm, is a cornerstone of modern machine learning. Indeed, controlling the complexity of the model class is particularly important when data is scarce, noisy or contaminated, as it translates a statistical belief on the underlying structure of the data. This work investigates the question of how to choose the regularization norm $\lVert \cdot \rVert$ in the context of high-dimensional adversarial training for binary classification. To this end, we first derive an exact asymptotic description of the robust, regularized empirical risk minimizer for various types of adversarial attacks and regularization norms (including non-$\ell_p$ norms). We complement this analysis with a uniform convergence analysis, deriving bounds on the Rademacher Complexity for this class of problems. Leveraging our theoretical results, we quantitatively characterize the relationship between perturbation size and the optimal choice of $\lVert \cdot \rVert$, confirming the intuition that, in the data scarce regime, the type of regularization becomes increasingly important for adversarial training as perturbations grow in size.

A High Dimensional Model for Adversarial Training: Geometry and Trade-Offs

This work investigates adversarial training in the context of margin-based linear classifiers in the high-dimensional regime where the dimension $d$ and the number of data points $n$ diverge with a fixed ratio $\alpha = n / d$. We introduce a tractable mathematical model where the interplay between the data and adversarial attacker geometries can be studied, while capturing the core phenomenology observed in the adversarial robustness literature. Our main theoretical contribution is an exact asymptotic description of the sufficient statistics for the adversarial empirical risk minimiser, under generic convex and non-increasing losses. Our result allow us to precisely characterise which directions in the data are associated with a higher generalisation/robustness trade-off, as defined by a robustness and a usefulness metric. In particular, we unveil the existence of directions which can be defended without penalising accuracy. Finally, we show the advantage of defending non-robust features during training, identifying a uniform protection as an inherently effective defence mechanism.

Asymptotic Characterisation of Robust Empirical Risk Minimisation Performance in the Presence of Outliers

We study robust linear regression in high-dimension, when both the dimension $d$ and the number of data points $n$ diverge with a fixed ratio $\alpha=n/d$, and study a data model that includes outliers. We provide exact asymptotics for the performances of the empirical risk minimisation (ERM) using $\ell_2$-regularised $\ell_2$, $\ell_1$, and Huber loss, which are the standard approach to such problems. We focus on two metrics for the performance: the generalisation error to similar datasets with outliers, and the estimation error of the original, unpolluted function. Our results are compared with the information theoretic Bayes-optimal estimation bound. For the generalization error, we find that optimally-regularised ERM is asymptotically consistent in the large sample complexity limit if one perform a simple calibration, and compute the rates of convergence. For the estimation error however, we show that due to a norm calibration mismatch, the consistency of the estimator requires an oracle estimate of the optimal norm, or the presence of a cross-validation set not corrupted by the outliers. We examine in detail how performance depends on the loss function and on the degree of outlier corruption in the training set and identify a region of parameters where the optimal performance of the Huber loss is identical to that of the $\ell_2$ loss, offering insights into the use cases of different loss functions.

Genealogical Population-Based Training for Hyperparameter Optimization

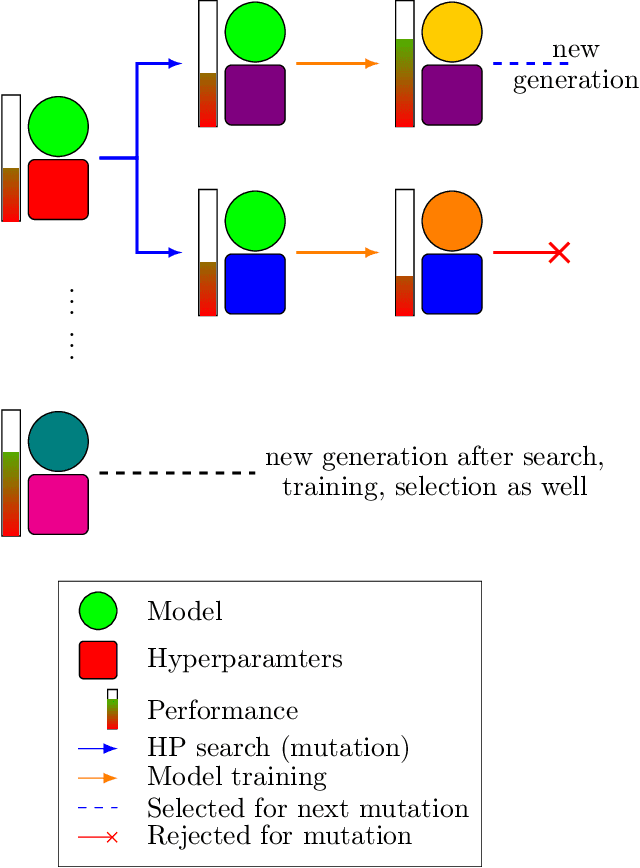
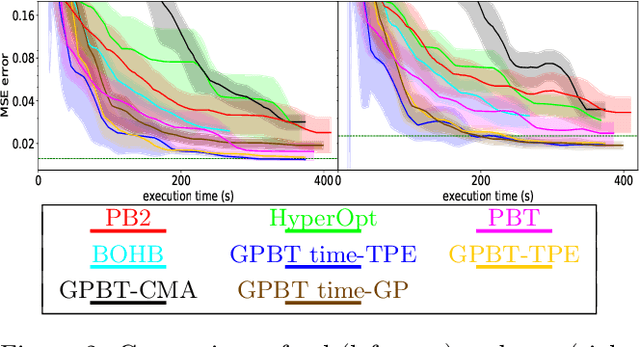
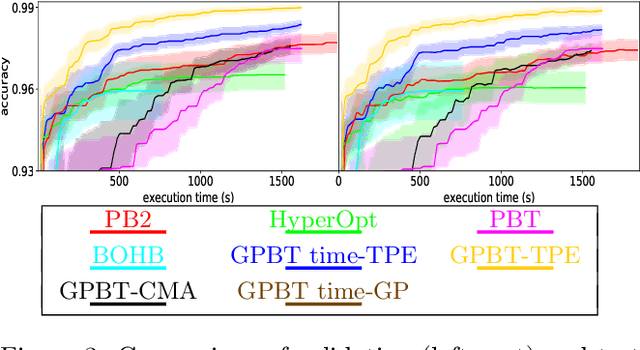
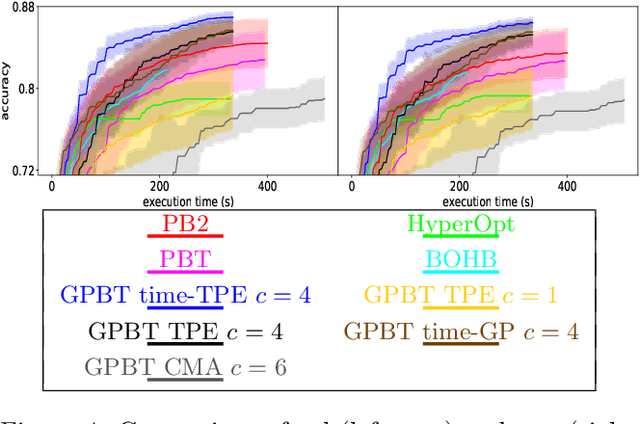
Hyperparameter optimization aims at finding more rapidly and efficiently the best hyperparameters (HPs) of learning models such as neural networks. In this work, we present a new approach called GPBT (Genealogical Population-Based Training), which shares many points with Population-Based Training: our approach outputs a schedule of HPs and updates both weights and HPs in a single run, but brings several novel contributions: the choice of new HPs is made by a modular search algorithm, the search algorithm can search HPs independently for models with different weights and can exploit separately the maximum amount of meaningful information (genealogically-related) from previous HPs evaluations instead of exploiting together all previous HPs evaluations, a variation of early stopping allows a 2-3 fold acceleration at small performance cost. GPBT significantly outperforms all other approaches of HP Optimization, on all supervised learning experiments tested in terms of speed and performances. HPs tuning will become less computationally expensive using our approach, not only in the deep learning field, but potentially for all processes based on iterative optimization.