Flavors of Margin: Implicit Bias of Steepest Descent in Homogeneous Neural Networks

We study the implicit bias of the general family of steepest descent algorithms, which includes gradient descent, sign descent and coordinate descent, in deep homogeneous neural networks. We prove that an algorithm-dependent geometric margin starts increasing once the networks reach perfect training accuracy and characterize the late-stage bias of the algorithms. In particular, we define a generalized notion of stationarity for optimization problems and show that the algorithms progressively reduce a (generalized) Bregman divergence, which quantifies proximity to such stationary points of a margin-maximization problem. We then experimentally zoom into the trajectories of neural networks optimized with various steepest descent algorithms, highlighting connections to the implicit bias of Adam.

On the Geometry of Regularization in Adversarial Training: High-Dimensional Asymptotics and Generalization Bounds

Regularization, whether explicit in terms of a penalty in the loss or implicit in the choice of algorithm, is a cornerstone of modern machine learning. Indeed, controlling the complexity of the model class is particularly important when data is scarce, noisy or contaminated, as it translates a statistical belief on the underlying structure of the data. This work investigates the question of how to choose the regularization norm $\lVert \cdot \rVert$ in the context of high-dimensional adversarial training for binary classification. To this end, we first derive an exact asymptotic description of the robust, regularized empirical risk minimizer for various types of adversarial attacks and regularization norms (including non-$\ell_p$ norms). We complement this analysis with a uniform convergence analysis, deriving bounds on the Rademacher Complexity for this class of problems. Leveraging our theoretical results, we quantitatively characterize the relationship between perturbation size and the optimal choice of $\lVert \cdot \rVert$, confirming the intuition that, in the data scarce regime, the type of regularization becomes increasingly important for adversarial training as perturbations grow in size.

The Price of Implicit Bias in Adversarially Robust Generalization

We study the implicit bias of optimization in robust empirical risk minimization (robust ERM) and its connection with robust generalization. In classification settings under adversarial perturbations with linear models, we study what type of regularization should ideally be applied for a given perturbation set to improve (robust) generalization. We then show that the implicit bias of optimization in robust ERM can significantly affect the robustness of the model and identify two ways this can happen; either through the optimization algorithm or the architecture. We verify our predictions in simulations with synthetic data and experimentally study the importance of implicit bias in robust ERM with deep neural networks.

Attacking Bayes: On the Adversarial Robustness of Bayesian Neural Networks

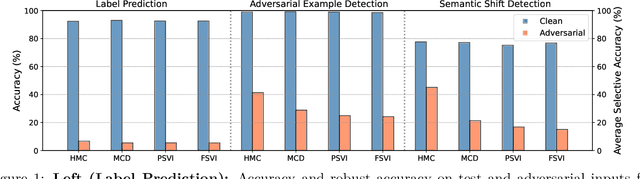
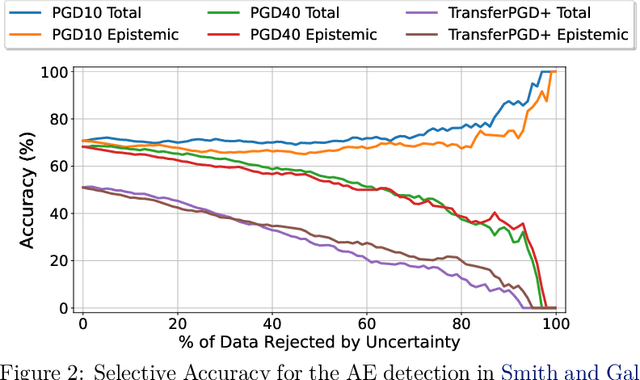
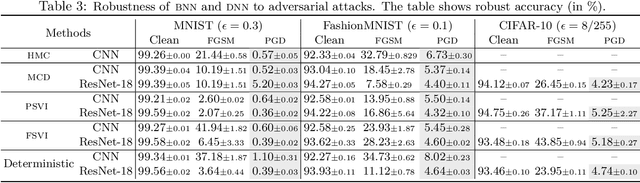
Adversarial examples have been shown to cause neural networks to fail on a wide range of vision and language tasks, but recent work has claimed that Bayesian neural networks (BNNs) are inherently robust to adversarial perturbations. In this work, we examine this claim. To study the adversarial robustness of BNNs, we investigate whether it is possible to successfully break state-of-the-art BNN inference methods and prediction pipelines using even relatively unsophisticated attacks for three tasks: (1) label prediction under the posterior predictive mean, (2) adversarial example detection with Bayesian predictive uncertainty, and (3) semantic shift detection. We find that BNNs trained with state-of-the-art approximate inference methods, and even BNNs trained with Hamiltonian Monte Carlo, are highly susceptible to adversarial attacks. We also identify various conceptual and experimental errors in previous works that claimed inherent adversarial robustness of BNNs and conclusively demonstrate that BNNs and uncertainty-aware Bayesian prediction pipelines are not inherently robust against adversarial attacks.

The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains

Large language models have the ability to generate text that mimics patterns in their inputs. We introduce a simple Markov Chain sequence modeling task in order to study how this in-context learning (ICL) capability emerges. In our setting, each example is sampled from a Markov chain drawn from a prior distribution over Markov chains. Transformers trained on this task form \emph{statistical induction heads} which compute accurate next-token probabilities given the bigram statistics of the context. During the course of training, models pass through multiple phases: after an initial stage in which predictions are uniform, they learn to sub-optimally predict using in-context single-token statistics (unigrams); then, there is a rapid phase transition to the correct in-context bigram solution. We conduct an empirical and theoretical investigation of this multi-phase process, showing how successful learning results from the interaction between the transformer's layers, and uncovering evidence that the presence of the simpler unigram solution may delay formation of the final bigram solution. We examine how learning is affected by varying the prior distribution over Markov chains, and consider the generalization of our in-context learning of Markov chains (ICL-MC) task to $n$-grams for $n > 2$.

On the Robustness of Neural Collapse and the Neural Collapse of Robustness

Neural Collapse refers to the curious phenomenon in the end of training of a neural network, where feature vectors and classification weights converge to a very simple geometrical arrangement (a simplex). While it has been observed empirically in various cases and has been theoretically motivated, its connection with crucial properties of neural networks, like their generalization and robustness, remains unclear. In this work, we study the stability properties of these simplices. We find that the simplex structure disappears under small adversarial attacks, and that perturbed examples "leap" between simplex vertices. We further analyze the geometry of networks that are optimized to be robust against adversarial perturbations of the input, and find that Neural Collapse is a pervasive phenomenon in these cases as well, with clean and perturbed representations forming aligned simplices, and giving rise to a robust simple nearest-neighbor classifier. By studying the propagation of the amount of collapse inside the network, we identify novel properties of both robust and non-robust machine learning models, and show that earlier, unlike later layers maintain reliable simplices on perturbed data.

Kernels, Data & Physics

Lecture notes from the course given by Professor Julia Kempe at the summer school "Statistical physics of Machine Learning" in Les Houches. The notes discuss the so-called NTK approach to problems in machine learning, which consists of gaining an understanding of generally unsolvable problems by finding a tractable kernel formulation. The notes are mainly focused on practical applications such as data distillation and adversarial robustness, examples of inductive bias are also discussed.

A Tale of Two Circuits: Grokking as Competition of Sparse and Dense Subnetworks

Grokking is a phenomenon where a model trained on an algorithmic task first overfits but, then, after a large amount of additional training, undergoes a phase transition to generalize perfectly. We empirically study the internal structure of networks undergoing grokking on the sparse parity task, and find that the grokking phase transition corresponds to the emergence of a sparse subnetwork that dominates model predictions. On an optimization level, we find that this subnetwork arises when a small subset of neurons undergoes rapid norm growth, whereas the other neurons in the network decay slowly in norm. Thus, we suggest that the grokking phase transition can be understood to emerge from competition of two largely distinct subnetworks: a dense one that dominates before the transition and generalizes poorly, and a sparse one that dominates afterwards.

What Can the Neural Tangent Kernel Tell Us About Adversarial Robustness?

The adversarial vulnerability of neural nets, and subsequent techniques to create robust models have attracted significant attention; yet we still lack a full understanding of this phenomenon. Here, we study adversarial examples of trained neural networks through analytical tools afforded by recent theory advances connecting neural networks and kernel methods, namely the Neural Tangent Kernel (NTK), following a growing body of work that leverages the NTK approximation to successfully analyze important deep learning phenomena and design algorithms for new applications. We show how NTKs allow to generate adversarial examples in a ``training-free'' fashion, and demonstrate that they transfer to fool their finite-width neural net counterparts in the ``lazy'' regime. We leverage this connection to provide an alternative view on robust and non-robust features, which have been suggested to underlie the adversarial brittleness of neural nets. Specifically, we define and study features induced by the eigendecomposition of the kernel to better understand the role of robust and non-robust features, the reliance on both for standard classification and the robustness-accuracy trade-off. We find that such features are surprisingly consistent across architectures, and that robust features tend to correspond to the largest eigenvalues of the model, and thus are learned early during training. Our framework allows us to identify and visualize non-robust yet useful features. Finally, we shed light on the robustness mechanism underlying adversarial training of neural nets used in practice: quantifying the evolution of the associated empirical NTK, we demonstrate that its dynamics falls much earlier into the ``lazy'' regime and manifests a much stronger form of the well known bias to prioritize learning features within the top eigenspaces of the kernel, compared to standard training.

Can we achieve robustness from data alone?

Adversarial training and its variants have come to be the prevailing methods to achieve adversarially robust classification using neural networks. However, its increased computational cost together with the significant gap between standard and robust performance hinder progress and beg the question of whether we can do better. In this work, we take a step back and ask: Can models achieve robustness via standard training on a suitably optimized set? To this end, we devise a meta-learning method for robust classification, that optimizes the dataset prior to its deployment in a principled way, and aims to effectively remove the non-robust parts of the data. We cast our optimization method as a multi-step PGD procedure on kernel regression, with a class of kernels that describe infinitely wide neural nets (Neural Tangent Kernels - NTKs). Experiments on MNIST and CIFAR-10 demonstrate that the datasets we produce enjoy very high robustness against PGD attacks, when deployed in both kernel regression classifiers and neural networks. However, this robustness is somewhat fallacious, as alternative attacks manage to fool the models, which we find to be the case for previous similar works in the literature as well. We discuss potential reasons for this and outline further avenues of research.