Scaling Laws and Representation Learning in Simple Hierarchical Languages: Transformers vs. Convolutional Architectures

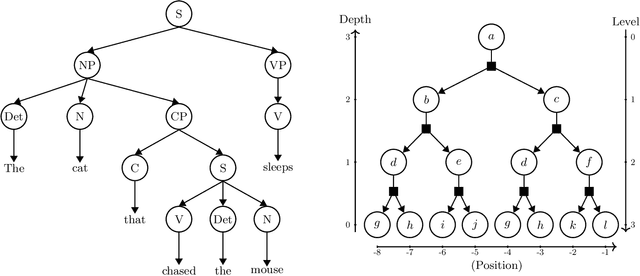
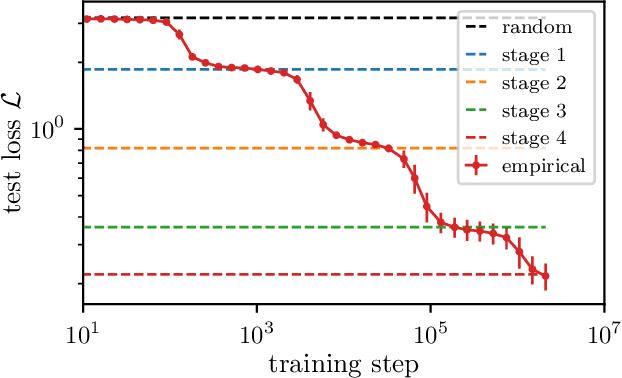
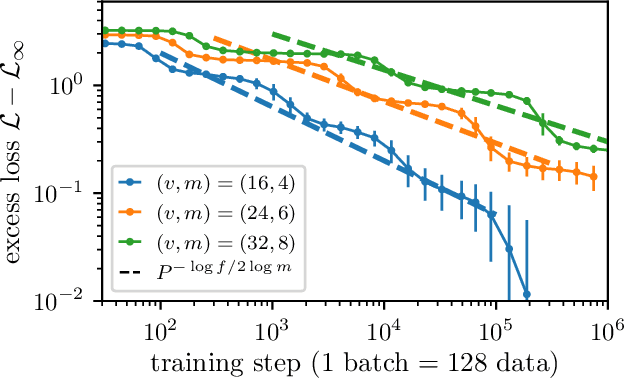
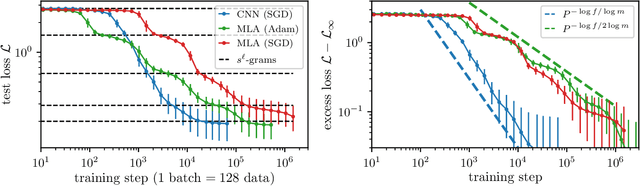
How do neural language models acquire a language's structure when trained for next-token prediction? We address this question by deriving theoretical scaling laws for neural network performance on synthetic datasets generated by the Random Hierarchy Model (RHM) -- an ensemble of probabilistic context-free grammars designed to capture the hierarchical structure of natural language while remaining analytically tractable. Previously, we developed a theory of representation learning based on data correlations that explains how deep learning models capture the hierarchical structure of the data sequentially, one layer at a time. Here, we extend our theoretical framework to account for architectural differences. In particular, we predict and empirically validate that convolutional networks, whose structure aligns with that of the generative process through locality and weight sharing, enjoy a faster scaling of performance compared to transformer models, which rely on global self-attention mechanisms. This finding clarifies the architectural biases underlying neural scaling laws and highlights how representation learning is shaped by the interaction between model architecture and the statistical properties of data.

Learning curves theory for hierarchically compositional data with power-law distributed features

Recent theories suggest that Neural Scaling Laws arise whenever the task is linearly decomposed into power-law distributed units. Alternatively, scaling laws also emerge when data exhibit a hierarchically compositional structure, as is thought to occur in language and images. To unify these views, we consider classification and next-token prediction tasks based on probabilistic context-free grammars -- probabilistic models that generate data via a hierarchy of production rules. For classification, we show that having power-law distributed production rules results in a power-law learning curve with an exponent depending on the rules' distribution and a large multiplicative constant that depends on the hierarchical structure. By contrast, for next-token prediction, the distribution of production rules controls the local details of the learning curve, but not the exponent describing the large-scale behaviour.

How compositional generalization and creativity improve as diffusion models are trained

Natural data is often organized as a hierarchical composition of features. How many samples do generative models need to learn the composition rules, so as to produce a combinatorial number of novel data? What signal in the data is exploited to learn? We investigate these questions both theoretically and empirically. Theoretically, we consider diffusion models trained on simple probabilistic context-free grammars - tree-like graphical models used to represent the structure of data such as language and images. We demonstrate that diffusion models learn compositional rules with the sample complexity required for clustering features with statistically similar context, a process similar to the word2vec algorithm. However, this clustering emerges hierarchically: higher-level, more abstract features associated with longer contexts require more data to be identified. This mechanism leads to a sample complexity that scales polynomially with the said context size. As a result, diffusion models trained on intermediate dataset size generate data coherent up to a certain scale, but that lacks global coherence. We test these predictions in different domains, and find remarkable agreement: both generated texts and images achieve progressively larger coherence lengths as the training time or dataset size grows. We discuss connections between the hierarchical clustering mechanism we introduce here and the renormalization group in physics.

Towards a theory of how the structure of language is acquired by deep neural networks

How much data is required to learn the structure of a language via next-token prediction? We study this question for synthetic datasets generated via a Probabilistic Context-Free Grammar (PCFG) -- a hierarchical generative model that captures the tree-like structure of natural languages. We determine token-token correlations analytically in our model and show that they can be used to build a representation of the grammar's hidden variables, the longer the range the deeper the variable. In addition, a finite training set limits the resolution of correlations to an effective range, whose size grows with that of the training set. As a result, a Language Model trained with increasingly many examples can build a deeper representation of the grammar's structure, thus reaching good performance despite the high dimensionality of the problem. We conjecture that the relationship between training set size and effective range of correlations holds beyond our synthetic datasets. In particular, our conjecture predicts how the scaling law for the test loss behaviour with training set size depends on the length of the context window, which we confirm empirically for a collection of lines from Shakespeare's plays.

How Deep Neural Networks Learn Compositional Data: The Random Hierarchy Model

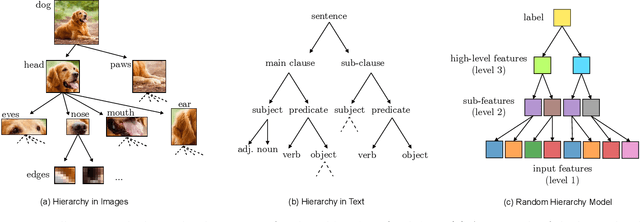
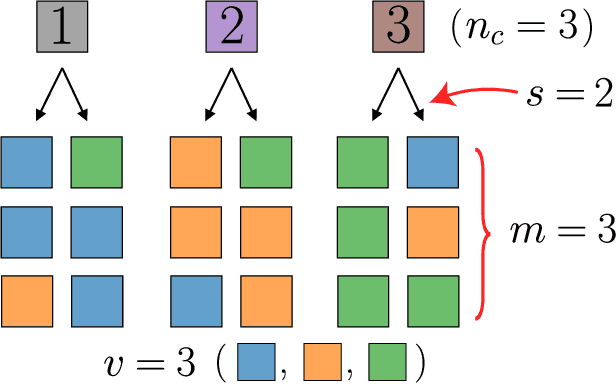
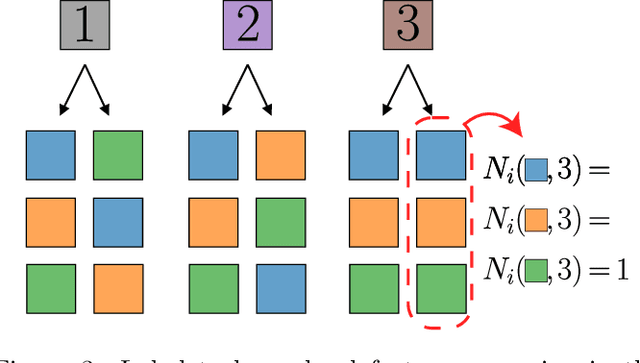
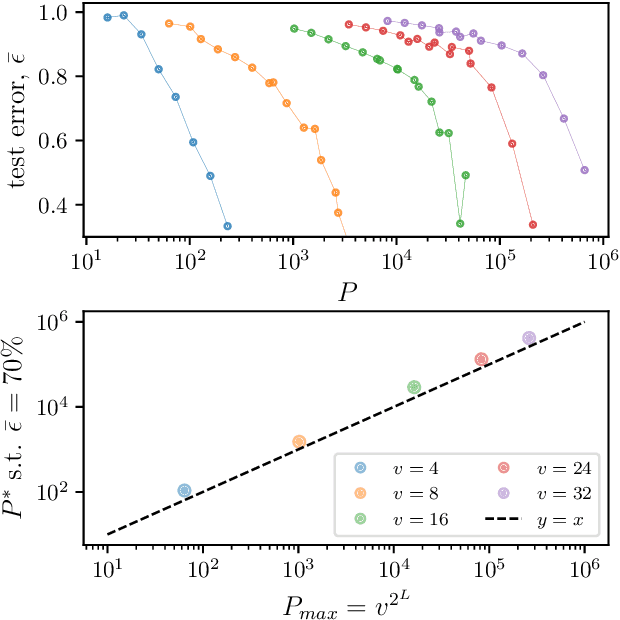
Learning generic high-dimensional tasks is notably hard, as it requires a number of training data exponential in the dimension. Yet, deep convolutional neural networks (CNNs) have shown remarkable success in overcoming this challenge. A popular hypothesis is that learnable tasks are highly structured and that CNNs leverage this structure to build a low-dimensional representation of the data. However, little is known about how much training data they require, and how this number depends on the data structure. This paper answers this question for a simple classification task that seeks to capture relevant aspects of real data: the Random Hierarchy Model. In this model, each of the $n_c$ classes corresponds to $m$ synonymic compositions of high-level features, which are in turn composed of sub-features through an iterative process repeated $L$ times. We find that the number of training data $P^*$ required by deep CNNs to learn this task (i) grows asymptotically as $n_c m^L$, which is only polynomial in the input dimensionality; (ii) coincides with the training set size such that the representation of a trained network becomes invariant to exchanges of synonyms; (iii) corresponds to the number of data at which the correlations between low-level features and classes become detectable. Overall, our results indicate how deep CNNs can overcome the curse of dimensionality by building invariant representations, and provide an estimate of the number of data required to learn a task based on its hierarchically compositional structure.

Kernels, Data & Physics

Lecture notes from the course given by Professor Julia Kempe at the summer school "Statistical physics of Machine Learning" in Les Houches. The notes discuss the so-called NTK approach to problems in machine learning, which consists of gaining an understanding of generally unsolvable problems by finding a tractable kernel formulation. The notes are mainly focused on practical applications such as data distillation and adversarial robustness, examples of inductive bias are also discussed.

How deep convolutional neural networks lose spatial information with training

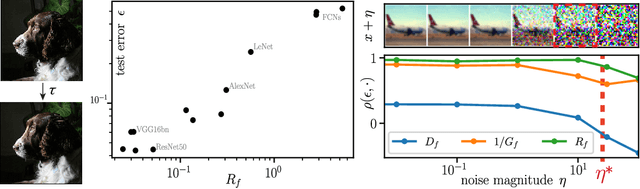
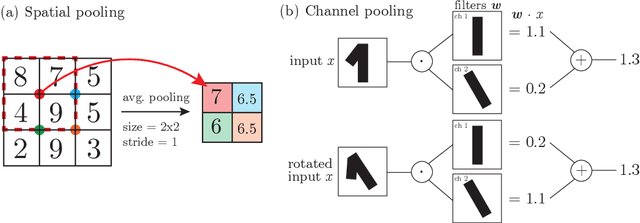
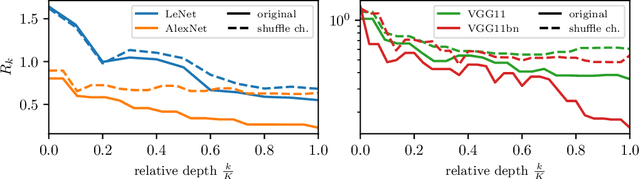
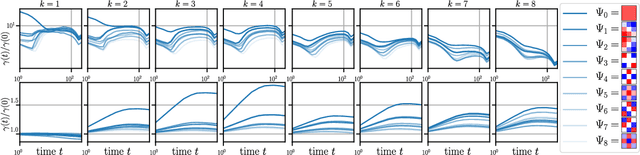
A central question of machine learning is how deep nets manage to learn tasks in high dimensions. An appealing hypothesis is that they achieve this feat by building a representation of the data where information irrelevant to the task is lost. For image datasets, this view is supported by the observation that after (and not before) training, the neural representation becomes less and less sensitive to diffeomorphisms acting on images as the signal propagates through the net. This loss of sensitivity correlates with performance, and surprisingly correlates with a gain of sensitivity to white noise acquired during training. These facts are unexplained, and as we demonstrate still hold when white noise is added to the images of the training set. Here, we (i) show empirically for various architectures that stability to image diffeomorphisms is achieved by spatial pooling in the first half of the net, and by channel pooling in the second half, (ii) introduce a scale-detection task for a simple model of data where pooling is learned during training, which captures all empirical observations above and (iii) compute in this model how stability to diffeomorphisms and noise scale with depth. The scalings are found to depend on the presence of strides in the net architecture. We find that the increased sensitivity to noise is due to the perturbing noise piling up during pooling, after being rectified by ReLU units.

How Wide Convolutional Neural Networks Learn Hierarchical Tasks

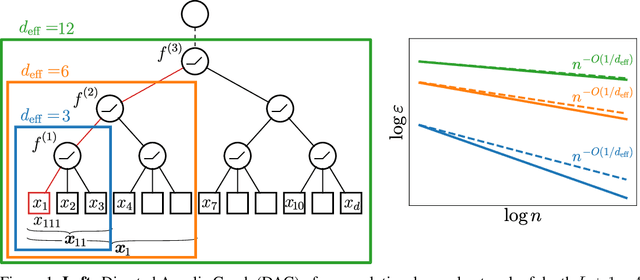
Despite their success, understanding how convolutional neural networks (CNNs) can efficiently learn high-dimensional functions remains a fundamental challenge. A popular belief is that these models harness the compositional and hierarchical structure of natural data such as images. Yet, we lack a quantitative understanding of how such structure affects performances, e.g. the rate of decay of the generalisation error with the number of training samples. In this paper we study deep CNNs in the kernel regime: i) we show that the spectrum of the corresponding kernel and its asymptotics inherit the hierarchical structure of the network; ii) we use generalisation bounds to prove that deep CNNs adapt to the spatial scale of the target function; iii) we illustrate this result by computing the rate of decay of the error in a teacher-student setting, where a deep CNN is trained on the output of another deep CNN with randomly-initialised parameters. We find that if the teacher function depends on certain low-dimensional subsets of the input variables, then the rate is controlled by the effective dimensionality of these subsets. Conversely, if the teacher function depends on the full set of input variables, then the error rate is inversely proportional to the input dimension. Interestingly, this implies that despite their hierarchical structure, the functions generated by deep CNNs are too rich to be efficiently learnable in high dimension.

Learning sparse features can lead to overfitting in neural networks

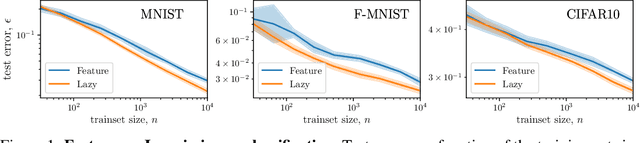
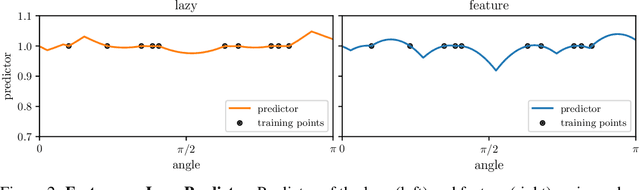
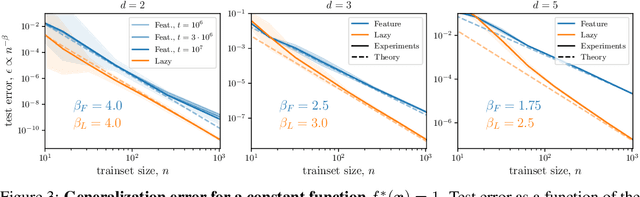
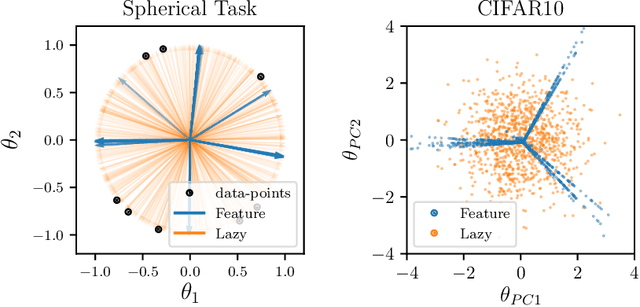
It is widely believed that the success of deep networks lies in their ability to learn a meaningful representation of the features of the data. Yet, understanding when and how this feature learning improves performance remains a challenge: for example, it is beneficial for modern architectures trained to classify images, whereas it is detrimental for fully-connected networks trained for the same task on the same data. Here we propose an explanation for this puzzle, by showing that feature learning can perform worse than lazy training (via random feature kernel or the NTK) as the former can lead to a sparser neural representation. Although sparsity is known to be essential for learning anisotropic data, it is detrimental when the target function is constant or smooth along certain directions of input space. We illustrate this phenomenon in two settings: (i) regression of Gaussian random functions on the d-dimensional unit sphere and (ii) classification of benchmark datasets of images. For (i), we compute the scaling of the generalization error with number of training points, and show that methods that do not learn features generalize better, even when the dimension of the input space is large. For (ii), we show empirically that learning features can indeed lead to sparse and thereby less smooth representations of the image predictors. This fact is plausibly responsible for deteriorating the performance, which is known to be correlated with smoothness along diffeomorphisms.

Locality defeats the curse of dimensionality in convolutional teacher-student scenarios

Convolutional neural networks perform a local and translationally-invariant treatment of the data: quantifying which of these two aspects is central to their success remains a challenge. We study this problem within a teacher-student framework for kernel regression, using `convolutional' kernels inspired by the neural tangent kernel of simple convolutional architectures of given filter size. Using heuristic methods from physics, we find in the ridgeless case that locality is key in determining the learning curve exponent $\beta$ (that relates the test error $\epsilon_t\sim P^{-\beta}$ to the size of the training set $P$), whereas translational invariance is not. In particular, if the filter size of the teacher $t$ is smaller than that of the student $s$, $\beta$ is a function of $s$ only and does not depend on the input dimension. We confirm our predictions on $\beta$ empirically. Theoretically, in some cases (including when teacher and student are equal) it can be shown that this prediction is an upper bound on performance. We conclude by proving, using a natural universality assumption, that performing kernel regression with a ridge that decreases with the size of the training set leads to similar learning curve exponents to those we obtain in the ridgeless case.