MEMOIR: Lifelong Model Editing with Minimal Overwrite and Informed Retention for LLMs

Language models deployed in real-world systems often require post-hoc updates to incorporate new or corrected knowledge. However, editing such models efficiently and reliably - without retraining or forgetting previous information - remains a major challenge. Existing methods for lifelong model editing either compromise generalization, interfere with past edits, or fail to scale to long editing sequences. We propose MEMOIR, a novel scalable framework that injects knowledge through a residual memory, i.e., a dedicated parameter module, while preserving the core capabilities of the pre-trained model. By sparsifying input activations through sample-dependent masks, MEMOIR confines each edit to a distinct subset of the memory parameters, minimizing interference among edits. At inference, it identifies relevant edits by comparing the sparse activation patterns of new queries to those stored during editing. This enables generalization to rephrased queries by activating only the relevant knowledge while suppressing unnecessary memory activation for unrelated prompts. Experiments on question answering, hallucination correction, and out-of-distribution generalization benchmarks across LLaMA-3 and Mistral demonstrate that MEMOIR achieves state-of-the-art performance across reliability, generalization, and locality metrics, scaling to thousands of sequential edits with minimal forgetting.

Bigger Isn't Always Memorizing: Early Stopping Overparameterized Diffusion Models

Diffusion probabilistic models have become a cornerstone of modern generative AI, yet the mechanisms underlying their generalization remain poorly understood. In fact, if these models were perfectly minimizing their training loss, they would just generate data belonging to their training set, i.e., memorize, as empirically found in the overparameterized regime. We revisit this view by showing that, in highly overparameterized diffusion models, generalization in natural data domains is progressively achieved during training before the onset of memorization. Our results, ranging from image to language diffusion models, systematically support the empirical law that memorization time is proportional to the dataset size. Generalization vs. memorization is then best understood as a competition between time scales. We show that this phenomenology is recovered in diffusion models learning a simple probabilistic context-free grammar with random rules, where generalization corresponds to the hierarchical acquisition of deeper grammar rules as training time grows, and the generalization cost of early stopping can be characterized. We summarize these results in a phase diagram. Overall, our results support that a principled early-stopping criterion - scaling with dataset size - can effectively optimize generalization while avoiding memorization, with direct implications for hyperparameter transfer and privacy-sensitive applications.

Scaling Laws and Representation Learning in Simple Hierarchical Languages: Transformers vs. Convolutional Architectures

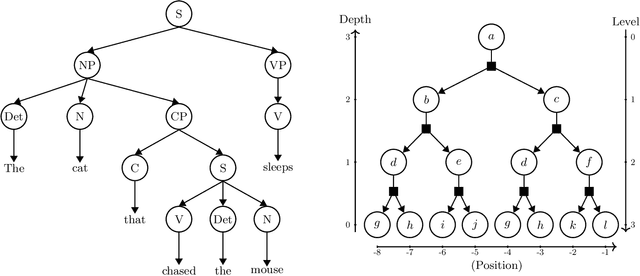
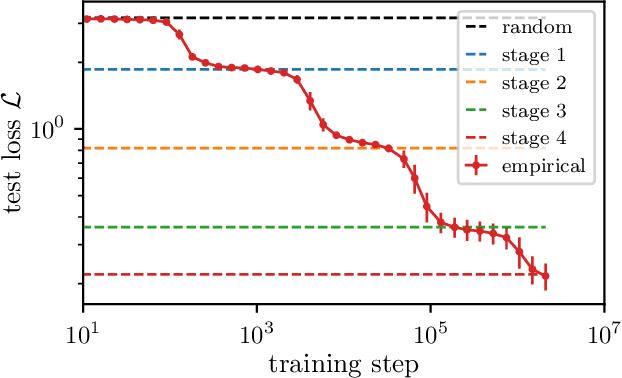
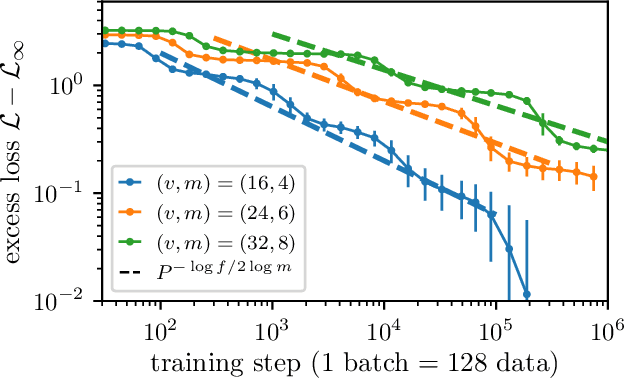
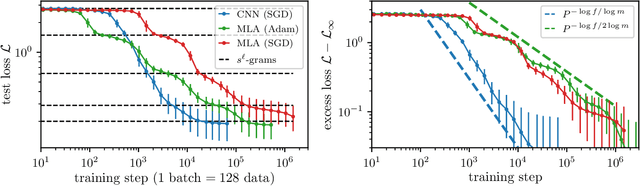
How do neural language models acquire a language's structure when trained for next-token prediction? We address this question by deriving theoretical scaling laws for neural network performance on synthetic datasets generated by the Random Hierarchy Model (RHM) -- an ensemble of probabilistic context-free grammars designed to capture the hierarchical structure of natural language while remaining analytically tractable. Previously, we developed a theory of representation learning based on data correlations that explains how deep learning models capture the hierarchical structure of the data sequentially, one layer at a time. Here, we extend our theoretical framework to account for architectural differences. In particular, we predict and empirically validate that convolutional networks, whose structure aligns with that of the generative process through locality and weight sharing, enjoy a faster scaling of performance compared to transformer models, which rely on global self-attention mechanisms. This finding clarifies the architectural biases underlying neural scaling laws and highlights how representation learning is shaped by the interaction between model architecture and the statistical properties of data.

How compositional generalization and creativity improve as diffusion models are trained

Natural data is often organized as a hierarchical composition of features. How many samples do generative models need to learn the composition rules, so as to produce a combinatorial number of novel data? What signal in the data is exploited to learn? We investigate these questions both theoretically and empirically. Theoretically, we consider diffusion models trained on simple probabilistic context-free grammars - tree-like graphical models used to represent the structure of data such as language and images. We demonstrate that diffusion models learn compositional rules with the sample complexity required for clustering features with statistically similar context, a process similar to the word2vec algorithm. However, this clustering emerges hierarchically: higher-level, more abstract features associated with longer contexts require more data to be identified. This mechanism leads to a sample complexity that scales polynomially with the said context size. As a result, diffusion models trained on intermediate dataset size generate data coherent up to a certain scale, but that lacks global coherence. We test these predictions in different domains, and find remarkable agreement: both generated texts and images achieve progressively larger coherence lengths as the training time or dataset size grows. We discuss connections between the hierarchical clustering mechanism we introduce here and the renormalization group in physics.

LiNeS: Post-training Layer Scaling Prevents Forgetting and Enhances Model Merging

Large pre-trained models exhibit impressive zero-shot performance across diverse tasks, but fine-tuning often leads to catastrophic forgetting, where improvements on a target domain degrade generalization on other tasks. To address this challenge, we introduce LiNeS, Layer-increasing Network Scaling, a post-training editing technique designed to preserve pre-trained generalization while enhancing fine-tuned task performance. LiNeS scales parameter updates linearly based on their layer depth within the network, maintaining shallow layers close to their pre-trained values to preserve general features while allowing deeper layers to retain task-specific representations. We further extend this approach to multi-task model merging scenarios, where layer-wise scaling of merged parameters reduces negative task interference. LiNeS demonstrates significant improvements in both single-task and multi-task settings across various benchmarks in vision and natural language processing. It mitigates forgetting, enhances out-of-distribution generalization, integrates seamlessly with existing multi-task model merging baselines improving their performance across benchmarks and model sizes, and can boost generalization when merging LLM policies aligned with different rewards via RLHF. Importantly, our method is simple to implement and complementary to many existing techniques.

Probing the Latent Hierarchical Structure of Data via Diffusion Models

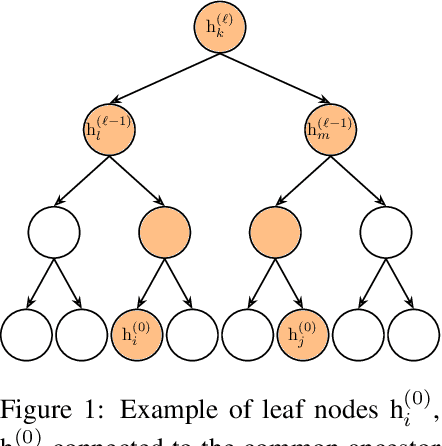
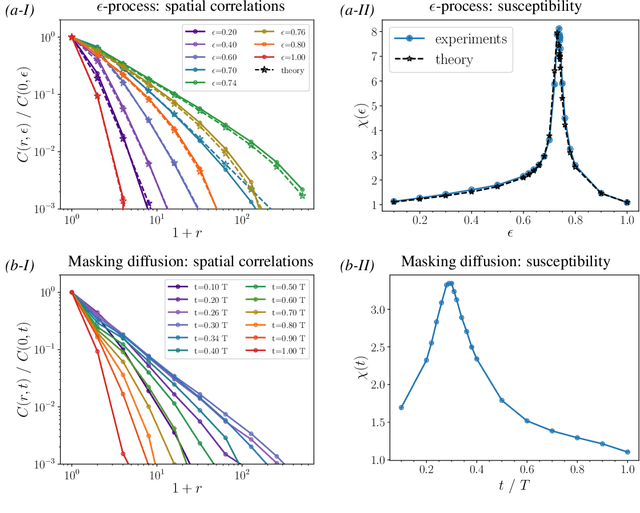
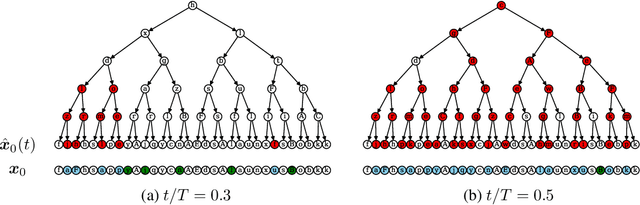
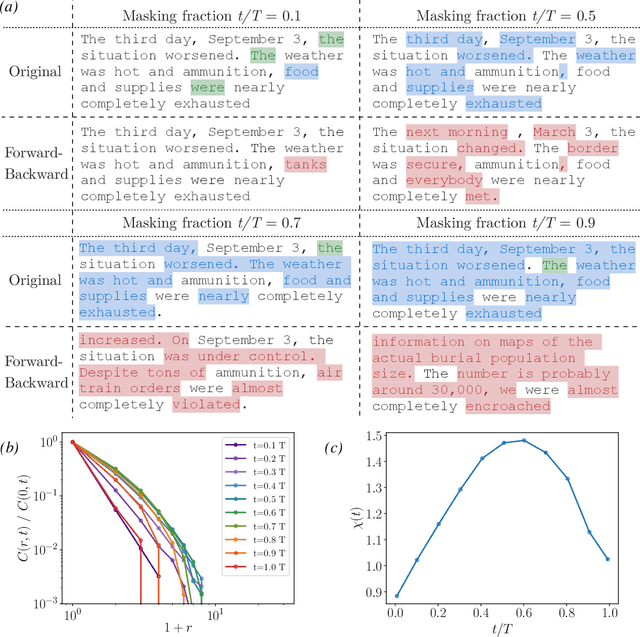
High-dimensional data must be highly structured to be learnable. Although the compositional and hierarchical nature of data is often put forward to explain learnability, quantitative measurements establishing these properties are scarce. Likewise, accessing the latent variables underlying such a data structure remains a challenge. In this work, we show that forward-backward experiments in diffusion-based models, where data is noised and then denoised to generate new samples, are a promising tool to probe the latent structure of data. We predict in simple hierarchical models that, in this process, changes in data occur by correlated chunks, with a length scale that diverges at a noise level where a phase transition is known to take place. Remarkably, we confirm this prediction in both text and image datasets using state-of-the-art diffusion models. Our results show how latent variable changes manifest in the data and establish how to measure these effects in real data using diffusion models.

Multi-Modal Hallucination Control by Visual Information Grounding

Generative Vision-Language Models (VLMs) are prone to generate plausible-sounding textual answers that, however, are not always grounded in the input image. We investigate this phenomenon, usually referred to as "hallucination" and show that it stems from an excessive reliance on the language prior. In particular, we show that as more tokens are generated, the reliance on the visual prompt decreases, and this behavior strongly correlates with the emergence of hallucinations. To reduce hallucinations, we introduce Multi-Modal Mutual-Information Decoding (M3ID), a new sampling method for prompt amplification. M3ID amplifies the influence of the reference image over the language prior, hence favoring the generation of tokens with higher mutual information with the visual prompt. M3ID can be applied to any pre-trained autoregressive VLM at inference time without necessitating further training and with minimal computational overhead. If training is an option, we show that M3ID can be paired with Direct Preference Optimization (DPO) to improve the model's reliance on the prompt image without requiring any labels. Our empirical findings show that our algorithms maintain the fluency and linguistic capabilities of pre-trained VLMs while reducing hallucinations by mitigating visually ungrounded answers. Specifically, for the LLaVA 13B model, M3ID and M3ID+DPO reduce the percentage of hallucinated objects in captioning tasks by 25% and 28%, respectively, and improve the accuracy on VQA benchmarks such as POPE by 21% and 24%.

A Phase Transition in Diffusion Models Reveals the Hierarchical Nature of Data

Understanding the structure of real data is paramount in advancing modern deep-learning methodologies. Natural data such as images are believed to be composed of features organised in a hierarchical and combinatorial manner, which neural networks capture during learning. Recent advancements show that diffusion models can generate high-quality images, hinting at their ability to capture this underlying structure. We study this phenomenon in a hierarchical generative model of data. We find that the backward diffusion process acting after a time $t$ is governed by a phase transition at some threshold time, where the probability of reconstructing high-level features, like the class of an image, suddenly drops. Instead, the reconstruction of low-level features, such as specific details of an image, evolves smoothly across the whole diffusion process. This result implies that at times beyond the transition, the class has changed but the generated sample may still be composed of low-level elements of the initial image. We validate these theoretical insights through numerical experiments on class-unconditional ImageNet diffusion models. Our analysis characterises the relationship between time and scale in diffusion models and puts forward generative models as powerful tools to model combinatorial data properties.

How Deep Neural Networks Learn Compositional Data: The Random Hierarchy Model

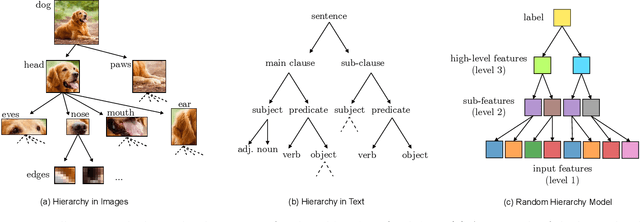
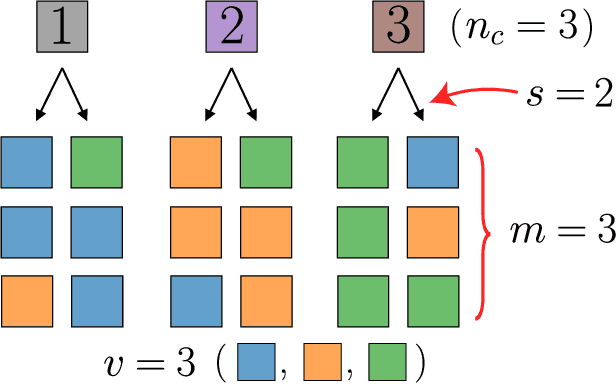
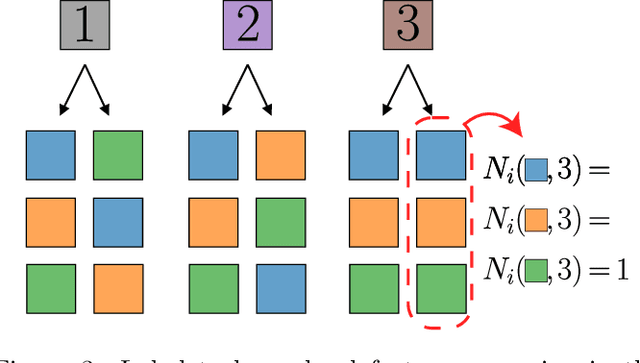
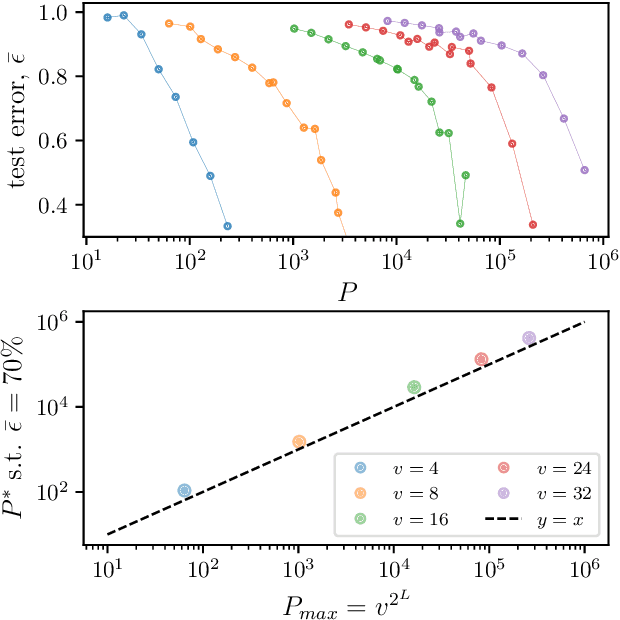
Learning generic high-dimensional tasks is notably hard, as it requires a number of training data exponential in the dimension. Yet, deep convolutional neural networks (CNNs) have shown remarkable success in overcoming this challenge. A popular hypothesis is that learnable tasks are highly structured and that CNNs leverage this structure to build a low-dimensional representation of the data. However, little is known about how much training data they require, and how this number depends on the data structure. This paper answers this question for a simple classification task that seeks to capture relevant aspects of real data: the Random Hierarchy Model. In this model, each of the $n_c$ classes corresponds to $m$ synonymic compositions of high-level features, which are in turn composed of sub-features through an iterative process repeated $L$ times. We find that the number of training data $P^*$ required by deep CNNs to learn this task (i) grows asymptotically as $n_c m^L$, which is only polynomial in the input dimensionality; (ii) coincides with the training set size such that the representation of a trained network becomes invariant to exchanges of synonyms; (iii) corresponds to the number of data at which the correlations between low-level features and classes become detectable. Overall, our results indicate how deep CNNs can overcome the curse of dimensionality by building invariant representations, and provide an estimate of the number of data required to learn a task based on its hierarchically compositional structure.

Task Arithmetic in the Tangent Space: Improved Editing of Pre-Trained Models

Task arithmetic has recently emerged as a cost-effective and scalable approach to edit pre-trained models directly in weight space: By adding the fine-tuned weights of different tasks, the model's performance can be improved on these tasks, while negating them leads to task forgetting. Yet, our understanding of the effectiveness of task arithmetic and its underlying principles remains limited. We present a comprehensive study of task arithmetic in vision-language models and show that weight disentanglement is the crucial factor that makes it effective. This property arises during pre-training and manifests when distinct directions in weight space govern separate, localized regions in function space associated with the tasks. Notably, we show that fine-tuning models in their tangent space by linearizing them amplifies weight disentanglement. This leads to substantial performance improvements across multiple task arithmetic benchmarks and diverse models. Building on these findings, we provide theoretical and empirical analyses of the neural tangent kernel (NTK) of these models and establish a compelling link between task arithmetic and the spatial localization of the NTK eigenfunctions. Overall, our work uncovers novel insights into the fundamental mechanisms of task arithmetic and offers a more reliable and effective approach to edit pre-trained models through the NTK linearization.