How Deep Neural Networks Learn Compositional Data: The Random Hierarchy Model

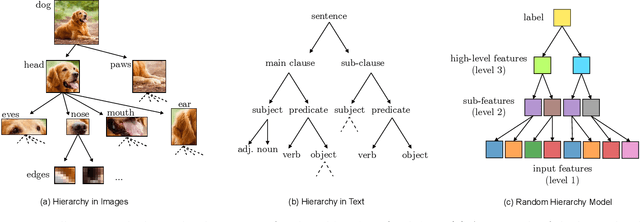
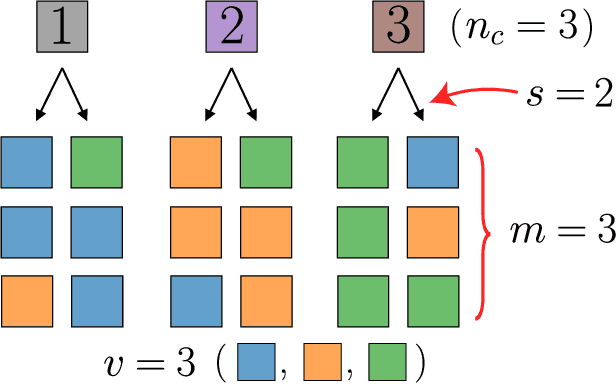
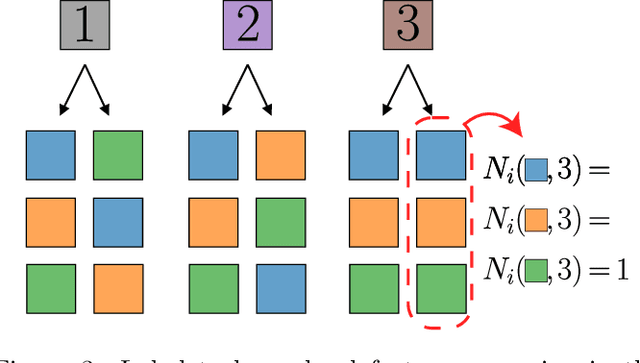
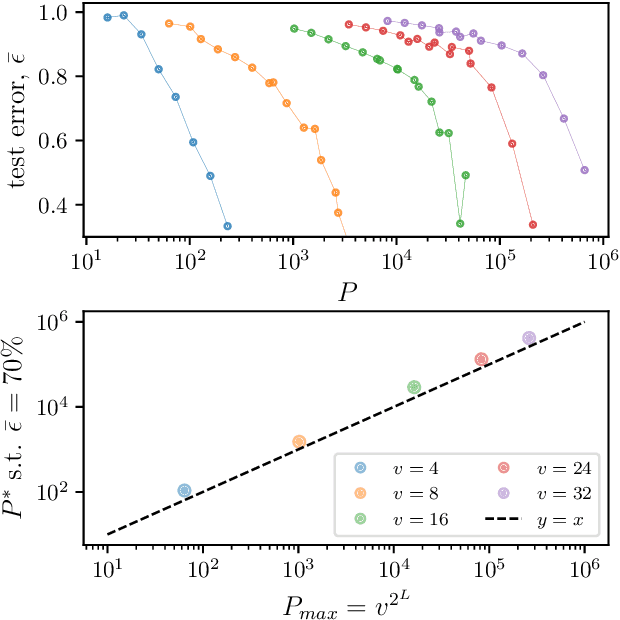
Learning generic high-dimensional tasks is notably hard, as it requires a number of training data exponential in the dimension. Yet, deep convolutional neural networks (CNNs) have shown remarkable success in overcoming this challenge. A popular hypothesis is that learnable tasks are highly structured and that CNNs leverage this structure to build a low-dimensional representation of the data. However, little is known about how much training data they require, and how this number depends on the data structure. This paper answers this question for a simple classification task that seeks to capture relevant aspects of real data: the Random Hierarchy Model. In this model, each of the $n_c$ classes corresponds to $m$ synonymic compositions of high-level features, which are in turn composed of sub-features through an iterative process repeated $L$ times. We find that the number of training data $P^*$ required by deep CNNs to learn this task (i) grows asymptotically as $n_c m^L$, which is only polynomial in the input dimensionality; (ii) coincides with the training set size such that the representation of a trained network becomes invariant to exchanges of synonyms; (iii) corresponds to the number of data at which the correlations between low-level features and classes become detectable. Overall, our results indicate how deep CNNs can overcome the curse of dimensionality by building invariant representations, and provide an estimate of the number of data required to learn a task based on its hierarchically compositional structure.

How deep convolutional neural networks lose spatial information with training

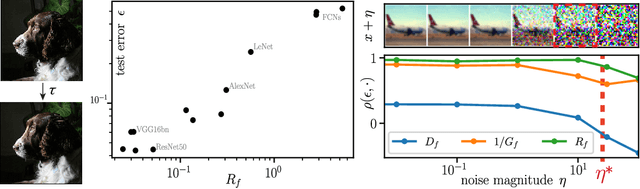
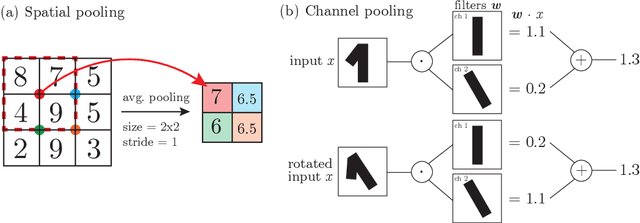
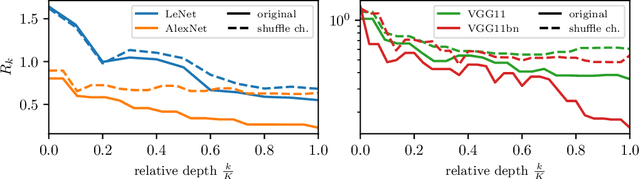
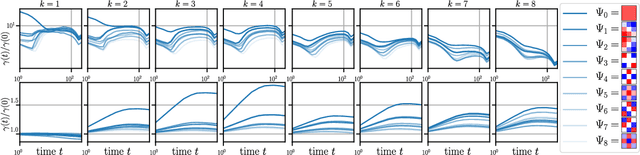
A central question of machine learning is how deep nets manage to learn tasks in high dimensions. An appealing hypothesis is that they achieve this feat by building a representation of the data where information irrelevant to the task is lost. For image datasets, this view is supported by the observation that after (and not before) training, the neural representation becomes less and less sensitive to diffeomorphisms acting on images as the signal propagates through the net. This loss of sensitivity correlates with performance, and surprisingly correlates with a gain of sensitivity to white noise acquired during training. These facts are unexplained, and as we demonstrate still hold when white noise is added to the images of the training set. Here, we (i) show empirically for various architectures that stability to image diffeomorphisms is achieved by spatial pooling in the first half of the net, and by channel pooling in the second half, (ii) introduce a scale-detection task for a simple model of data where pooling is learned during training, which captures all empirical observations above and (iii) compute in this model how stability to diffeomorphisms and noise scale with depth. The scalings are found to depend on the presence of strides in the net architecture. We find that the increased sensitivity to noise is due to the perturbing noise piling up during pooling, after being rectified by ReLU units.

Failure and success of the spectral bias prediction for Kernel Ridge Regression: the case of low-dimensional data

Recently, several theories including the replica method made predictions for the generalization error of Kernel Ridge Regression. In some regimes, they predict that the method has a `spectral bias': decomposing the true function $f^*$ on the eigenbasis of the kernel, it fits well the coefficients associated with the O(P) largest eigenvalues, where $P$ is the size of the training set. This prediction works very well on benchmark data sets such as images, yet the assumptions these approaches make on the data are never satisfied in practice. To clarify when the spectral bias prediction holds, we first focus on a one-dimensional model where rigorous results are obtained and then use scaling arguments to generalize and test our findings in higher dimensions. Our predictions include the classification case $f(x)=$sign$(x_1)$ with a data distribution that vanishes at the decision boundary $p(x)\sim x_1^{\chi}$. For $\chi>0$ and a Laplace kernel, we find that (i) there exists a cross-over ridge $\lambda^*_{d,\chi}(P)\sim P^{-\frac{1}{d+\chi}}$ such that for $\lambda\gg \lambda^*_{d,\chi}(P)$, the replica method applies, but not for $\lambda\ll\lambda^*_{d,\chi}(P)$, (ii) in the ridge-less case, spectral bias predicts the correct training curve exponent only in the limit $d\rightarrow\infty$.