How Wide Convolutional Neural Networks Learn Hierarchical Tasks

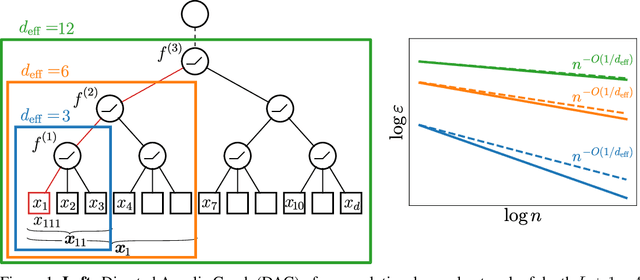
Despite their success, understanding how convolutional neural networks (CNNs) can efficiently learn high-dimensional functions remains a fundamental challenge. A popular belief is that these models harness the compositional and hierarchical structure of natural data such as images. Yet, we lack a quantitative understanding of how such structure affects performances, e.g. the rate of decay of the generalisation error with the number of training samples. In this paper we study deep CNNs in the kernel regime: i) we show that the spectrum of the corresponding kernel and its asymptotics inherit the hierarchical structure of the network; ii) we use generalisation bounds to prove that deep CNNs adapt to the spatial scale of the target function; iii) we illustrate this result by computing the rate of decay of the error in a teacher-student setting, where a deep CNN is trained on the output of another deep CNN with randomly-initialised parameters. We find that if the teacher function depends on certain low-dimensional subsets of the input variables, then the rate is controlled by the effective dimensionality of these subsets. Conversely, if the teacher function depends on the full set of input variables, then the error rate is inversely proportional to the input dimension. Interestingly, this implies that despite their hierarchical structure, the functions generated by deep CNNs are too rich to be efficiently learnable in high dimension.