Learning sparse features can lead to overfitting in neural networks
Paper and Code
Jun 24, 2022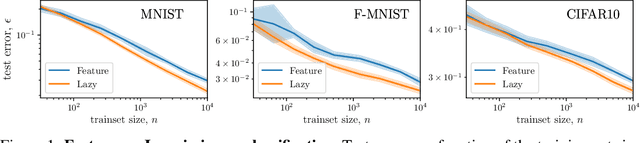
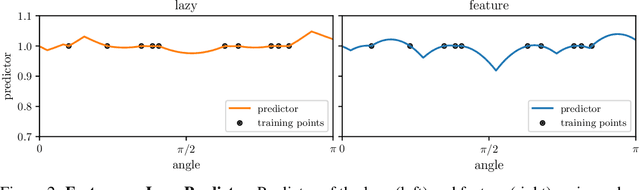
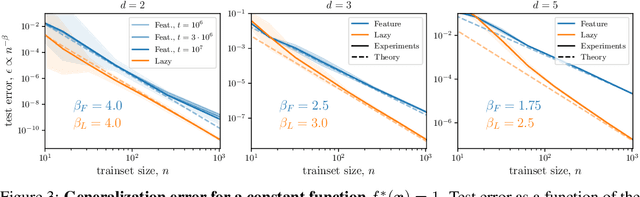
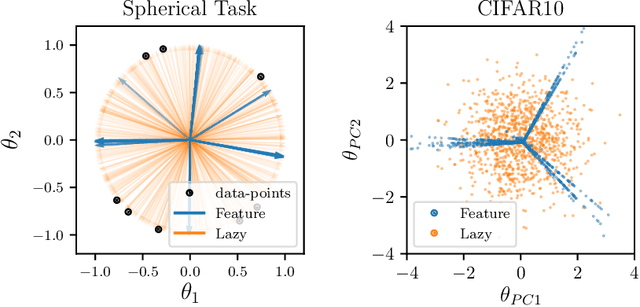
It is widely believed that the success of deep networks lies in their ability to learn a meaningful representation of the features of the data. Yet, understanding when and how this feature learning improves performance remains a challenge: for example, it is beneficial for modern architectures trained to classify images, whereas it is detrimental for fully-connected networks trained for the same task on the same data. Here we propose an explanation for this puzzle, by showing that feature learning can perform worse than lazy training (via random feature kernel or the NTK) as the former can lead to a sparser neural representation. Although sparsity is known to be essential for learning anisotropic data, it is detrimental when the target function is constant or smooth along certain directions of input space. We illustrate this phenomenon in two settings: (i) regression of Gaussian random functions on the d-dimensional unit sphere and (ii) classification of benchmark datasets of images. For (i), we compute the scaling of the generalization error with number of training points, and show that methods that do not learn features generalize better, even when the dimension of the input space is large. For (ii), we show empirically that learning features can indeed lead to sparse and thereby less smooth representations of the image predictors. This fact is plausibly responsible for deteriorating the performance, which is known to be correlated with smoothness along diffeomorphisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge