Optimal Spectral Transitions in High-Dimensional Multi-Index Models

We consider the problem of how many samples from a Gaussian multi-index model are required to weakly reconstruct the relevant index subspace. Despite its increasing popularity as a testbed for investigating the computational complexity of neural networks, results beyond the single-index setting remain elusive. In this work, we introduce spectral algorithms based on the linearization of a message passing scheme tailored to this problem. Our main contribution is to show that the proposed methods achieve the optimal reconstruction threshold. Leveraging a high-dimensional characterization of the algorithms, we show that above the critical threshold the leading eigenvector correlates with the relevant index subspace, a phenomenon reminiscent of the Baik-Ben Arous-Peche (BBP) transition in spiked models arising in random matrix theory. Supported by numerical experiments and a rigorous theoretical framework, our work bridges critical gaps in the computational limits of weak learnability in multi-index model.

Fundamental limits of Non-Linear Low-Rank Matrix Estimation

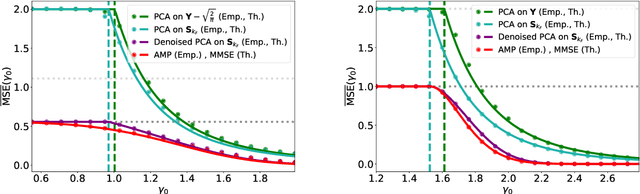
We consider the task of estimating a low-rank matrix from non-linear and noisy observations. We prove a strong universality result showing that Bayes-optimal performances are characterized by an equivalent Gaussian model with an effective prior, whose parameters are entirely determined by an expansion of the non-linear function. In particular, we show that to reconstruct the signal accurately, one requires a signal-to-noise ratio growing as $N^{\frac 12 (1-1/k_F)}$, where $k_F$ is the first non-zero Fisher information coefficient of the function. We provide asymptotic characterization for the minimal achievable mean squared error (MMSE) and an approximate message-passing algorithm that reaches the MMSE under conditions analogous to the linear version of the problem. We also provide asymptotic errors achieved by methods such as principal component analysis combined with Bayesian denoising, and compare them with Bayes-optimal MMSE.

Spectral Phase Transition and Optimal PCA in Block-Structured Spiked models

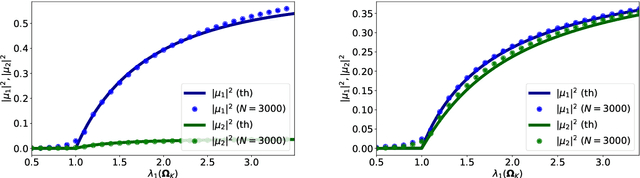
We discuss the inhomogeneous spiked Wigner model, a theoretical framework recently introduced to study structured noise in various learning scenarios, through the prism of random matrix theory, with a specific focus on its spectral properties. Our primary objective is to find an optimal spectral method and to extend the celebrated \cite{BBP} (BBP) phase transition criterion -- well-known in the homogeneous case -- to our inhomogeneous, block-structured, Wigner model. We provide a thorough rigorous analysis of a transformed matrix and show that the transition for the appearance of 1) an outlier outside the bulk of the limiting spectral distribution and 2) a positive overlap between the associated eigenvector and the signal, occurs precisely at the optimal threshold, making the proposed spectral method optimal within the class of iterative methods for the inhomogeneous Wigner problem.