Improved Representation Learning Through Tensorized Autoencoders

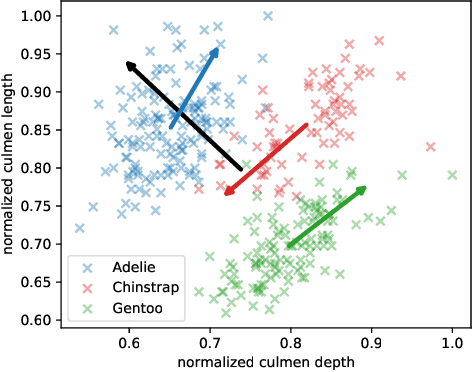
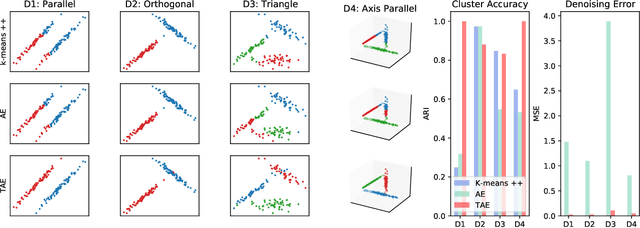
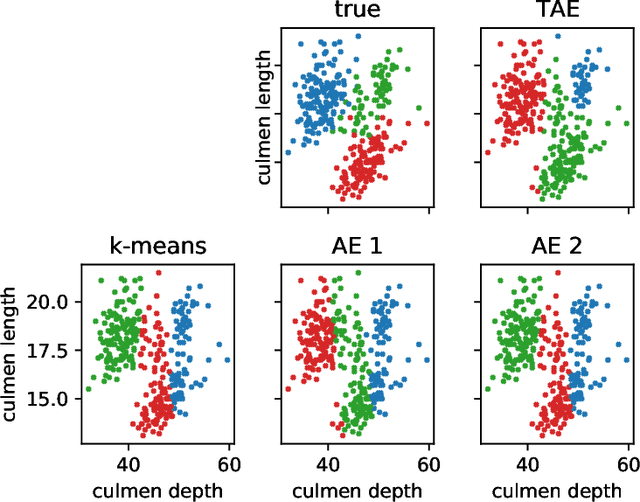
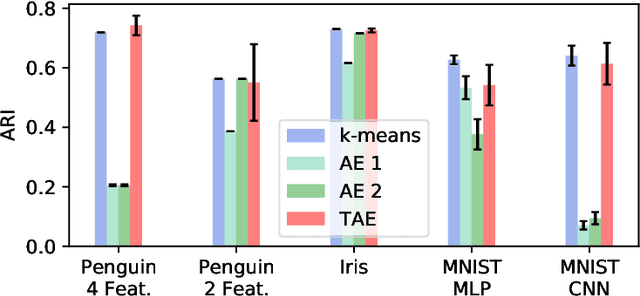
The central question in representation learning is what constitutes a good or meaningful representation. In this work we argue that if we consider data with inherent cluster structures, where clusters can be characterized through different means and covariances, those data structures should be represented in the embedding as well. While Autoencoders (AE) are widely used in practice for unsupervised representation learning, they do not fulfil the above condition on the embedding as they obtain a single representation of the data. To overcome this we propose a meta-algorithm that can be used to extend an arbitrary AE architecture to a tensorized version (TAE) that allows for learning cluster-specific embeddings while simultaneously learning the cluster assignment. For the linear setting we prove that TAE can recover the principle components of the different clusters in contrast to principle component of the entire data recovered by a standard AE. We validated this on planted models and for general, non-linear and convolutional AEs we empirically illustrate that tensorizing the AE is beneficial in clustering and de-noising tasks.

On the Influence of Enforcing Model Identifiability on Learning dynamics of Gaussian Mixture Models

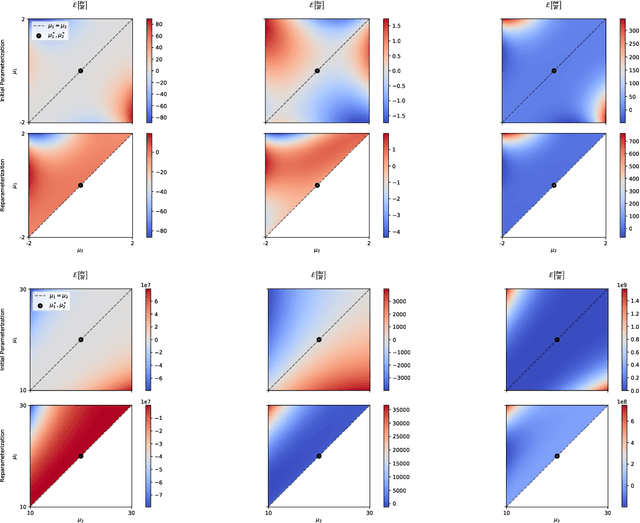
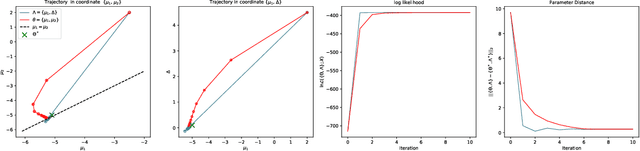
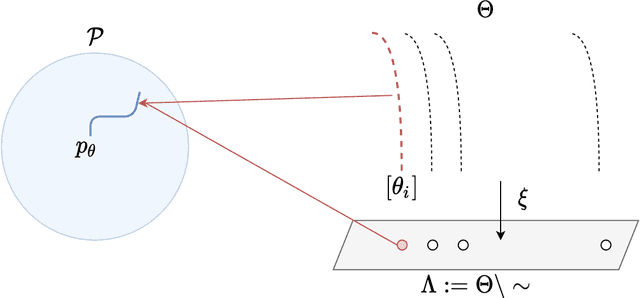
A common way to learn and analyze statistical models is to consider operations in the model parameter space. But what happens if we optimize in the parameter space and there is no one-to-one mapping between the parameter space and the underlying statistical model space? Such cases frequently occur for hierarchical models which include statistical mixtures or stochastic neural networks, and these models are said to be singular. Singular models reveal several important and well-studied problems in machine learning like the decrease in convergence speed of learning trajectories due to attractor behaviors. In this work, we propose a relative reparameterization technique of the parameter space, which yields a general method for extracting regular submodels from singular models. Our method enforces model identifiability during training and we study the learning dynamics for gradient descent and expectation maximization for Gaussian Mixture Models (GMMs) under relative parameterization, showing faster experimental convergence and a improved manifold shape of the dynamics around the singularity. Extending the analysis beyond GMMs, we furthermore analyze the Fisher information matrix under relative reparameterization and its influence on the generalization error, and show how the method can be applied to more complex models like deep neural networks.

Learning Theory Can (Sometimes) Explain Generalisation in Graph Neural Networks

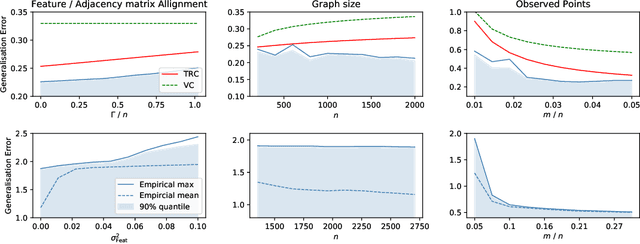
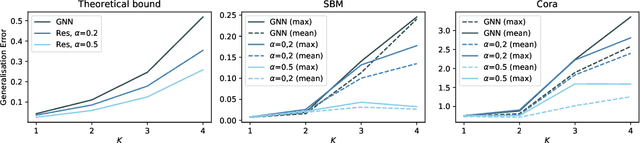
In recent years, several results in the supervised learning setting suggested that classical statistical learning-theoretic measures, such as VC dimension, do not adequately explain the performance of deep learning models which prompted a slew of work in the infinite-width and iteration regimes. However, there is little theoretical explanation for the success of neural networks beyond the supervised setting. In this paper we argue that, under some distributional assumptions, classical learning-theoretic measures can sufficiently explain generalization for graph neural networks in the transductive setting. In particular, we provide a rigorous analysis of the performance of neural networks in the context of transductive inference, specifically by analysing the generalisation properties of graph convolutional networks for the problem of node classification. While VC Dimension does result in trivial generalisation error bounds in this setting as well, we show that transductive Rademacher complexity can explain the generalisation properties of graph convolutional networks for stochastic block models. We further use the generalisation error bounds based on transductive Rademacher complexity to demonstrate the role of graph convolutions and network architectures in achieving smaller generalisation error and provide insights into when the graph structure can help in learning. The findings of this paper could re-new the interest in studying generalisation in neural networks in terms of learning-theoretic measures, albeit in specific problems.

Towards Modeling and Resolving Singular Parameter Spaces using Stratifolds

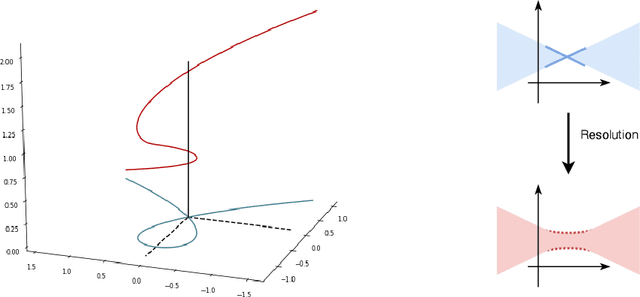
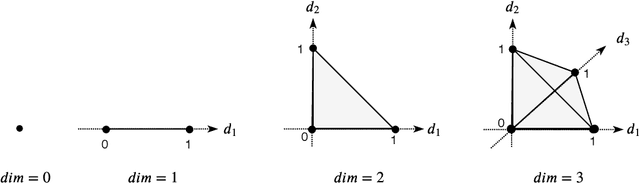
When analyzing parametric statistical models, a useful approach consists in modeling geometrically the parameter space. However, even for very simple and commonly used hierarchical models like statistical mixtures or stochastic deep neural networks, the smoothness assumption of manifolds is violated at singular points which exhibit non-smooth neighborhoods in the parameter space. These singular models have been analyzed in the context of learning dynamics, where singularities can act as attractors on the learning trajectory and, therefore, negatively influence the convergence speed of models. We propose a general approach to circumvent the problem arising from singularities by using stratifolds, a concept from algebraic topology, to formally model singular parameter spaces. We use the property that specific stratifolds are equipped with a resolution method to construct a smooth manifold approximation of the singular space. We empirically show that using (natural) gradient descent on the smooth manifold approximation instead of the singular space allows us to avoid the attractor behavior and therefore improve the convergence speed in learning.

Near-Optimal Comparison Based Clustering

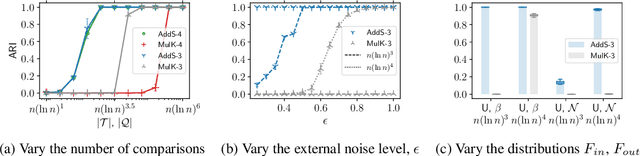
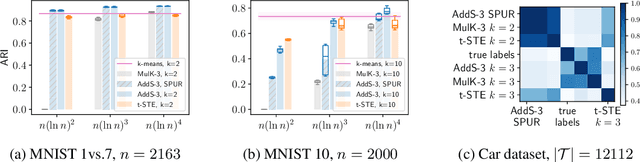
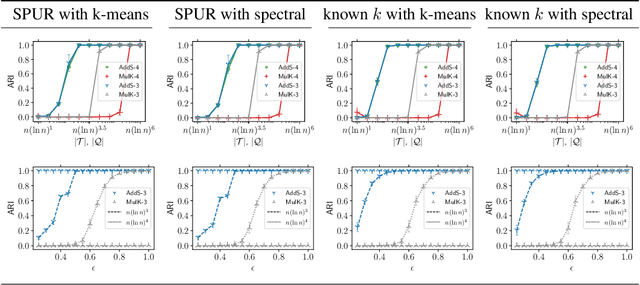
The goal of clustering is to group similar objects into meaningful partitions. This process is well understood when an explicit similarity measure between the objects is given. However, far less is known when this information is not readily available and, instead, one only observes ordinal comparisons such as "object i is more similar to j than to k." In this paper, we tackle this problem using a two-step procedure: we estimate a pairwise similarity matrix from the comparisons before using a clustering method based on semi-definite programming (SDP). We theoretically show that our approach can exactly recover a planted clustering using a near-optimal number of passive comparisons. We empirically validate our theoretical findings and demonstrate the good behaviour of our method on real data.