On the Impact of Output Perturbation on Fairness in Binary Linear Classification

We theoretically study how differential privacy interacts with both individual and group fairness in binary linear classification. More precisely, we focus on the output perturbation mechanism, a classic approach in privacy-preserving machine learning. We derive high-probability bounds on the level of individual and group fairness that the perturbed models can achieve compared to the original model. Hence, for individual fairness, we prove that the impact of output perturbation on the level of fairness is bounded but grows with the dimension of the model. For group fairness, we show that this impact is determined by the distribution of so-called angular margins, that is signed margins of the non-private model re-scaled by the norm of each example.

A Revenue Function for Comparison-Based Hierarchical Clustering

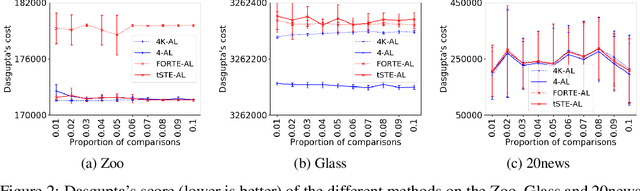
Comparison-based learning addresses the problem of learning when, instead of explicit features or pairwise similarities, one only has access to comparisons of the form: \emph{Object $A$ is more similar to $B$ than to $C$.} Recently, it has been shown that, in Hierarchical Clustering, single and complete linkage can be directly implemented using only such comparisons while several algorithms have been proposed to emulate the behaviour of average linkage. Hence, finding hierarchies (or dendrograms) using only comparisons is a well understood problem. However, evaluating their meaningfulness when no ground-truth nor explicit similarities are available remains an open question. In this paper, we bridge this gap by proposing a new revenue function that allows one to measure the goodness of dendrograms using only comparisons. We show that this function is closely related to Dasgupta's cost for hierarchical clustering that uses pairwise similarities. On the theoretical side, we use the proposed revenue function to resolve the open problem of whether one can approximately recover a latent hierarchy using few triplet comparisons. On the practical side, we present principled algorithms for comparison-based hierarchical clustering based on the maximisation of the revenue and we empirically compare them with existing methods.

Fairness Certificates for Differentially Private Classification

In this work, we theoretically study the impact of differential privacy on fairness in binary classification. We prove that, given a class of models, popular group fairness measures are pointwise Lipschitz-continuous with respect to the parameters of the model. This result is a consequence of a more general statement on the probability that a decision function makes a negative prediction conditioned on an arbitrary event (such as membership to a sensitive group), which may be of independent interest. We use the aforementioned Lipschitz property to prove a high probability bound showing that, given enough examples, the fairness level of private models is close to the one of their non-private counterparts.

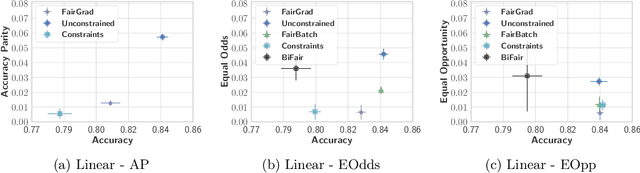
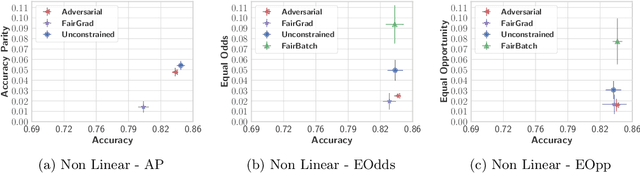
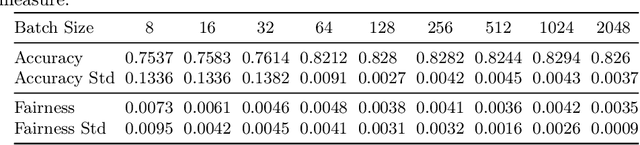
FairGrad: Fairness Aware Gradient Descent

We tackle the problem of group fairness in classification, where the objective is to learn models that do not unjustly discriminate against subgroups of the population. Most existing approaches are limited to simple binary tasks or involve difficult to implement training mechanisms. This reduces their practical applicability. In this paper, we propose FairGrad, a method to enforce fairness based on a reweighting scheme that iteratively learns group specific weights based on whether they are advantaged or not. FairGrad is easy to implement and can accommodate various standard fairness definitions. Furthermore, we show that it is comparable to standard baselines over various datasets including ones used in natural language processing and computer vision.

Near-Optimal Comparison Based Clustering

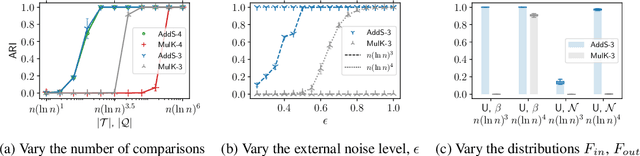
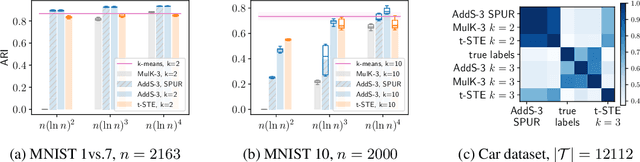
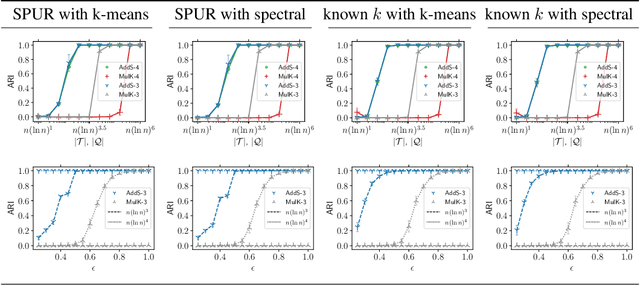
The goal of clustering is to group similar objects into meaningful partitions. This process is well understood when an explicit similarity measure between the objects is given. However, far less is known when this information is not readily available and, instead, one only observes ordinal comparisons such as "object i is more similar to j than to k." In this paper, we tackle this problem using a two-step procedure: we estimate a pairwise similarity matrix from the comparisons before using a clustering method based on semi-definite programming (SDP). We theoretically show that our approach can exactly recover a planted clustering using a near-optimal number of passive comparisons. We empirically validate our theoretical findings and demonstrate the good behaviour of our method on real data.

Foundations of Comparison-Based Hierarchical Clustering

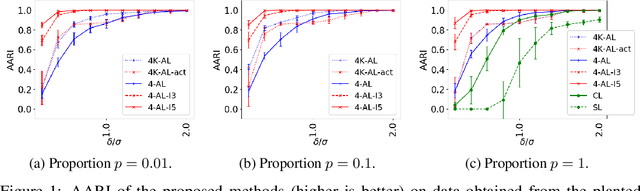
We address the classical problem of hierarchical clustering, but in a framework where one does not have access to a representation of the objects or their pairwise similarities. Instead we assume that only a set of comparisons between objects are available in terms of statements of the form "objects $i$ and $j$ are more similar than objects $k$ and $l$". Such a scenario is commonly encountered in crowdsourcing applications. The focus of this work is to develop comparison-based hierarchical clustering algorithms that do not rely on the principles of ordinal embedding. We propose comparison-based variants of average linkage clustering. We provide statistical guarantees for the proposed methods under a planted partition model for hierarchical clustering. We also empirically demonstrate the performance of the proposed methods on several datasets.

Boosting for Comparison-Based Learning

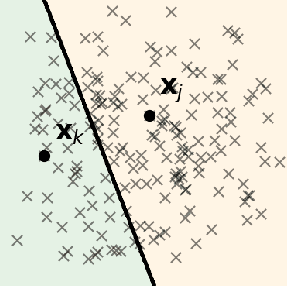
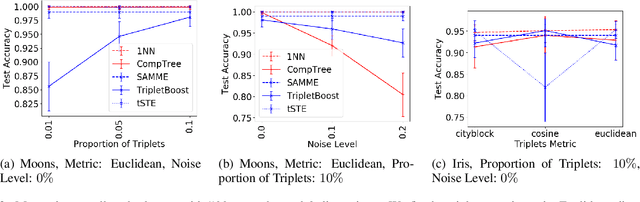
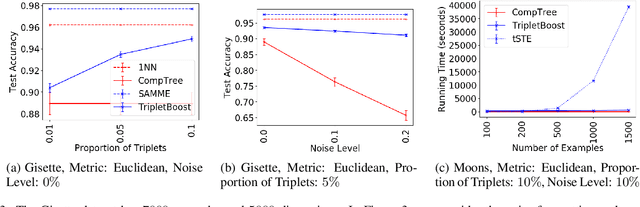
We consider the problem of classification in a comparison-based setting: given a set of objects, we only have access to triplet comparisons of the form "object $x_i$ is closer to object $x_j$ than to object $x_k$.'' In this paper we introduce TripletBoost, a new method that can learn a classifier just from such triplet comparisons. The main idea is to aggregate the triplets information into weak classifiers, which can subsequently be boosted to a strong classifier. Our method has two main advantages: (i) it is applicable to data from any metric space, and (ii) it can deal with large scale problems using only passively obtained and noisy triplets. We derive theoretical generalization guarantees and a lower bound on the number of necessary triplets, and we empirically show that our method is both competitive with state of the art approaches and resistant to noise.