Aurélien Bellet
PREMEDICAL, UM
Federated Learning for MRI-based BrainAGE: a multicenter study on post-stroke functional outcome prediction
Jun 18, 2025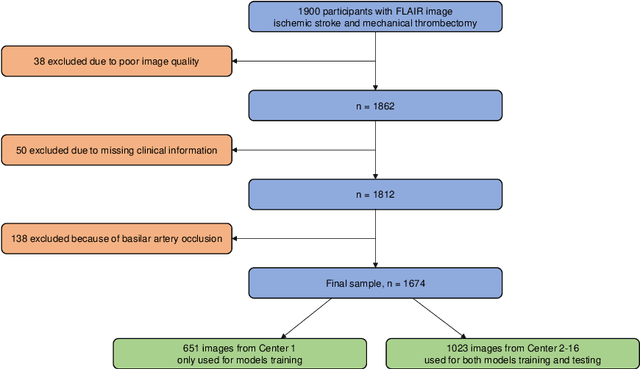
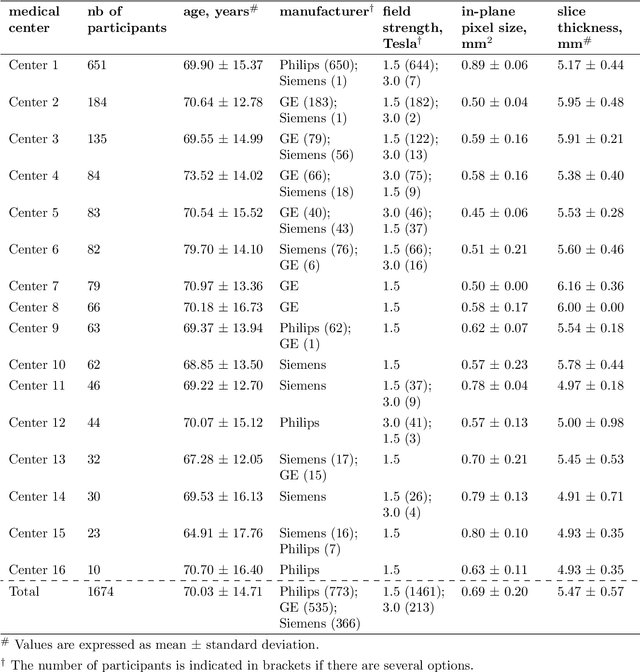
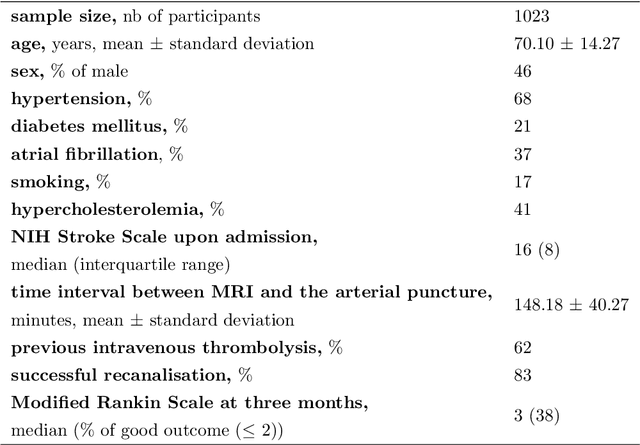
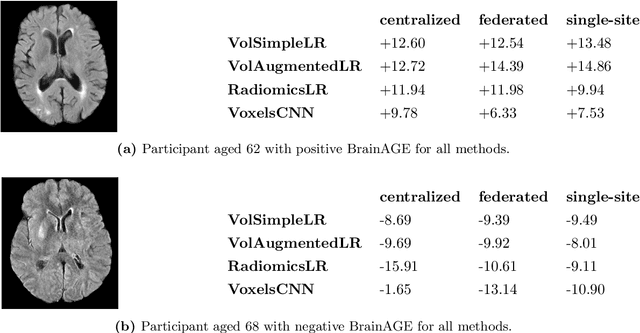
Abstract:$\textbf{Objective:}$ Brain-predicted age difference (BrainAGE) is a neuroimaging biomarker reflecting brain health. However, training robust BrainAGE models requires large datasets, often restricted by privacy concerns. This study evaluates the performance of federated learning (FL) for BrainAGE estimation in ischemic stroke patients treated with mechanical thrombectomy, and investigates its association with clinical phenotypes and functional outcomes. $\textbf{Methods:}$ We used FLAIR brain images from 1674 stroke patients across 16 hospital centers. We implemented standard machine learning and deep learning models for BrainAGE estimates under three data management strategies: centralized learning (pooled data), FL (local training at each site), and single-site learning. We reported prediction errors and examined associations between BrainAGE and vascular risk factors (e.g., diabetes mellitus, hypertension, smoking), as well as functional outcomes at three months post-stroke. Logistic regression evaluated BrainAGE's predictive value for these outcomes, adjusting for age, sex, vascular risk factors, stroke severity, time between MRI and arterial puncture, prior intravenous thrombolysis, and recanalisation outcome. $\textbf{Results:}$ While centralized learning yielded the most accurate predictions, FL consistently outperformed single-site models. BrainAGE was significantly higher in patients with diabetes mellitus across all models. Comparisons between patients with good and poor functional outcomes, and multivariate predictions of these outcomes showed the significance of the association between BrainAGE and post-stroke recovery. $\textbf{Conclusion:}$ FL enables accurate age predictions without data centralization. The strong association between BrainAGE, vascular risk factors, and post-stroke recovery highlights its potential for prognostic modeling in stroke care.
Privacy Amplification Through Synthetic Data: Insights from Linear Regression
Jun 05, 2025Abstract:Synthetic data inherits the differential privacy guarantees of the model used to generate it. Additionally, synthetic data may benefit from privacy amplification when the generative model is kept hidden. While empirical studies suggest this phenomenon, a rigorous theoretical understanding is still lacking. In this paper, we investigate this question through the well-understood framework of linear regression. First, we establish negative results showing that if an adversary controls the seed of the generative model, a single synthetic data point can leak as much information as releasing the model itself. Conversely, we show that when synthetic data is generated from random inputs, releasing a limited number of synthetic data points amplifies privacy beyond the model's inherent guarantees. We believe our findings in linear regression can serve as a foundation for deriving more general bounds in the future.
Private Rate-Constrained Optimization with Applications to Fair Learning
May 28, 2025Abstract:Many problems in trustworthy ML can be formulated as minimization of the model error under constraints on the prediction rates of the model for suitably-chosen marginals, including most group fairness constraints (demographic parity, equality of odds, etc.). In this work, we study such constrained minimization problems under differential privacy (DP). Standard DP optimization techniques like DP-SGD rely on the loss function's decomposability into per-sample contributions. However, rate constraints introduce inter-sample dependencies, violating the decomposability requirement. To address this, we develop RaCO-DP, a DP variant of the Stochastic Gradient Descent-Ascent (SGDA) algorithm which solves the Lagrangian formulation of rate constraint problems. We demonstrate that the additional privacy cost of incorporating these constraints reduces to privately estimating a histogram over the mini-batch at each optimization step. We prove the convergence of our algorithm through a novel analysis of SGDA that leverages the linear structure of the dual parameter. Finally, empirical results on learning under group fairness constraints demonstrate that our method Pareto-dominates existing private learning approaches in fairness-utility trade-offs.
Model Agnostic Differentially Private Causal Inference
May 26, 2025Abstract:Estimating causal effects from observational data is essential in fields such as medicine, economics and social sciences, where privacy concerns are paramount. We propose a general, model-agnostic framework for differentially private estimation of average treatment effects (ATE) that avoids strong structural assumptions on the data-generating process or the models used to estimate propensity scores and conditional outcomes. In contrast to prior work, which enforces differential privacy by directly privatizing these nuisance components and results in a privacy cost that scales with model complexity, our approach decouples nuisance estimation from privacy protection. This separation allows the use of flexible, state-of-the-art black-box models, while differential privacy is achieved by perturbing only predictions and aggregation steps within a fold-splitting scheme with ensemble techniques. We instantiate the framework for three classical estimators -- the G-formula, inverse propensity weighting (IPW), and augmented IPW (AIPW) -- and provide formal utility and privacy guarantees. Empirical results show that our methods maintain competitive performance under realistic privacy budgets. We further extend our framework to support meta-analysis of multiple private ATE estimates. Our results bridge a critical gap between causal inference and privacy-preserving data analysis.
Optimal Transport with Heterogeneously Missing Data
May 22, 2025Abstract:We consider the problem of solving the optimal transport problem between two empirical distributions with missing values. Our main assumption is that the data is missing completely at random (MCAR), but we allow for heterogeneous missingness probabilities across features and across the two distributions. As a first contribution, we show that the Wasserstein distance between empirical Gaussian distributions and linear Monge maps between arbitrary distributions can be debiased without significantly affecting the sample complexity. Secondly, we show that entropic regularized optimal transport can be estimated efficiently and consistently using iterative singular value thresholding (ISVT). We propose a validation set-free hyperparameter selection strategy for ISVT that leverages our estimator of the Bures-Wasserstein distance, which could be of independent interest in general matrix completion problems. Finally, we validate our findings on a wide range of numerical applications.
Federated Causal Inference: Multi-Centric ATE Estimation beyond Meta-Analysis
Oct 22, 2024Abstract:We study Federated Causal Inference, an approach to estimate treatment effects from decentralized data across centers. We compare three classes of Average Treatment Effect (ATE) estimators derived from the Plug-in G-Formula, ranging from simple meta-analysis to one-shot and multi-shot federated learning, the latter leveraging the full data to learn the outcome model (albeit requiring more communication). Focusing on Randomized Controlled Trials (RCTs), we derive the asymptotic variance of these estimators for linear models. Our results provide practical guidance on selecting the appropriate estimator for various scenarios, including heterogeneity in sample sizes, covariate distributions, treatment assignment schemes, and center effects. We validate these findings with a simulation study.
Tighter Privacy Auditing of DP-SGD in the Hidden State Threat Model
May 23, 2024Abstract:Machine learning models can be trained with formal privacy guarantees via differentially private optimizers such as DP-SGD. In this work, we study such privacy guarantees when the adversary only accesses the final model, i.e., intermediate model updates are not released. In the existing literature, this hidden state threat model exhibits a significant gap between the lower bound provided by empirical privacy auditing and the theoretical upper bound provided by privacy accounting. To challenge this gap, we propose to audit this threat model with adversaries that craft a gradient sequence to maximize the privacy loss of the final model without accessing intermediate models. We demonstrate experimentally how this approach consistently outperforms prior attempts at auditing the hidden state model. When the crafted gradient is inserted at every optimization step, our results imply that releasing only the final model does not amplify privacy, providing a novel negative result. On the other hand, when the crafted gradient is not inserted at every step, we show strong evidence that a privacy amplification phenomenon emerges in the general non-convex setting (albeit weaker than in convex regimes), suggesting that existing privacy upper bounds can be improved.
Synthetic Data Generation for Intersectional Fairness by Leveraging Hierarchical Group Structure
May 23, 2024Abstract:In this paper, we introduce a data augmentation approach specifically tailored to enhance intersectional fairness in classification tasks. Our method capitalizes on the hierarchical structure inherent to intersectionality, by viewing groups as intersections of their parent categories. This perspective allows us to augment data for smaller groups by learning a transformation function that combines data from these parent groups. Our empirical analysis, conducted on four diverse datasets including both text and images, reveals that classifiers trained with this data augmentation approach achieve superior intersectional fairness and are more robust to ``leveling down'' when compared to methods optimizing traditional group fairness metrics.
Marginal and training-conditional guarantees in one-shot federated conformal prediction
May 21, 2024Abstract:We study conformal prediction in the one-shot federated learning setting. The main goal is to compute marginally and training-conditionally valid prediction sets, at the server-level, in only one round of communication between the agents and the server. Using the quantile-of-quantiles family of estimators and split conformal prediction, we introduce a collection of computationally-efficient and distribution-free algorithms that satisfy the aforementioned requirements. Our approaches come from theoretical results related to order statistics and the analysis of the Beta-Beta distribution. We also prove upper bounds on the coverage of all proposed algorithms when the nonconformity scores are almost surely distinct. For algorithms with training-conditional guarantees, these bounds are of the same order of magnitude as those of the centralized case. Remarkably, this implies that the one-shot federated learning setting entails no significant loss compared to the centralized case. Our experiments confirm that our algorithms return prediction sets with coverage and length similar to those obtained in a centralized setting.
Privacy Attacks in Decentralized Learning
Feb 15, 2024Abstract:Decentralized Gradient Descent (D-GD) allows a set of users to perform collaborative learning without sharing their data by iteratively averaging local model updates with their neighbors in a network graph. The absence of direct communication between non-neighbor nodes might lead to the belief that users cannot infer precise information about the data of others. In this work, we demonstrate the opposite, by proposing the first attack against D-GD that enables a user (or set of users) to reconstruct the private data of other users outside their immediate neighborhood. Our approach is based on a reconstruction attack against the gossip averaging protocol, which we then extend to handle the additional challenges raised by D-GD. We validate the effectiveness of our attack on real graphs and datasets, showing that the number of users compromised by a single or a handful of attackers is often surprisingly large. We empirically investigate some of the factors that affect the performance of the attack, namely the graph topology, the number of attackers, and their position in the graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge