Privacy Amplification Through Synthetic Data: Insights from Linear Regression

Synthetic data inherits the differential privacy guarantees of the model used to generate it. Additionally, synthetic data may benefit from privacy amplification when the generative model is kept hidden. While empirical studies suggest this phenomenon, a rigorous theoretical understanding is still lacking. In this paper, we investigate this question through the well-understood framework of linear regression. First, we establish negative results showing that if an adversary controls the seed of the generative model, a single synthetic data point can leak as much information as releasing the model itself. Conversely, we show that when synthetic data is generated from random inputs, releasing a limited number of synthetic data points amplifies privacy beyond the model's inherent guarantees. We believe our findings in linear regression can serve as a foundation for deriving more general bounds in the future.

The Impact of LoRA on the Emergence of Clusters in Transformers

In this paper, we employ the mathematical framework on Transformers developed by \citet{sander2022sinkformers,geshkovski2023emergence,geshkovski2023mathematical} to explore how variations in attention parameters and initial token values impact the structural dynamics of token clusters. Our analysis demonstrates that while the clusters within a modified attention matrix dynamics can exhibit significant divergence from the original over extended periods, they maintain close similarities over shorter intervals, depending on the parameter differences. This work contributes to the fine-tuning field through practical applications to the LoRA algorithm \cite{hu2021lora,peft}, enhancing our understanding of the behavior of LoRA-enhanced Transformer models.

Rényi Pufferfish Privacy: General Additive Noise Mechanisms and Privacy Amplification by Iteration

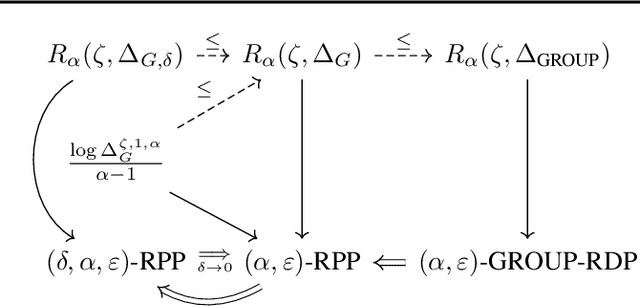
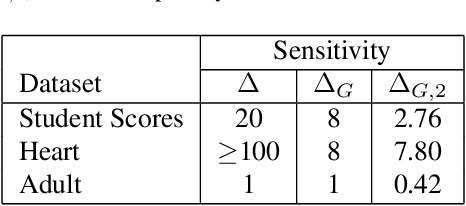
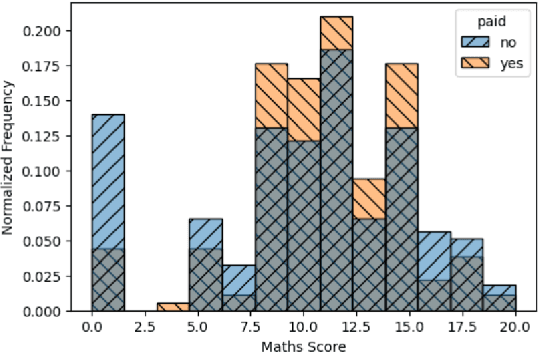
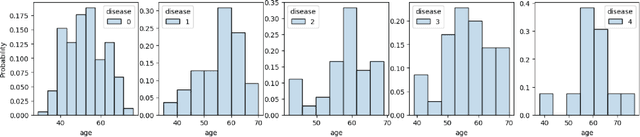
Pufferfish privacy is a flexible generalization of differential privacy that allows to model arbitrary secrets and adversary's prior knowledge about the data. Unfortunately, designing general and tractable Pufferfish mechanisms that do not compromise utility is challenging. Furthermore, this framework does not provide the composition guarantees needed for a direct use in iterative machine learning algorithms. To mitigate these issues, we introduce a R\'enyi divergence-based variant of Pufferfish and show that it allows us to extend the applicability of the Pufferfish framework. We first generalize the Wasserstein mechanism to cover a wide range of noise distributions and introduce several ways to improve its utility. We also derive stronger guarantees against out-of-distribution adversaries. Finally, as an alternative to composition, we prove privacy amplification results for contractive noisy iterations and showcase the first use of Pufferfish in private convex optimization. A common ingredient underlying our results is the use and extension of shift reduction lemmas.

Information gain ratio correction: Improving prediction with more balanced decision tree splits

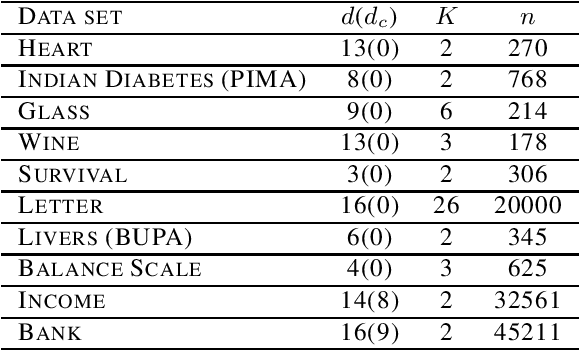
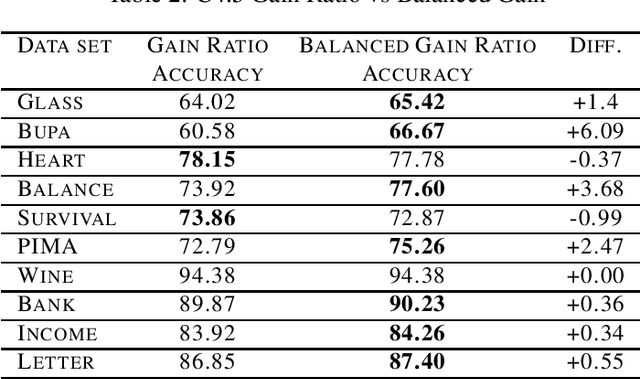
Decision trees algorithms use a gain function to select the best split during the tree's induction. This function is crucial to obtain trees with high predictive accuracy. Some gain functions can suffer from a bias when it compares splits of different arities. Quinlan proposed a gain ratio in C4.5's information gain function to fix this bias. In this paper, we present an updated version of the gain ratio that performs better as it tries to fix the gain ratio's bias for unbalanced trees and some splits with low predictive interest.