Privacy Amplification Persists under Unlimited Synthetic Data Release

We study privacy amplification by synthetic data release, a phenomenon in which differential privacy guarantees are improved by releasing only synthetic data rather than the private generative model itself. Recent work by Pierquin et al. (2025) established the first formal amplification guarantees for a linear generator, but they apply only in asymptotic regimes where the model dimension far exceeds the number of released synthetic records, limiting their practical relevance. In this work, we show a surprising result: under a bounded-parameter assumption, privacy amplification persists even when releasing an unbounded number of synthetic records, thereby improving upon the bounds of Pierquin et al. (2025). Our analysis provides structural insights that may guide the development of tighter privacy guarantees for more complex release mechanisms.

Privacy Amplification Through Synthetic Data: Insights from Linear Regression

Synthetic data inherits the differential privacy guarantees of the model used to generate it. Additionally, synthetic data may benefit from privacy amplification when the generative model is kept hidden. While empirical studies suggest this phenomenon, a rigorous theoretical understanding is still lacking. In this paper, we investigate this question through the well-understood framework of linear regression. First, we establish negative results showing that if an adversary controls the seed of the generative model, a single synthetic data point can leak as much information as releasing the model itself. Conversely, we show that when synthetic data is generated from random inputs, releasing a limited number of synthetic data points amplifies privacy beyond the model's inherent guarantees. We believe our findings in linear regression can serve as a foundation for deriving more general bounds in the future.

Rényi Pufferfish Privacy: General Additive Noise Mechanisms and Privacy Amplification by Iteration

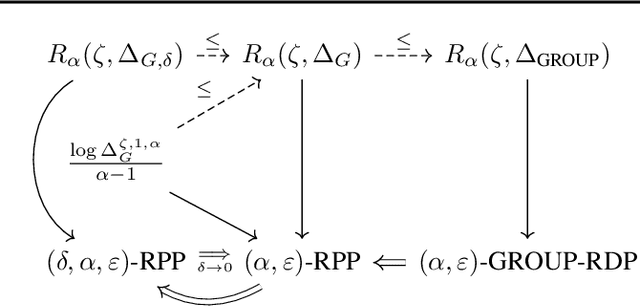
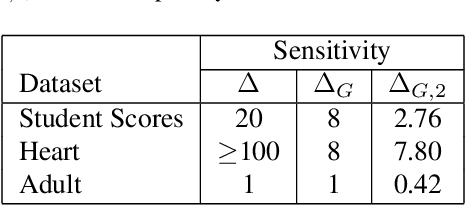
Pufferfish privacy is a flexible generalization of differential privacy that allows to model arbitrary secrets and adversary's prior knowledge about the data. Unfortunately, designing general and tractable Pufferfish mechanisms that do not compromise utility is challenging. Furthermore, this framework does not provide the composition guarantees needed for a direct use in iterative machine learning algorithms. To mitigate these issues, we introduce a R\'enyi divergence-based variant of Pufferfish and show that it allows us to extend the applicability of the Pufferfish framework. We first generalize the Wasserstein mechanism to cover a wide range of noise distributions and introduce several ways to improve its utility. We also derive stronger guarantees against out-of-distribution adversaries. Finally, as an alternative to composition, we prove privacy amplification results for contractive noisy iterations and showcase the first use of Pufferfish in private convex optimization. A common ingredient underlying our results is the use and extension of shift reduction lemmas.