Rényi Pufferfish Privacy: General Additive Noise Mechanisms and Privacy Amplification by Iteration

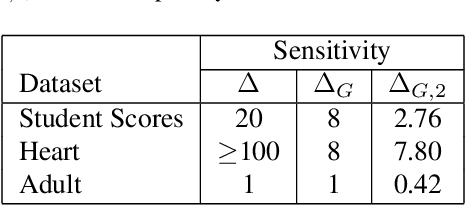
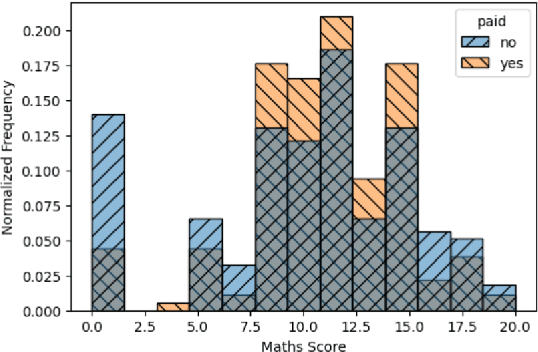
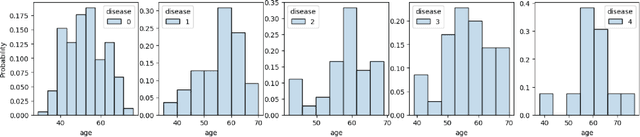
Pufferfish privacy is a flexible generalization of differential privacy that allows to model arbitrary secrets and adversary's prior knowledge about the data. Unfortunately, designing general and tractable Pufferfish mechanisms that do not compromise utility is challenging. Furthermore, this framework does not provide the composition guarantees needed for a direct use in iterative machine learning algorithms. To mitigate these issues, we introduce a R\'enyi divergence-based variant of Pufferfish and show that it allows us to extend the applicability of the Pufferfish framework. We first generalize the Wasserstein mechanism to cover a wide range of noise distributions and introduce several ways to improve its utility. We also derive stronger guarantees against out-of-distribution adversaries. Finally, as an alternative to composition, we prove privacy amplification results for contractive noisy iterations and showcase the first use of Pufferfish in private convex optimization. A common ingredient underlying our results is the use and extension of shift reduction lemmas.