Optimal Transport with Heterogeneously Missing Data

We consider the problem of solving the optimal transport problem between two empirical distributions with missing values. Our main assumption is that the data is missing completely at random (MCAR), but we allow for heterogeneous missingness probabilities across features and across the two distributions. As a first contribution, we show that the Wasserstein distance between empirical Gaussian distributions and linear Monge maps between arbitrary distributions can be debiased without significantly affecting the sample complexity. Secondly, we show that entropic regularized optimal transport can be estimated efficiently and consistently using iterative singular value thresholding (ISVT). We propose a validation set-free hyperparameter selection strategy for ISVT that leverages our estimator of the Bures-Wasserstein distance, which could be of independent interest in general matrix completion problems. Finally, we validate our findings on a wide range of numerical applications.

Predicting gene essentiality and drug response from perturbation screens in preclinical cancer models with LEAP: Layered Ensemble of Autoencoders and Predictors

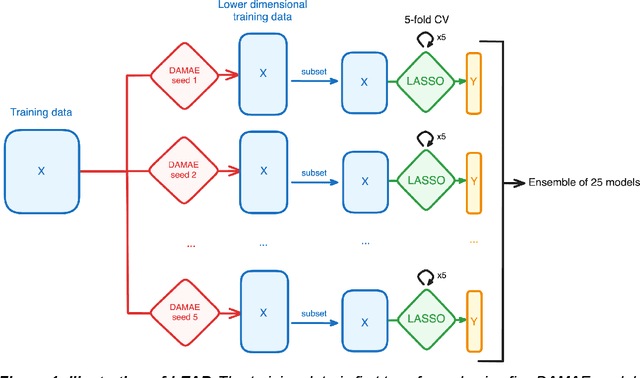
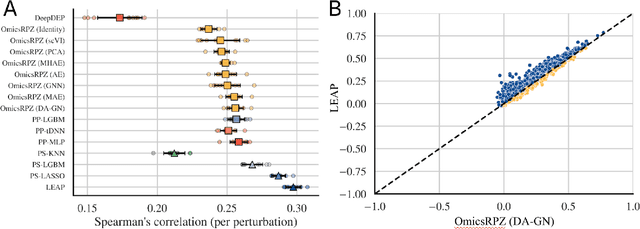
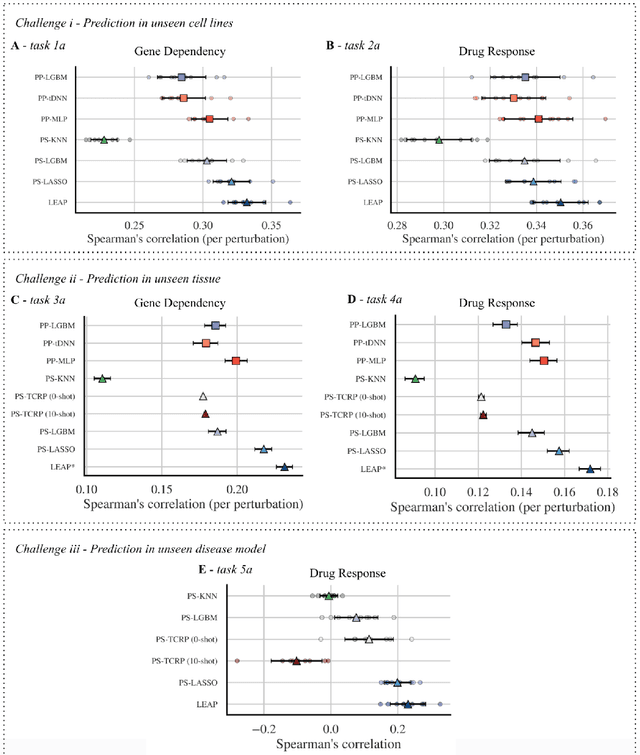
Preclinical perturbation screens, where the effects of genetic, chemical, or environmental perturbations are systematically tested on disease models, hold significant promise for machine learning-enhanced drug discovery due to their scale and causal nature. Predictive models can infer perturbation responses for previously untested disease models based on molecular profiles. These in silico labels can expand databases and guide experimental prioritization. However, modelling perturbation-specific effects and generating robust prediction performances across diverse biological contexts remain elusive. We introduce LEAP (Layered Ensemble of Autoencoders and Predictors), a novel ensemble framework to improve robustness and generalization. LEAP leverages multiple DAMAE (Data Augmented Masked Autoencoder) representations and LASSO regressors. By combining diverse gene expression representation models learned from different random initializations, LEAP consistently outperforms state-of-the-art approaches in predicting gene essentiality or drug responses in unseen cell lines, tissues and disease models. Notably, our results show that ensembling representation models, rather than prediction models alone, yields superior predictive performance. Beyond its performance gains, LEAP is computationally efficient, requires minimal hyperparameter tuning and can therefore be readily incorporated into drug discovery pipelines to prioritize promising targets and support biomarker-driven stratification. The code and datasets used in this work are made publicly available.

Large Language Models as Markov Chains

Large language models (LLMs) have proven to be remarkably efficient, both across a wide range of natural language processing tasks and well beyond them. However, a comprehensive theoretical analysis of the origins of their impressive performance remains elusive. In this paper, we approach this challenging task by drawing an equivalence between generic autoregressive language models with vocabulary of size $T$ and context window of size $K$ and Markov chains defined on a finite state space of size $\mathcal{O}(T^K)$. We derive several surprising findings related to the existence of a stationary distribution of Markov chains that capture the inference power of LLMs, their speed of convergence to it, and the influence of the temperature on the latter. We then prove pre-training and in-context generalization bounds and show how the drawn equivalence allows us to enrich their interpretation. Finally, we illustrate our theoretical guarantees with experiments on several recent LLMs to highlight how they capture the behavior observed in practice.

Dynamical Survival Analysis with Controlled Latent States

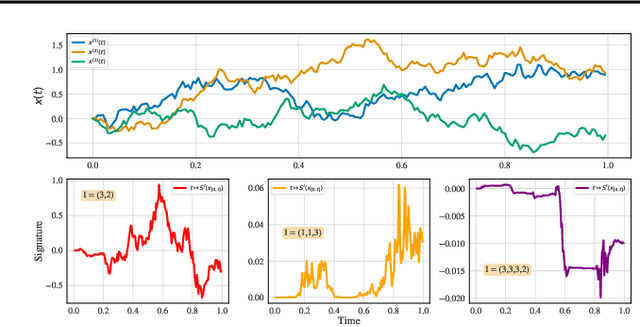
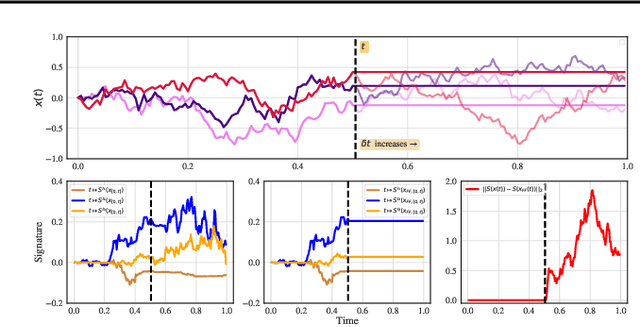
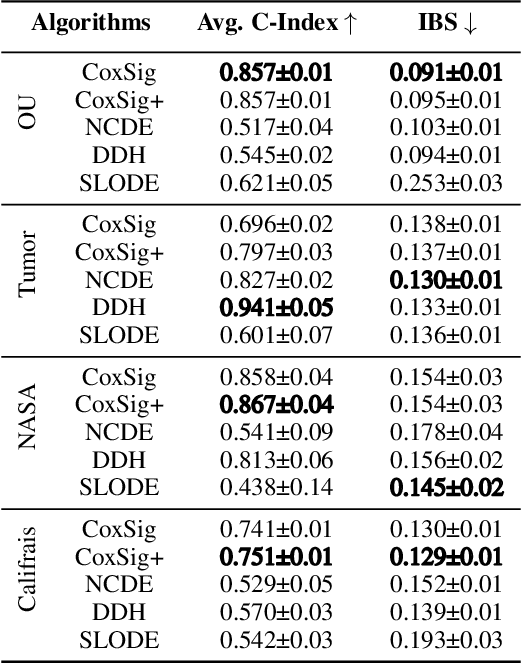
We consider the task of learning individual-specific intensities of counting processes from a set of static variables and irregularly sampled time series. We introduce a novel modelization approach in which the intensity is the solution to a controlled differential equation. We first design a neural estimator by building on neural controlled differential equations. In a second time, we show that our model can be linearized in the signature space under sufficient regularity conditions, yielding a signature-based estimator which we call CoxSig. We provide theoretical learning guarantees for both estimators, before showcasing the performance of our models on a vast array of simulated and real-world datasets from finance, predictive maintenance and food supply chain management.

On the Generalization Capacities of Neural Controlled Differential Equations

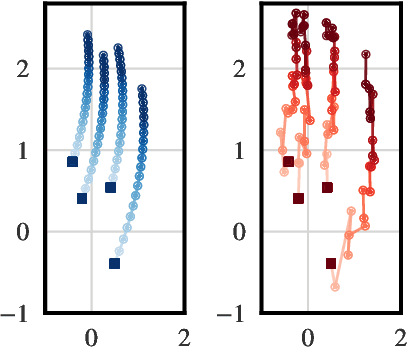
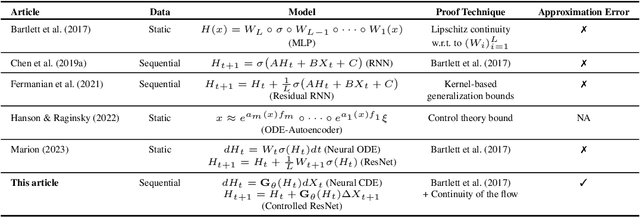
We consider a supervised learning setup in which the goal is to predicts an outcome from a sample of irregularly sampled time series using Neural Controlled Differential Equations (Kidger, Morrill, et al. 2020). In our framework, the time series is a discretization of an unobserved continuous path, and the outcome depends on this path through a controlled differential equation with unknown vector field. Learning with discrete data thus induces a discretization bias, which we precisely quantify. Using theoretical results on the continuity of the flow of controlled differential equations, we show that the approximation bias is directly related to the approximation error of a Lipschitz function defining the generative model by a shallow neural network. By combining these result with recent work linking the Lipschitz constant of neural networks to their generalization capacities, we upper bound the generalization gap between the expected loss attained by the empirical risk minimizer and the expected loss of the true predictor.

Learning the Dynamics of Sparsely Observed Interacting Systems

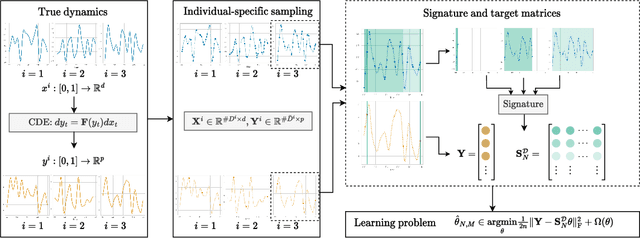
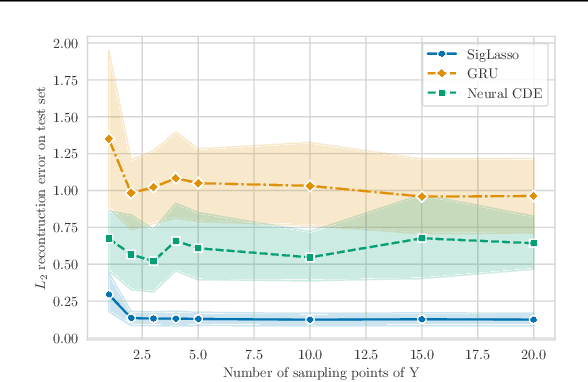
We address the problem of learning the dynamics of an unknown non-parametric system linking a target and a feature time series. The feature time series is measured on a sparse and irregular grid, while we have access to only a few points of the target time series. Once learned, we can use these dynamics to predict values of the target from the previous values of the feature time series. We frame this task as learning the solution map of a controlled differential equation (CDE). By leveraging the rich theory of signatures, we are able to cast this non-linear problem as a high-dimensional linear regression. We provide an oracle bound on the prediction error which exhibits explicit dependencies on the individual-specific sampling schemes. Our theoretical results are illustrated by simulations which show that our method outperforms existing algorithms for recovering the full time series while being computationally cheap. We conclude by demonstrating its potential on real-world epidemiological data.