TAG: A Decentralized Framework for Multi-Agent Hierarchical Reinforcement Learning

Hierarchical organization is fundamental to biological systems and human societies, yet artificial intelligence systems often rely on monolithic architectures that limit adaptability and scalability. Current hierarchical reinforcement learning (HRL) approaches typically restrict hierarchies to two levels or require centralized training, which limits their practical applicability. We introduce TAME Agent Framework (TAG), a framework for constructing fully decentralized hierarchical multi-agent systems.TAG enables hierarchies of arbitrary depth through a novel LevelEnv concept, which abstracts each hierarchy level as the environment for the agents above it. This approach standardizes information flow between levels while preserving loose coupling, allowing for seamless integration of diverse agent types. We demonstrate the effectiveness of TAG by implementing hierarchical architectures that combine different RL agents across multiple levels, achieving improved performance over classical multi-agent RL baselines on standard benchmarks. Our results show that decentralized hierarchical organization enhances both learning speed and final performance, positioning TAG as a promising direction for scalable multi-agent systems.

Large Language Models Orchestrating Structured Reasoning Achieve Kaggle Grandmaster Level

We introduce Agent K v1.0, an end-to-end autonomous data science agent designed to automate, optimise, and generalise across diverse data science tasks. Fully automated, Agent K v1.0 manages the entire data science life cycle by learning from experience. It leverages a highly flexible structured reasoning framework to enable it to dynamically process memory in a nested structure, effectively learning from accumulated experience stored to handle complex reasoning tasks. It optimises long- and short-term memory by selectively storing and retrieving key information, guiding future decisions based on environmental rewards. This iterative approach allows it to refine decisions without fine-tuning or backpropagation, achieving continuous improvement through experiential learning. We evaluate our agent's apabilities using Kaggle competitions as a case study. Following a fully automated protocol, Agent K v1.0 systematically addresses complex and multimodal data science tasks, employing Bayesian optimisation for hyperparameter tuning and feature engineering. Our new evaluation framework rigorously assesses Agent K v1.0's end-to-end capabilities to generate and send submissions starting from a Kaggle competition URL. Results demonstrate that Agent K v1.0 achieves a 92.5\% success rate across tasks, spanning tabular, computer vision, NLP, and multimodal domains. When benchmarking against 5,856 human Kaggle competitors by calculating Elo-MMR scores for each, Agent K v1.0 ranks in the top 38\%, demonstrating an overall skill level comparable to Expert-level users. Notably, its Elo-MMR score falls between the first and third quartiles of scores achieved by human Grandmasters. Furthermore, our results indicate that Agent K v1.0 has reached a performance level equivalent to Kaggle Grandmaster, with a record of 6 gold, 3 silver, and 7 bronze medals, as defined by Kaggle's progression system.

Zero-shot Model-based Reinforcement Learning using Large Language Models

The emerging zero-shot capabilities of Large Language Models (LLMs) have led to their applications in areas extending well beyond natural language processing tasks. In reinforcement learning, while LLMs have been extensively used in text-based environments, their integration with continuous state spaces remains understudied. In this paper, we investigate how pre-trained LLMs can be leveraged to predict in context the dynamics of continuous Markov decision processes. We identify handling multivariate data and incorporating the control signal as key challenges that limit the potential of LLMs' deployment in this setup and propose Disentangled In-Context Learning (DICL) to address them. We present proof-of-concept applications in two reinforcement learning settings: model-based policy evaluation and data-augmented off-policy reinforcement learning, supported by theoretical analysis of the proposed methods. Our experiments further demonstrate that our approach produces well-calibrated uncertainty estimates. We release the code at https://github.com/abenechehab/dicl.

Large Language Models as Markov Chains

Large language models (LLMs) have proven to be remarkably efficient, both across a wide range of natural language processing tasks and well beyond them. However, a comprehensive theoretical analysis of the origins of their impressive performance remains elusive. In this paper, we approach this challenging task by drawing an equivalence between generic autoregressive language models with vocabulary of size $T$ and context window of size $K$ and Markov chains defined on a finite state space of size $\mathcal{O}(T^K)$. We derive several surprising findings related to the existence of a stationary distribution of Markov chains that capture the inference power of LLMs, their speed of convergence to it, and the influence of the temperature on the latter. We then prove pre-training and in-context generalization bounds and show how the drawn equivalence allows us to enrich their interpretation. Finally, we illustrate our theoretical guarantees with experiments on several recent LLMs to highlight how they capture the behavior observed in practice.

Can LLMs predict the convergence of Stochastic Gradient Descent?

Large-language models are notoriously famous for their impressive performance across a wide range of tasks. One surprising example of such impressive performance is a recently identified capacity of LLMs to understand the governing principles of dynamical systems satisfying the Markovian property. In this paper, we seek to explore this direction further by studying the dynamics of stochastic gradient descent in convex and non-convex optimization. By leveraging the theoretical link between the SGD and Markov chains, we show a remarkable zero-shot performance of LLMs in predicting the local minima to which SGD converges for previously unseen starting points. On a more general level, we inquire about the possibility of using LLMs to perform zero-shot randomized trials for larger deep learning models used in practice.

A Multi-step Loss Function for Robust Learning of the Dynamics in Model-based Reinforcement Learning

In model-based reinforcement learning, most algorithms rely on simulating trajectories from one-step models of the dynamics learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as the length of the trajectory grows. In this paper we tackle this issue by using a multi-step objective to train one-step models. Our objective is a weighted sum of the mean squared error (MSE) loss at various future horizons. We find that this new loss is particularly useful when the data is noisy (additive Gaussian noise in the observations), which is often the case in real-life environments. To support the multi-step loss, first we study its properties in two tractable cases: i) uni-dimensional linear system, and ii) two-parameter non-linear system. Second, we show in a variety of tasks (environments or datasets) that the models learned with this loss achieve a significant improvement in terms of the averaged R2-score on future prediction horizons. Finally, in the pure batch reinforcement learning setting, we demonstrate that one-step models serve as strong baselines when dynamics are deterministic, while multi-step models would be more advantageous in the presence of noise, highlighting the potential of our approach in real-world applications.

Deep autoregressive density nets vs neural ensembles for model-based offline reinforcement learning

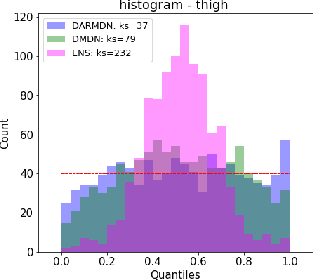
We consider the problem of offline reinforcement learning where only a set of system transitions is made available for policy optimization. Following recent advances in the field, we consider a model-based reinforcement learning algorithm that infers the system dynamics from the available data and performs policy optimization on imaginary model rollouts. This approach is vulnerable to exploiting model errors which can lead to catastrophic failures on the real system. The standard solution is to rely on ensembles for uncertainty heuristics and to avoid exploiting the model where it is too uncertain. We challenge the popular belief that we must resort to ensembles by showing that better performance can be obtained with a single well-calibrated autoregressive model on the D4RL benchmark. We also analyze static metrics of model-learning and conclude on the important model properties for the final performance of the agent.

Multi-timestep models for Model-based Reinforcement Learning

In model-based reinforcement learning (MBRL), most algorithms rely on simulating trajectories from one-step dynamics models learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as length of the trajectory grows. In this paper we tackle this issue by using a multi-timestep objective to train one-step models. Our objective is a weighted sum of a loss function (e.g., negative log-likelihood) at various future horizons. We explore and test a range of weights profiles. We find that exponentially decaying weights lead to models that significantly improve the long-horizon R2 score. This improvement is particularly noticeable when the models were evaluated on noisy data. Finally, using a soft actor-critic (SAC) agent in pure batch reinforcement learning (RL) and iterated batch RL scenarios, we found that our multi-timestep models outperform or match standard one-step models. This was especially evident in a noisy variant of the considered environment, highlighting the potential of our approach in real-world applications.