Large Language Models Orchestrating Structured Reasoning Achieve Kaggle Grandmaster Level

We introduce Agent K v1.0, an end-to-end autonomous data science agent designed to automate, optimise, and generalise across diverse data science tasks. Fully automated, Agent K v1.0 manages the entire data science life cycle by learning from experience. It leverages a highly flexible structured reasoning framework to enable it to dynamically process memory in a nested structure, effectively learning from accumulated experience stored to handle complex reasoning tasks. It optimises long- and short-term memory by selectively storing and retrieving key information, guiding future decisions based on environmental rewards. This iterative approach allows it to refine decisions without fine-tuning or backpropagation, achieving continuous improvement through experiential learning. We evaluate our agent's apabilities using Kaggle competitions as a case study. Following a fully automated protocol, Agent K v1.0 systematically addresses complex and multimodal data science tasks, employing Bayesian optimisation for hyperparameter tuning and feature engineering. Our new evaluation framework rigorously assesses Agent K v1.0's end-to-end capabilities to generate and send submissions starting from a Kaggle competition URL. Results demonstrate that Agent K v1.0 achieves a 92.5\% success rate across tasks, spanning tabular, computer vision, NLP, and multimodal domains. When benchmarking against 5,856 human Kaggle competitors by calculating Elo-MMR scores for each, Agent K v1.0 ranks in the top 38\%, demonstrating an overall skill level comparable to Expert-level users. Notably, its Elo-MMR score falls between the first and third quartiles of scores achieved by human Grandmasters. Furthermore, our results indicate that Agent K v1.0 has reached a performance level equivalent to Kaggle Grandmaster, with a record of 6 gold, 3 silver, and 7 bronze medals, as defined by Kaggle's progression system.

End-to-End Meta-Bayesian Optimisation with Transformer Neural Processes

Meta-Bayesian optimisation (meta-BO) aims to improve the sample efficiency of Bayesian optimisation by leveraging data from related tasks. While previous methods successfully meta-learn either a surrogate model or an acquisition function independently, joint training of both components remains an open challenge. This paper proposes the first end-to-end differentiable meta-BO framework that generalises neural processes to learn acquisition functions via transformer architectures. We enable this end-to-end framework with reinforcement learning (RL) to tackle the lack of labelled acquisition data. Early on, we notice that training transformer-based neural processes from scratch with RL is challenging due to insufficient supervision, especially when rewards are sparse. We formalise this claim with a combinatorial analysis showing that the widely used notion of regret as a reward signal exhibits a logarithmic sparsity pattern in trajectory lengths. To tackle this problem, we augment the RL objective with an auxiliary task that guides part of the architecture to learn a valid probabilistic model as an inductive bias. We demonstrate that our method achieves state-of-the-art regret results against various baselines in experiments on standard hyperparameter optimisation tasks and also outperforms others in the real-world problems of mixed-integer programming tuning, antibody design, and logic synthesis for electronic design automation.

Sample-Efficient Optimisation with Probabilistic Transformer Surrogates

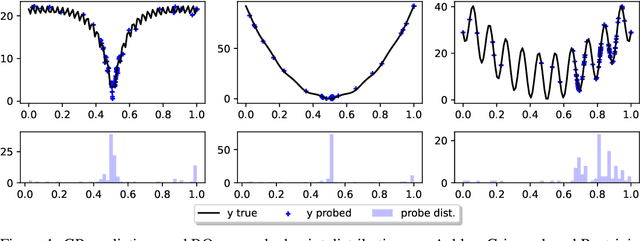
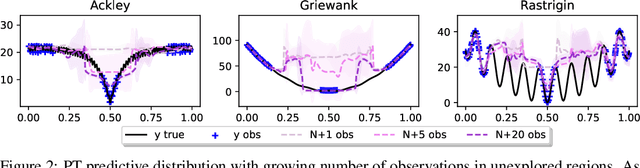
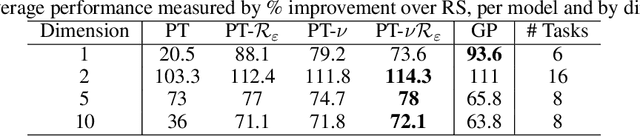
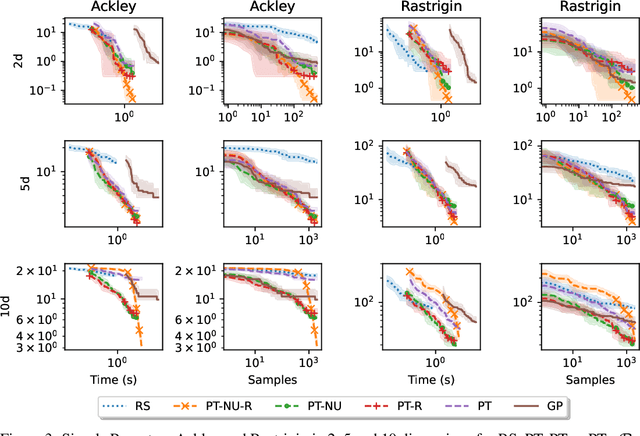
Faced with problems of increasing complexity, recent research in Bayesian Optimisation (BO) has focused on adapting deep probabilistic models as flexible alternatives to Gaussian Processes (GPs). In a similar vein, this paper investigates the feasibility of employing state-of-the-art probabilistic transformers in BO. Upon further investigation, we observe two drawbacks stemming from their training procedure and loss definition, hindering their direct deployment as proxies in black-box optimisation. First, we notice that these models are trained on uniformly distributed inputs, which impairs predictive accuracy on non-uniform data - a setting arising from any typical BO loop due to exploration-exploitation trade-offs. Second, we realise that training losses (e.g., cross-entropy) only asymptotically guarantee accurate posterior approximations, i.e., after arriving at the global optimum, which generally cannot be ensured. At the stationary points of the loss function, however, we observe a degradation in predictive performance especially in exploratory regions of the input space. To tackle these shortcomings we introduce two components: 1) a BO-tailored training prior supporting non-uniformly distributed points, and 2) a novel approximate posterior regulariser trading-off accuracy and input sensitivity to filter favourable stationary points for improved predictive performance. In a large panel of experiments, we demonstrate, for the first time, that one transformer pre-trained on data sampled from random GP priors produces competitive results on 16 benchmark black-boxes compared to GP-based BO. Since our model is only pre-trained once and used in all tasks without any retraining and/or fine-tuning, we report an order of magnitude time-reduction, while matching and sometimes outperforming GPs.

Efficient Semi-Implicit Variational Inference

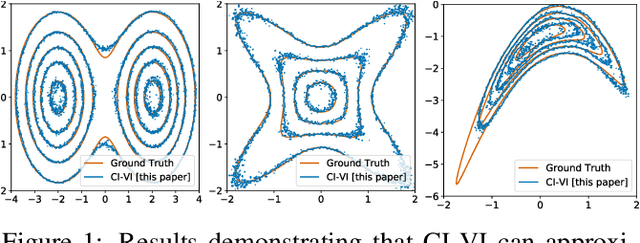
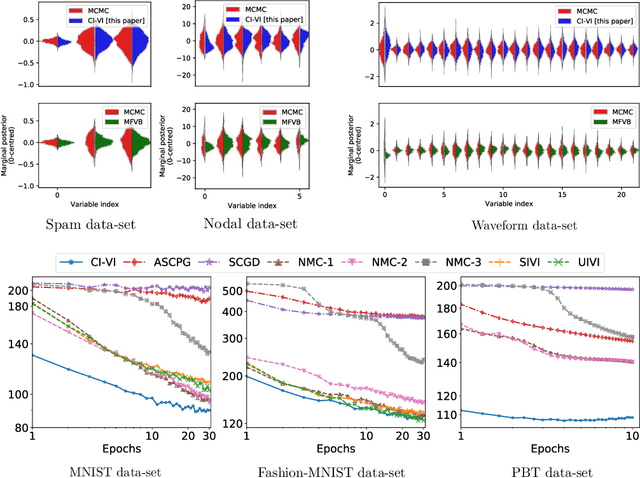
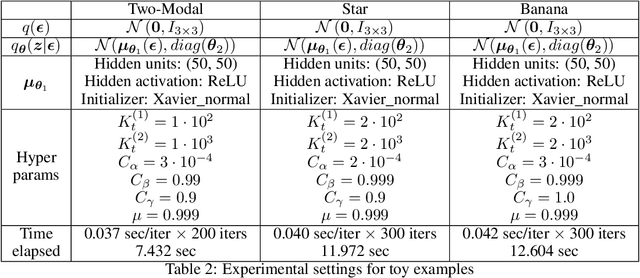
In this paper, we propose CI-VI an efficient and scalable solver for semi-implicit variational inference (SIVI). Our method, first, maps SIVI's evidence lower bound (ELBO) to a form involving a nonlinear functional nesting of expected values and then develops a rigorous optimiser capable of correctly handling bias inherent to nonlinear nested expectations using an extrapolation-smoothing mechanism coupled with gradient sketching. Our theoretical results demonstrate convergence to a stationary point of the ELBO in general non-convex settings typically arising when using deep network models and an order of $O(t^{-\frac{4}{5}})$ gradient-bias-vanishing rate. We believe these results generalise beyond the specific nesting arising from SIVI to other forms. Finally, in a set of experiments, we demonstrate the effectiveness of our algorithm in approximating complex posteriors on various data-sets including those from natural language processing.