Sample-Efficient Optimisation with Probabilistic Transformer Surrogates
Paper and Code
May 30, 2022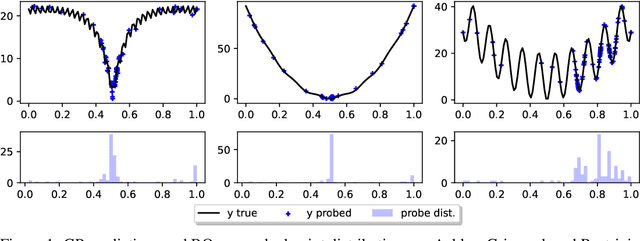
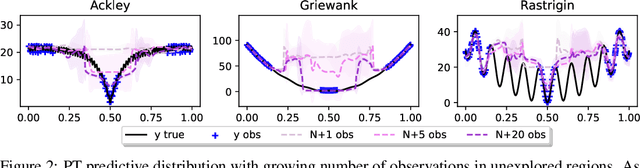
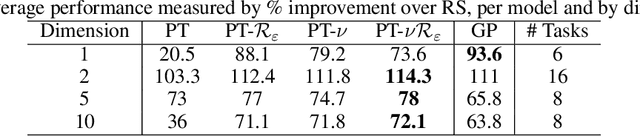
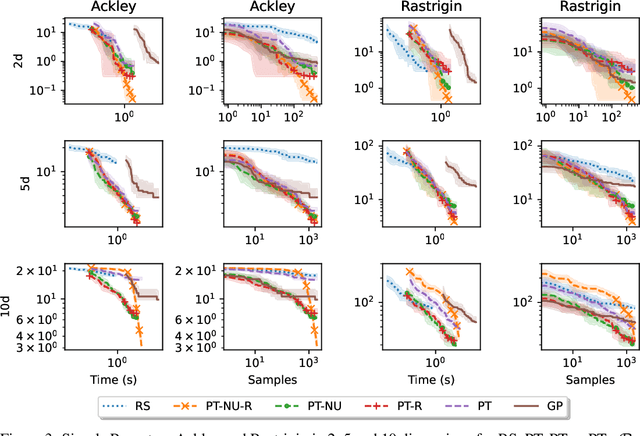
Faced with problems of increasing complexity, recent research in Bayesian Optimisation (BO) has focused on adapting deep probabilistic models as flexible alternatives to Gaussian Processes (GPs). In a similar vein, this paper investigates the feasibility of employing state-of-the-art probabilistic transformers in BO. Upon further investigation, we observe two drawbacks stemming from their training procedure and loss definition, hindering their direct deployment as proxies in black-box optimisation. First, we notice that these models are trained on uniformly distributed inputs, which impairs predictive accuracy on non-uniform data - a setting arising from any typical BO loop due to exploration-exploitation trade-offs. Second, we realise that training losses (e.g., cross-entropy) only asymptotically guarantee accurate posterior approximations, i.e., after arriving at the global optimum, which generally cannot be ensured. At the stationary points of the loss function, however, we observe a degradation in predictive performance especially in exploratory regions of the input space. To tackle these shortcomings we introduce two components: 1) a BO-tailored training prior supporting non-uniformly distributed points, and 2) a novel approximate posterior regulariser trading-off accuracy and input sensitivity to filter favourable stationary points for improved predictive performance. In a large panel of experiments, we demonstrate, for the first time, that one transformer pre-trained on data sampled from random GP priors produces competitive results on 16 benchmark black-boxes compared to GP-based BO. Since our model is only pre-trained once and used in all tasks without any retraining and/or fine-tuning, we report an order of magnitude time-reduction, while matching and sometimes outperforming GPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge