Why Can Large Language Models Generate Correct Chain-of-Thoughts?

This paper delves into the capabilities of large language models (LLMs), specifically focusing on advancing the theoretical comprehension of chain-of-thought prompting. We investigate how LLMs can be effectively induced to generate a coherent chain of thoughts. To achieve this, we introduce a two-level hierarchical graphical model tailored for natural language generation. Within this framework, we establish a compelling geometrical convergence rate that gauges the likelihood of an LLM-generated chain of thoughts compared to those originating from the true language. Our findings provide a theoretical justification for the ability of LLMs to produce the correct sequence of thoughts (potentially) explaining performance gains in tasks demanding reasoning skills.

Sample-Efficient Optimisation with Probabilistic Transformer Surrogates

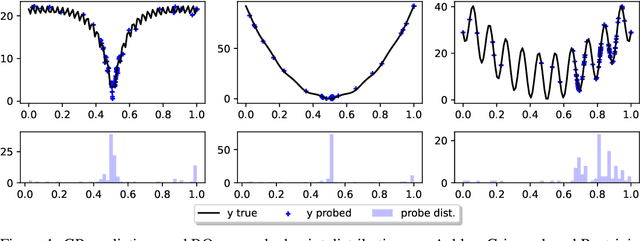
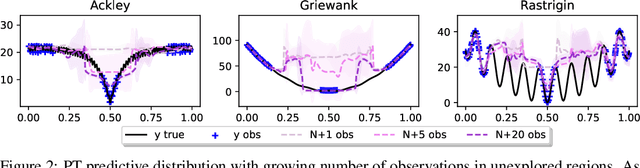
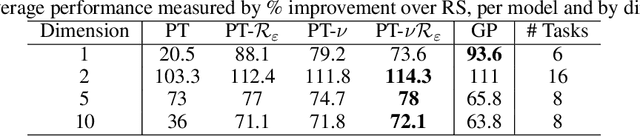
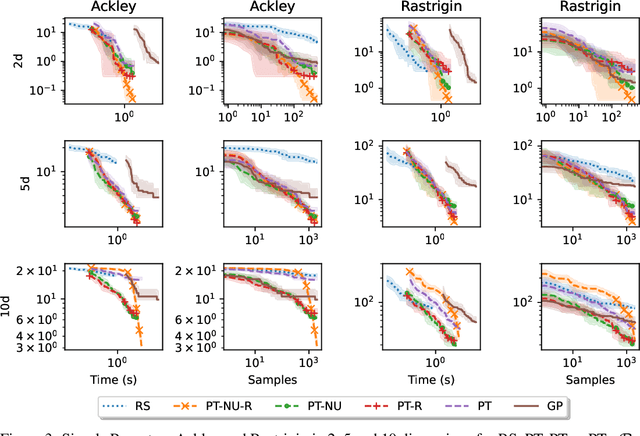
Faced with problems of increasing complexity, recent research in Bayesian Optimisation (BO) has focused on adapting deep probabilistic models as flexible alternatives to Gaussian Processes (GPs). In a similar vein, this paper investigates the feasibility of employing state-of-the-art probabilistic transformers in BO. Upon further investigation, we observe two drawbacks stemming from their training procedure and loss definition, hindering their direct deployment as proxies in black-box optimisation. First, we notice that these models are trained on uniformly distributed inputs, which impairs predictive accuracy on non-uniform data - a setting arising from any typical BO loop due to exploration-exploitation trade-offs. Second, we realise that training losses (e.g., cross-entropy) only asymptotically guarantee accurate posterior approximations, i.e., after arriving at the global optimum, which generally cannot be ensured. At the stationary points of the loss function, however, we observe a degradation in predictive performance especially in exploratory regions of the input space. To tackle these shortcomings we introduce two components: 1) a BO-tailored training prior supporting non-uniformly distributed points, and 2) a novel approximate posterior regulariser trading-off accuracy and input sensitivity to filter favourable stationary points for improved predictive performance. In a large panel of experiments, we demonstrate, for the first time, that one transformer pre-trained on data sampled from random GP priors produces competitive results on 16 benchmark black-boxes compared to GP-based BO. Since our model is only pre-trained once and used in all tasks without any retraining and/or fine-tuning, we report an order of magnitude time-reduction, while matching and sometimes outperforming GPs.

AntBO: Towards Real-World Automated Antibody Design with Combinatorial Bayesian Optimisation

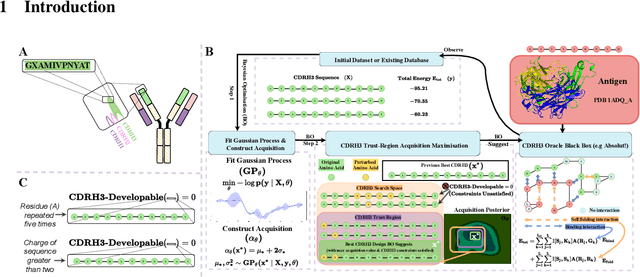
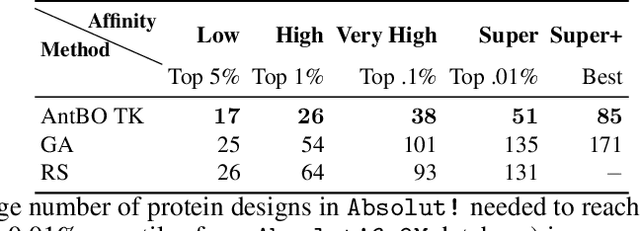
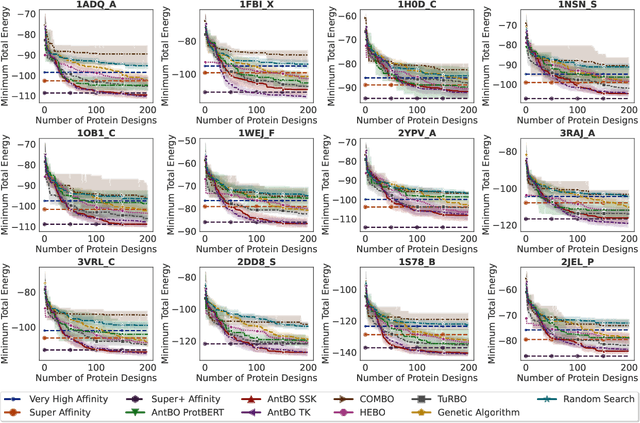
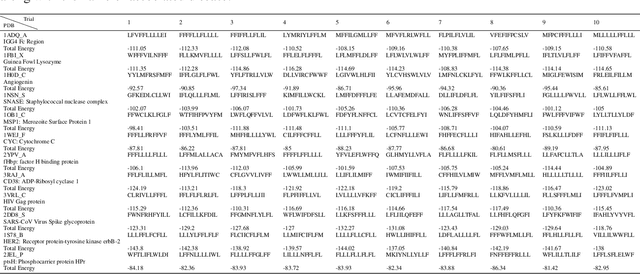
Antibodies are canonically Y-shaped multimeric proteins capable of highly specific molecular recognition. The CDRH3 region located at the tip of variable chains of an antibody dominates antigen-binding specificity. Therefore, it is a priority to design optimal antigen-specific CDRH3 regions to develop therapeutic antibodies to combat harmful pathogens. However, the combinatorial nature of CDRH3 sequence space makes it impossible to search for an optimal binding sequence exhaustively and efficiently, especially not experimentally. Here, we present AntBO: a Combinatorial Bayesian Optimisation framework enabling efficient in silico design of the CDRH3 region. Ideally, antibodies should bind to their target antigen and be free from any harmful outcomes. Therefore, we introduce the CDRH3 trust region that restricts the search to sequences with feasible developability scores. To benchmark AntBO, we use the Absolut! software suite as a black-box oracle because it can score the target specificity and affinity of designed antibodies in silico in an unconstrained fashion. The results across 188 antigens demonstrate the benefit of AntBO in designing CDRH3 regions with diverse biophysical properties. In under 200 protein designs, AntBO can suggest antibody sequences that outperform the best binding sequence drawn from 6.9 million experimentally obtained CDRH3s and a commonly used genetic algorithm baseline. Additionally, AntBO finds very-high affinity CDRH3 sequences in only 38 protein designs whilst requiring no domain knowledge. We conclude AntBO brings automated antibody design methods closer to what is practically viable for in vitro experimentation.

Self-consistent Gradient-like Eigen Decomposition in Solving Schrödinger Equations

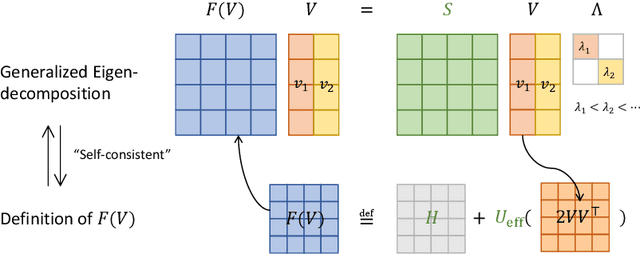
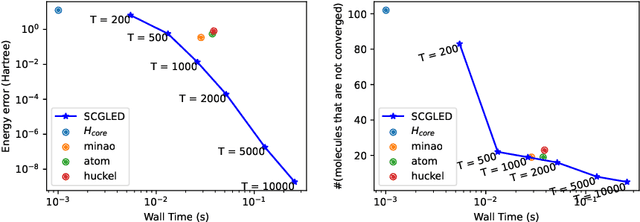
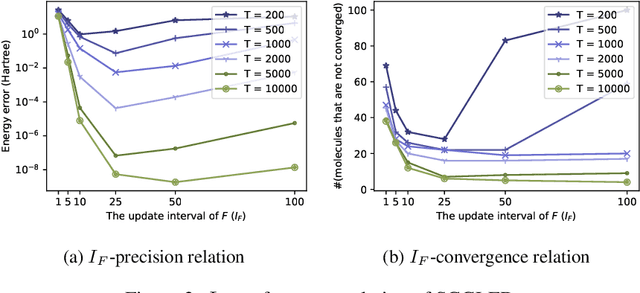
The Schr\"odinger equation is at the heart of modern quantum mechanics. Since exact solutions of the ground state are typically intractable, standard approaches approximate Schr\"odinger equation as forms of nonlinear generalized eigenvalue problems $F(V)V = SV\Lambda$ in which $F(V)$, the matrix to be decomposed, is a function of its own top-$k$ smallest eigenvectors $V$, leading to a "self-consistency problem". Traditional iterative methods heavily rely on high-quality initial guesses of $V$ generated via domain-specific heuristics methods based on quantum mechanics. In this work, we eliminate such a need for domain-specific heuristics by presenting a novel framework, Self-consistent Gradient-like Eigen Decomposition (SCGLED) that regards $F(V)$ as a special "online data generator", thus allows gradient-like eigendecomposition methods in streaming $k$-PCA to approach the self-consistency of the equation from scratch in an iterative way similar to online learning. With several critical numerical improvements, SCGLED is robust to initial guesses, free of quantum-mechanism-based heuristics designs, and neat in implementation. Our experiments show that it not only can simply replace traditional heuristics-based initial guess methods with large performance advantage (achieved averagely 25x more precise than the best baseline in similar wall time), but also is capable of finding highly precise solutions independently without any traditional iterative methods.

BOiLS: Bayesian Optimisation for Logic Synthesis

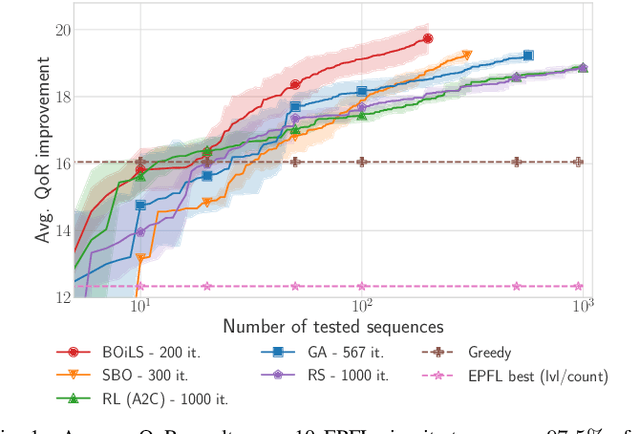
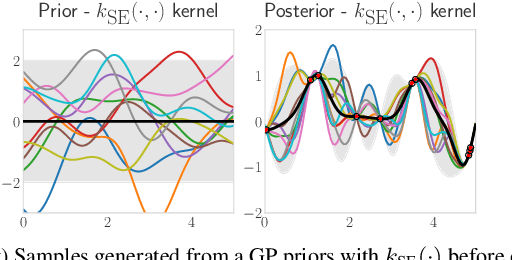
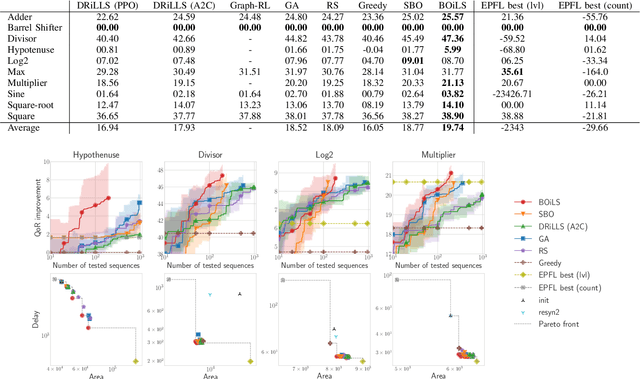
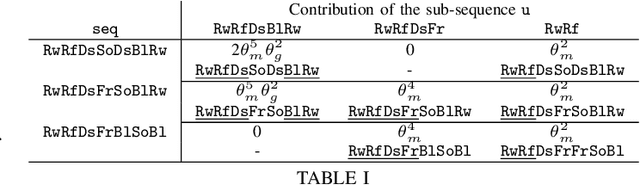
Optimising the quality-of-results (QoR) of circuits during logic synthesis is a formidable challenge necessitating the exploration of exponentially sized search spaces. While expert-designed operations aid in uncovering effective sequences, the increase in complexity of logic circuits favours automated procedures. Inspired by the successes of machine learning, researchers adapted deep learning and reinforcement learning to logic synthesis applications. However successful, those techniques suffer from high sample complexities preventing widespread adoption. To enable efficient and scalable solutions, we propose BOiLS, the first algorithm adapting modern Bayesian optimisation to navigate the space of synthesis operations. BOiLS requires no human intervention and effectively trades-off exploration versus exploitation through novel Gaussian process kernels and trust-region constrained acquisitions. In a set of experiments on EPFL benchmarks, we demonstrate BOiLS's superior performance compared to state-of-the-art in terms of both sample efficiency and QoR values.

High-Dimensional Bayesian Optimisation with Variational Autoencoders and Deep Metric Learning

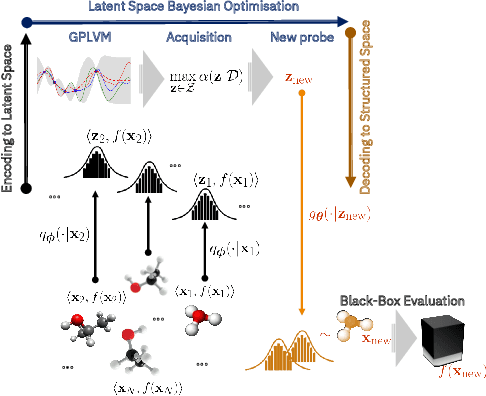
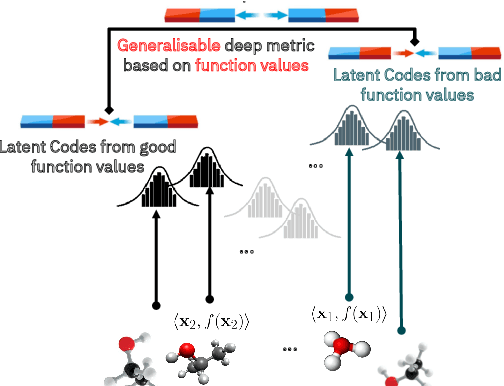
We introduce a method based on deep metric learning to perform Bayesian optimisation over high-dimensional, structured input spaces using variational autoencoders (VAEs). By extending ideas from supervised deep metric learning, we address a longstanding problem in high-dimensional VAE Bayesian optimisation, namely how to enforce a discriminative latent space as an inductive bias. Importantly, we achieve such an inductive bias using just 1% of the available labelled data relative to previous work, highlighting the sample efficiency of our approach. As a theoretical contribution, we present a proof of vanishing regret for our method. As an empirical contribution, we present state-of-the-art results on real-world high-dimensional black-box optimisation problems including property-guided molecule generation. It is the hope that the results presented in this paper can act as a guiding principle for realising effective high-dimensional Bayesian optimisation.

Efficient Semi-Implicit Variational Inference

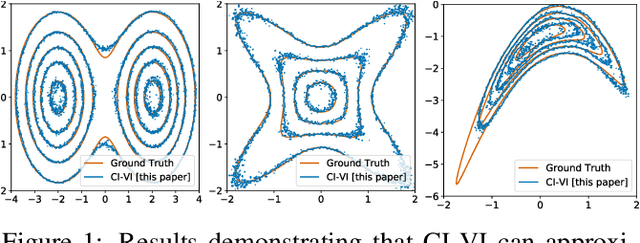
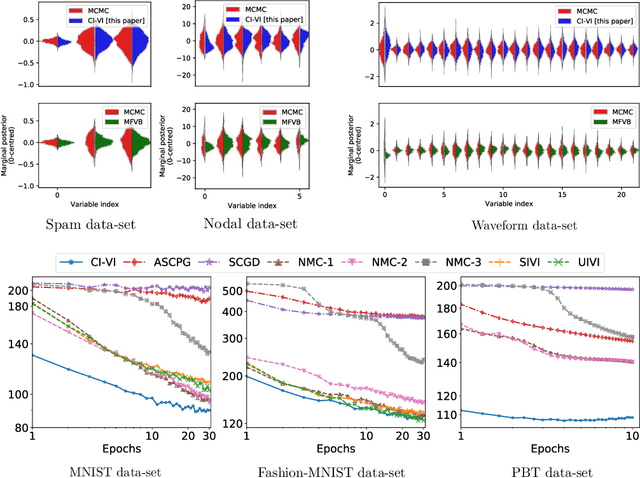
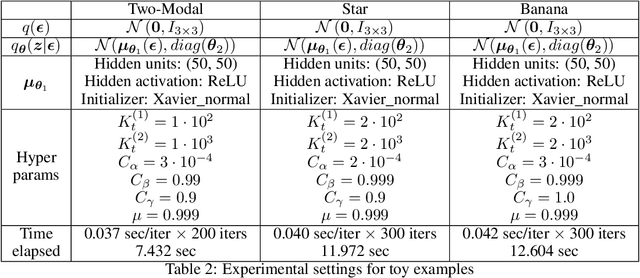
In this paper, we propose CI-VI an efficient and scalable solver for semi-implicit variational inference (SIVI). Our method, first, maps SIVI's evidence lower bound (ELBO) to a form involving a nonlinear functional nesting of expected values and then develops a rigorous optimiser capable of correctly handling bias inherent to nonlinear nested expectations using an extrapolation-smoothing mechanism coupled with gradient sketching. Our theoretical results demonstrate convergence to a stationary point of the ELBO in general non-convex settings typically arising when using deep network models and an order of $O(t^{-\frac{4}{5}})$ gradient-bias-vanishing rate. We believe these results generalise beyond the specific nesting arising from SIVI to other forms. Finally, in a set of experiments, we demonstrate the effectiveness of our algorithm in approximating complex posteriors on various data-sets including those from natural language processing.

Are we Forgetting about Compositional Optimisers in Bayesian Optimisation?

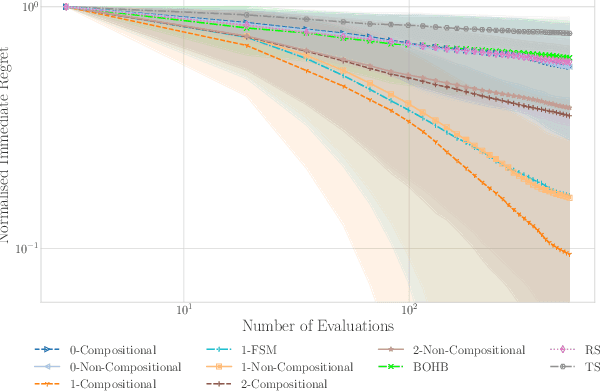
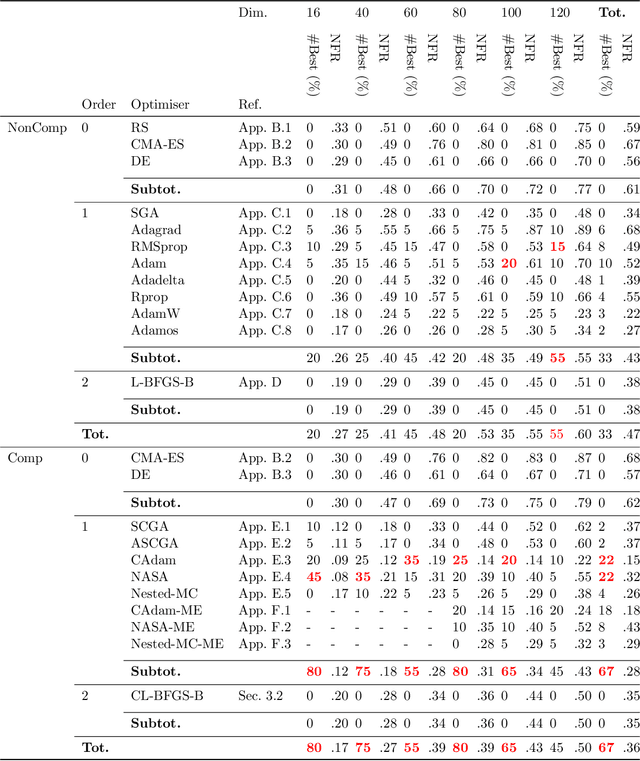
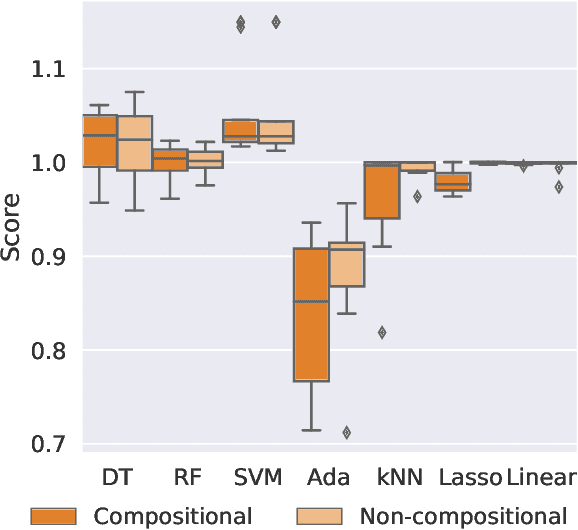
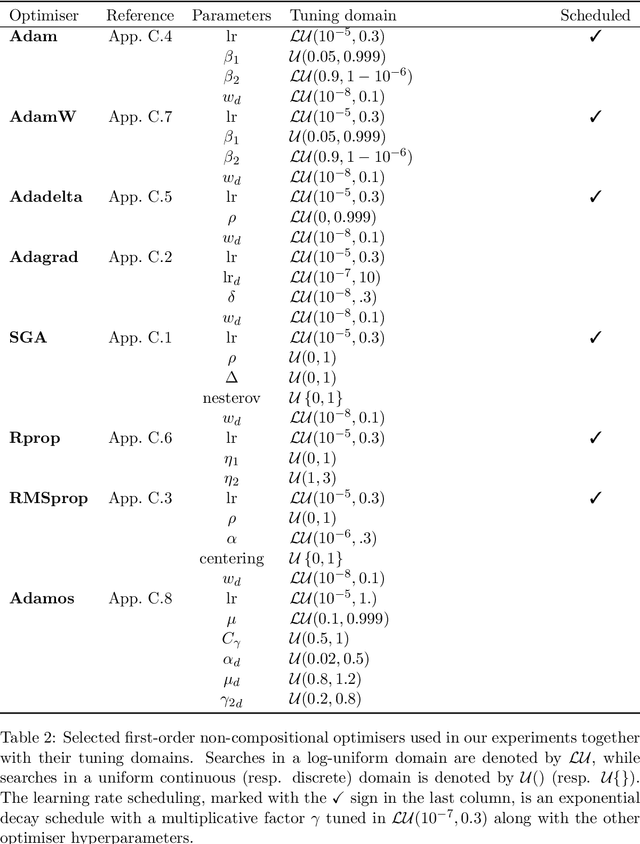
Bayesian optimisation presents a sample-efficient methodology for global optimisation. Within this framework, a crucial performance-determining subroutine is the maximisation of the acquisition function, a task complicated by the fact that acquisition functions tend to be non-convex and thus nontrivial to optimise. In this paper, we undertake a comprehensive empirical study of approaches to maximise the acquisition function. Additionally, by deriving novel, yet mathematically equivalent, compositional forms for popular acquisition functions, we recast the maximisation task as a compositional optimisation problem, allowing us to benefit from the extensive literature in this field. We highlight the empirical advantages of the compositional approach to acquisition function maximisation across 3958 individual experiments comprising synthetic optimisation tasks as well as tasks from Bayesmark. Given the generality of the acquisition function maximisation subroutine, we posit that the adoption of compositional optimisers has the potential to yield performance improvements across all domains in which Bayesian optimisation is currently being applied.

HEBO: Heteroscedastic Evolutionary Bayesian Optimisation

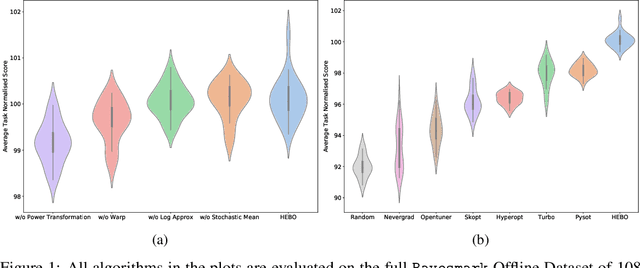
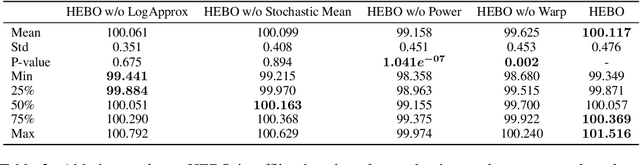
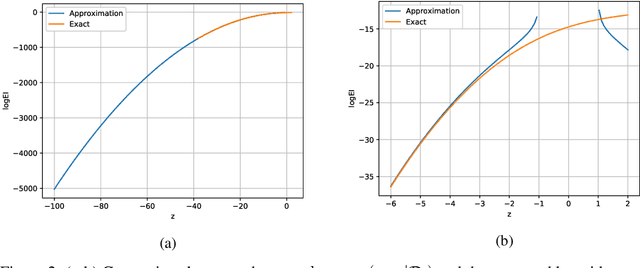
We introduce HEBO: Heteroscedastic Evolutionary Bayesian Optimisation that won the NeurIPS 2020 black-box optimisation competition. We present non-conventional modifications to the surrogate model and acquisition maximisation process and show such a combination superior against all baselines provided by the \texttt{Bayesmark} package. Lastly, we perform an ablation study to highlight the components that contributed to the success of HEBO.

Compositional ADAM: An Adaptive Compositional Solver

In this paper, we present C-ADAM, the first adaptive solver for compositional problems involving a non-linear functional nesting of expected values. We proof that C-ADAM converges to a stationary point in $\mathcal{O}(\delta^{-2.25})$ with $\delta$ being a precision parameter. Moreover, we demonstrate the importance of our results by bridging, for the first time, model-agnostic meta-learning (MAML) and compositional optimisation showing fastest known rates for deep network adaptation to-date. Finally, we validate our findings in a set of experiments from portfolio optimisation and meta-learning. Our results manifest significant sample complexity reductions compared to both standard and compositional solvers.