Are we Forgetting about Compositional Optimisers in Bayesian Optimisation?
Paper and Code
Dec 17, 2020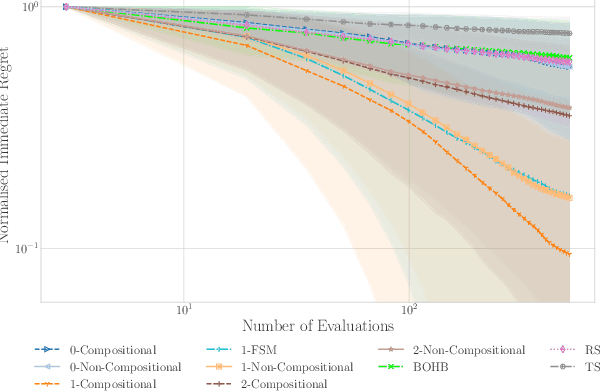
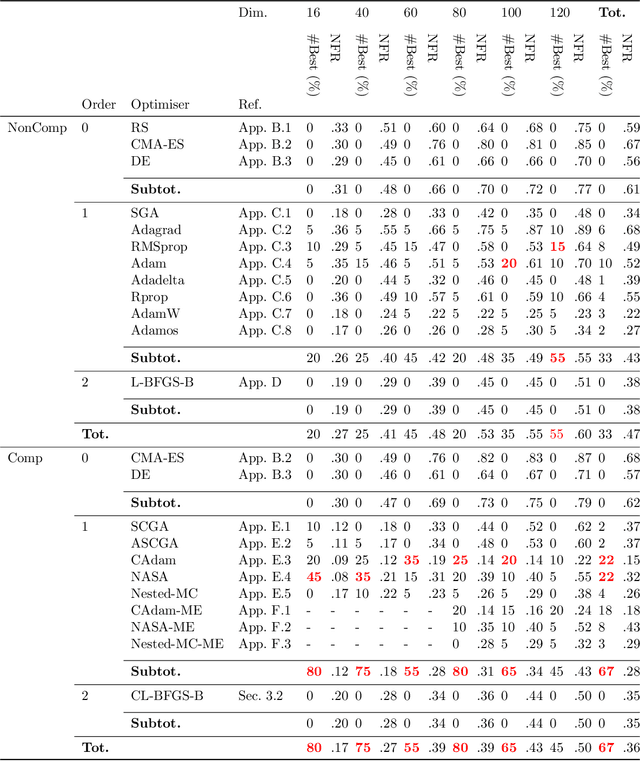
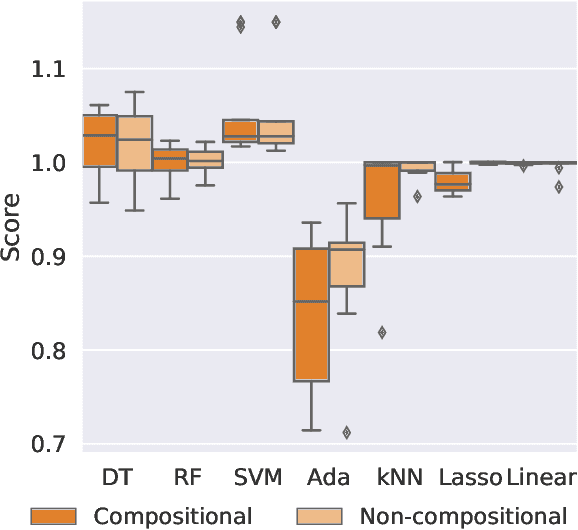
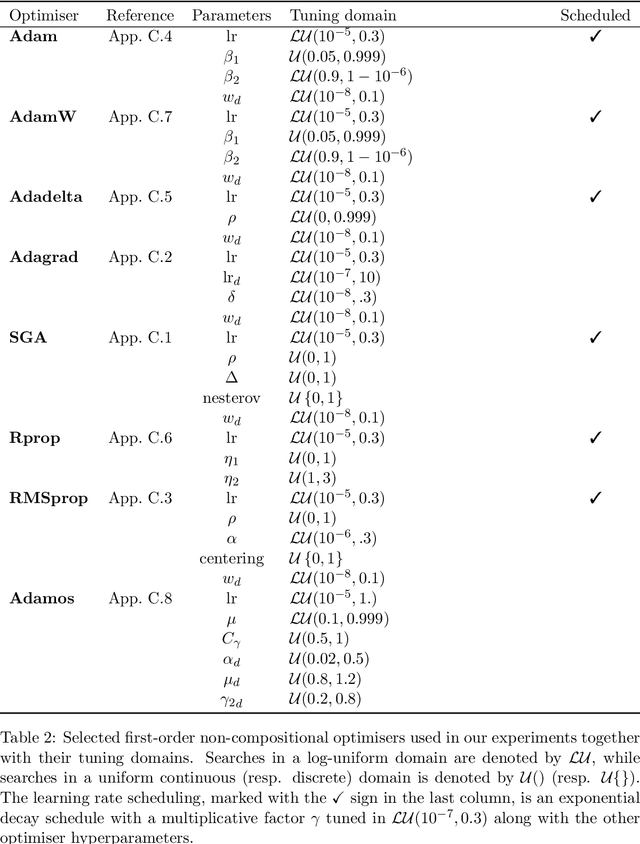
Bayesian optimisation presents a sample-efficient methodology for global optimisation. Within this framework, a crucial performance-determining subroutine is the maximisation of the acquisition function, a task complicated by the fact that acquisition functions tend to be non-convex and thus nontrivial to optimise. In this paper, we undertake a comprehensive empirical study of approaches to maximise the acquisition function. Additionally, by deriving novel, yet mathematically equivalent, compositional forms for popular acquisition functions, we recast the maximisation task as a compositional optimisation problem, allowing us to benefit from the extensive literature in this field. We highlight the empirical advantages of the compositional approach to acquisition function maximisation across 3958 individual experiments comprising synthetic optimisation tasks as well as tasks from Bayesmark. Given the generality of the acquisition function maximisation subroutine, we posit that the adoption of compositional optimisers has the potential to yield performance improvements across all domains in which Bayesian optimisation is currently being applied.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge