Self-consistent Gradient-like Eigen Decomposition in Solving Schrödinger Equations

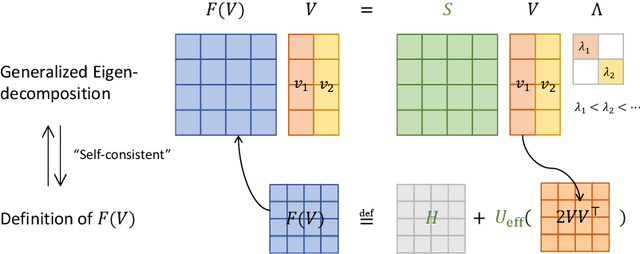
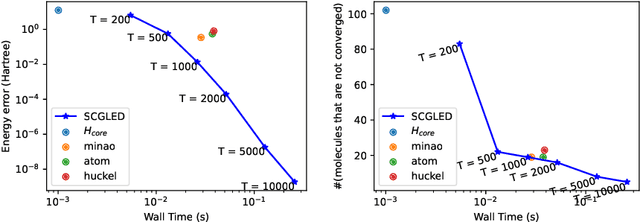
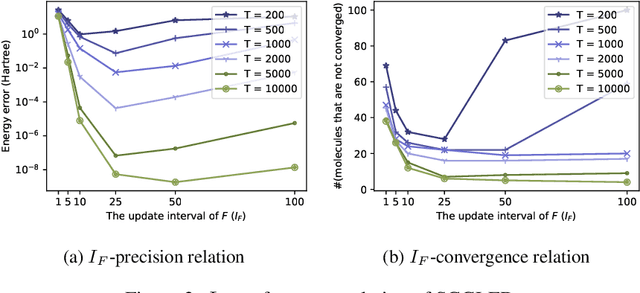
The Schr\"odinger equation is at the heart of modern quantum mechanics. Since exact solutions of the ground state are typically intractable, standard approaches approximate Schr\"odinger equation as forms of nonlinear generalized eigenvalue problems $F(V)V = SV\Lambda$ in which $F(V)$, the matrix to be decomposed, is a function of its own top-$k$ smallest eigenvectors $V$, leading to a "self-consistency problem". Traditional iterative methods heavily rely on high-quality initial guesses of $V$ generated via domain-specific heuristics methods based on quantum mechanics. In this work, we eliminate such a need for domain-specific heuristics by presenting a novel framework, Self-consistent Gradient-like Eigen Decomposition (SCGLED) that regards $F(V)$ as a special "online data generator", thus allows gradient-like eigendecomposition methods in streaming $k$-PCA to approach the self-consistency of the equation from scratch in an iterative way similar to online learning. With several critical numerical improvements, SCGLED is robust to initial guesses, free of quantum-mechanism-based heuristics designs, and neat in implementation. Our experiments show that it not only can simply replace traditional heuristics-based initial guess methods with large performance advantage (achieved averagely 25x more precise than the best baseline in similar wall time), but also is capable of finding highly precise solutions independently without any traditional iterative methods.