Large Language Models Orchestrating Structured Reasoning Achieve Kaggle Grandmaster Level

We introduce Agent K v1.0, an end-to-end autonomous data science agent designed to automate, optimise, and generalise across diverse data science tasks. Fully automated, Agent K v1.0 manages the entire data science life cycle by learning from experience. It leverages a highly flexible structured reasoning framework to enable it to dynamically process memory in a nested structure, effectively learning from accumulated experience stored to handle complex reasoning tasks. It optimises long- and short-term memory by selectively storing and retrieving key information, guiding future decisions based on environmental rewards. This iterative approach allows it to refine decisions without fine-tuning or backpropagation, achieving continuous improvement through experiential learning. We evaluate our agent's apabilities using Kaggle competitions as a case study. Following a fully automated protocol, Agent K v1.0 systematically addresses complex and multimodal data science tasks, employing Bayesian optimisation for hyperparameter tuning and feature engineering. Our new evaluation framework rigorously assesses Agent K v1.0's end-to-end capabilities to generate and send submissions starting from a Kaggle competition URL. Results demonstrate that Agent K v1.0 achieves a 92.5\% success rate across tasks, spanning tabular, computer vision, NLP, and multimodal domains. When benchmarking against 5,856 human Kaggle competitors by calculating Elo-MMR scores for each, Agent K v1.0 ranks in the top 38\%, demonstrating an overall skill level comparable to Expert-level users. Notably, its Elo-MMR score falls between the first and third quartiles of scores achieved by human Grandmasters. Furthermore, our results indicate that Agent K v1.0 has reached a performance level equivalent to Kaggle Grandmaster, with a record of 6 gold, 3 silver, and 7 bronze medals, as defined by Kaggle's progression system.

Zero-shot Model-based Reinforcement Learning using Large Language Models

The emerging zero-shot capabilities of Large Language Models (LLMs) have led to their applications in areas extending well beyond natural language processing tasks. In reinforcement learning, while LLMs have been extensively used in text-based environments, their integration with continuous state spaces remains understudied. In this paper, we investigate how pre-trained LLMs can be leveraged to predict in context the dynamics of continuous Markov decision processes. We identify handling multivariate data and incorporating the control signal as key challenges that limit the potential of LLMs' deployment in this setup and propose Disentangled In-Context Learning (DICL) to address them. We present proof-of-concept applications in two reinforcement learning settings: model-based policy evaluation and data-augmented off-policy reinforcement learning, supported by theoretical analysis of the proposed methods. Our experiments further demonstrate that our approach produces well-calibrated uncertainty estimates. We release the code at https://github.com/abenechehab/dicl.

Differentially Private Model-Based Offline Reinforcement Learning

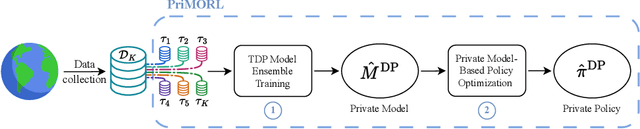
We address offline reinforcement learning with privacy guarantees, where the goal is to train a policy that is differentially private with respect to individual trajectories in the dataset. To achieve this, we introduce DP-MORL, an MBRL algorithm coming with differential privacy guarantees. A private model of the environment is first learned from offline data using DP-FedAvg, a training method for neural networks that provides differential privacy guarantees at the trajectory level. Then, we use model-based policy optimization to derive a policy from the (penalized) private model, without any further interaction with the system or access to the input data. We empirically show that DP-MORL enables the training of private RL agents from offline data and we furthermore outline the price of privacy in this setting.

Deep autoregressive density nets vs neural ensembles for model-based offline reinforcement learning

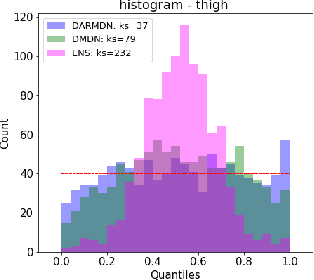
We consider the problem of offline reinforcement learning where only a set of system transitions is made available for policy optimization. Following recent advances in the field, we consider a model-based reinforcement learning algorithm that infers the system dynamics from the available data and performs policy optimization on imaginary model rollouts. This approach is vulnerable to exploiting model errors which can lead to catastrophic failures on the real system. The standard solution is to rely on ensembles for uncertainty heuristics and to avoid exploiting the model where it is too uncertain. We challenge the popular belief that we must resort to ensembles by showing that better performance can be obtained with a single well-calibrated autoregressive model on the D4RL benchmark. We also analyze static metrics of model-learning and conclude on the important model properties for the final performance of the agent.

A Multi-step Loss Function for Robust Learning of the Dynamics in Model-based Reinforcement Learning

In model-based reinforcement learning, most algorithms rely on simulating trajectories from one-step models of the dynamics learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as the length of the trajectory grows. In this paper we tackle this issue by using a multi-step objective to train one-step models. Our objective is a weighted sum of the mean squared error (MSE) loss at various future horizons. We find that this new loss is particularly useful when the data is noisy (additive Gaussian noise in the observations), which is often the case in real-life environments. To support the multi-step loss, first we study its properties in two tractable cases: i) uni-dimensional linear system, and ii) two-parameter non-linear system. Second, we show in a variety of tasks (environments or datasets) that the models learned with this loss achieve a significant improvement in terms of the averaged R2-score on future prediction horizons. Finally, in the pure batch reinforcement learning setting, we demonstrate that one-step models serve as strong baselines when dynamics are deterministic, while multi-step models would be more advantageous in the presence of noise, highlighting the potential of our approach in real-world applications.

Multi-timestep models for Model-based Reinforcement Learning

In model-based reinforcement learning (MBRL), most algorithms rely on simulating trajectories from one-step dynamics models learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as length of the trajectory grows. In this paper we tackle this issue by using a multi-timestep objective to train one-step models. Our objective is a weighted sum of a loss function (e.g., negative log-likelihood) at various future horizons. We explore and test a range of weights profiles. We find that exponentially decaying weights lead to models that significantly improve the long-horizon R2 score. This improvement is particularly noticeable when the models were evaluated on noisy data. Finally, using a soft actor-critic (SAC) agent in pure batch reinforcement learning (RL) and iterated batch RL scenarios, we found that our multi-timestep models outperform or match standard one-step models. This was especially evident in a noisy variant of the considered environment, highlighting the potential of our approach in real-world applications.

Guided Safe Shooting: model based reinforcement learning with safety constraints

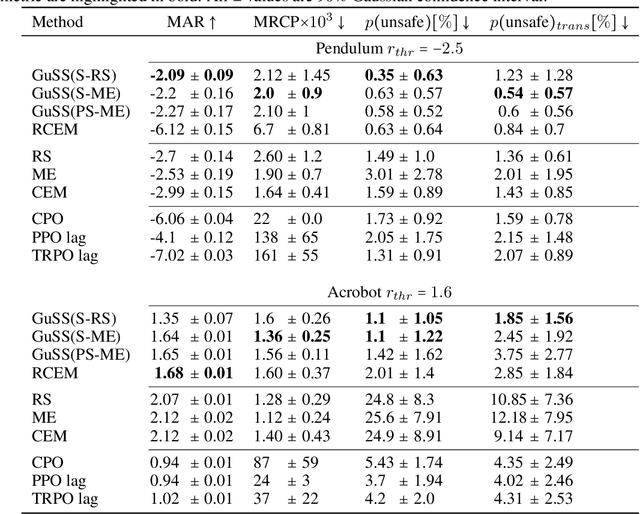
In the last decade, reinforcement learning successfully solved complex control tasks and decision-making problems, like the Go board game. Yet, there are few success stories when it comes to deploying those algorithms to real-world scenarios. One of the reasons is the lack of guarantees when dealing with and avoiding unsafe states, a fundamental requirement in critical control engineering systems. In this paper, we introduce Guided Safe Shooting (GuSS), a model-based RL approach that can learn to control systems with minimal violations of the safety constraints. The model is learned on the data collected during the operation of the system in an iterated batch fashion, and is then used to plan for the best action to perform at each time step. We propose three different safe planners, one based on a simple random shooting strategy and two based on MAP-Elites, a more advanced divergent-search algorithm. Experiments show that these planners help the learning agent avoid unsafe situations while maximally exploring the state space, a necessary aspect when learning an accurate model of the system. Furthermore, compared to model-free approaches, learning a model allows GuSS reducing the number of interactions with the real-system while still reaching high rewards, a fundamental requirement when handling engineering systems.

An $α$-No-Regret Algorithm For Graphical Bilinear Bandits

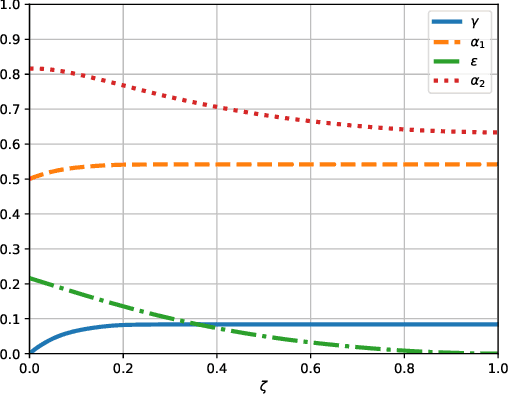
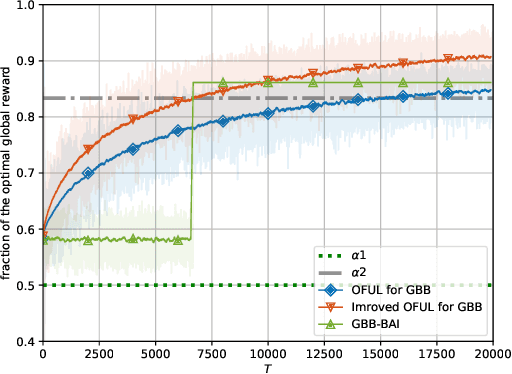
We propose the first regret-based approach to the Graphical Bilinear Bandits problem, where $n$ agents in a graph play a stochastic bilinear bandit game with each of their neighbors. This setting reveals a combinatorial NP-hard problem that prevents the use of any existing regret-based algorithm in the (bi-)linear bandit literature. In this paper, we fill this gap and present the first regret-based algorithm for graphical bilinear bandits using the principle of optimism in the face of uncertainty. Theoretical analysis of this new method yields an upper bound of $\tilde{O}(\sqrt{T})$ on the $\alpha$-regret and evidences the impact of the graph structure on the rate of convergence. Finally, we show through various experiments the validity of our approach.

Model-based micro-data reinforcement learning: what are the crucial model properties and which model to choose?

We contribute to micro-data model-based reinforcement learning (MBRL) by rigorously comparing popular generative models using a fixed (random shooting) control agent. We find that on an environment that requires multimodal posterior predictives, mixture density nets outperform all other models by a large margin. When multimodality is not required, our surprising finding is that we do not need probabilistic posterior predictives: deterministic models are on par, in fact they consistently (although non-significantly) outperform their probabilistic counterparts. We also found that heteroscedasticity at training time, perhaps acting as a regularizer, improves predictions at longer horizons. At the methodological side, we design metrics and an experimental protocol which can be used to evaluate the various models, predicting their asymptotic performance when using them on the control problem. Using this framework, we improve the state-of-the-art sample complexity of MBRL on Acrobot by two to four folds, using an aggressive training schedule which is outside of the hyperparameter interval usually considered

Refined bounds for randomized experimental design

Experimental design is an approach for selecting samples among a given set so as to obtain the best estimator for a given criterion. In the context of linear regression, several optimal designs have been derived, each associated with a different criterion: mean square error, robustness, \emph{etc}. Computing such designs is generally an NP-hard problem and one can instead rely on a convex relaxation that considers probability distributions over the samples. Although greedy strategies and rounding procedures have received a lot of attention, straightforward sampling from the optimal distribution has hardly been investigated. In this paper, we propose theoretical guarantees for randomized strategies on E and G-optimal design. To this end, we develop a new concentration inequality for the eigenvalues of random matrices using a refined version of the intrinsic dimension that enables us to quantify the performance of such randomized strategies. Finally, we evidence the validity of our analysis through experiments, with particular attention on the G-optimal design applied to the best arm identification problem for linear bandits.