An $α$-No-Regret Algorithm For Graphical Bilinear Bandits

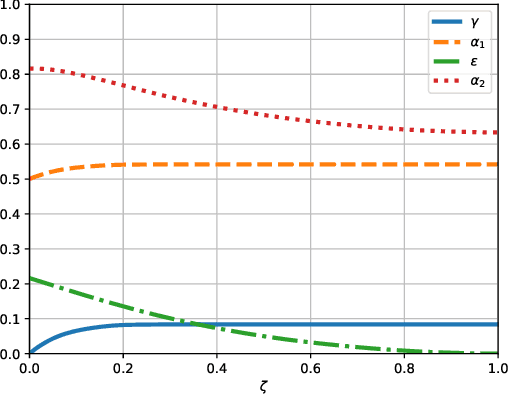
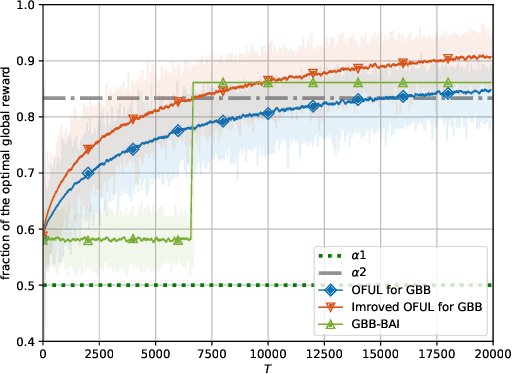
We propose the first regret-based approach to the Graphical Bilinear Bandits problem, where $n$ agents in a graph play a stochastic bilinear bandit game with each of their neighbors. This setting reveals a combinatorial NP-hard problem that prevents the use of any existing regret-based algorithm in the (bi-)linear bandit literature. In this paper, we fill this gap and present the first regret-based algorithm for graphical bilinear bandits using the principle of optimism in the face of uncertainty. Theoretical analysis of this new method yields an upper bound of $\tilde{O}(\sqrt{T})$ on the $\alpha$-regret and evidences the impact of the graph structure on the rate of convergence. Finally, we show through various experiments the validity of our approach.

Learning in nonatomic games, Part I: Finite action spaces and population games

We examine the long-run behavior of a wide range of dynamics for learning in nonatomic games, in both discrete and continuous time. The class of dynamics under consideration includes fictitious play and its regularized variants, the best-reply dynamics (again, possibly regularized), as well as the dynamics of dual averaging / "follow the regularized leader" (which themselves include as special cases the replicator dynamics and Friedman's projection dynamics). Our analysis concerns both the actual trajectory of play and its time-average, and we cover potential and monotone games, as well as games with an evolutionarily stable state (global or otherwise). We focus exclusively on games with finite action spaces; nonatomic games with continuous action spaces are treated in detail in Part II of this paper.

Best Arm Identification in Graphical Bilinear Bandits

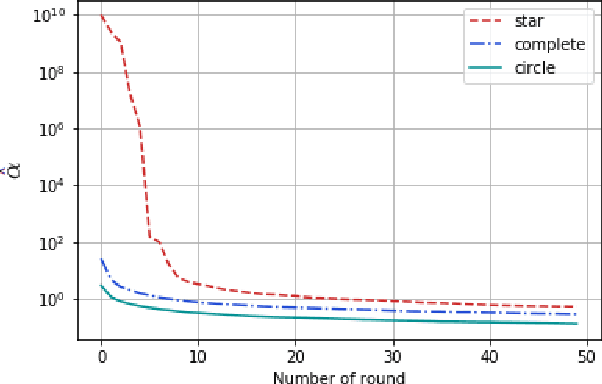
We introduce a new graphical bilinear bandit problem where a learner (or a \emph{central entity}) allocates arms to the nodes of a graph and observes for each edge a noisy bilinear reward representing the interaction between the two end nodes. We study the best arm identification problem in which the learner wants to find the graph allocation maximizing the sum of the bilinear rewards. By efficiently exploiting the geometry of this bandit problem, we propose a somehow \emph{decentralized} allocation strategy based on random sampling with theoretical guarantees. In particular, we characterize the influence of the graph structure (e.g. star, complete or circle) on the convergence rate and propose empirical experiments that confirm this dependency.

NGO-GM: Natural Gradient Optimization for Graphical Models

This paper deals with estimating model parameters in graphical models. We reformulate it as an information geometric optimization problem and introduce a natural gradient descent strategy that incorporates additional meta parameters. We show that our approach is a strong alternative to the celebrated EM approach for learning in graphical models. Actually, our natural gradient based strategy leads to learning optimal parameters for the final objective function without artificially trying to fit a distribution that may not correspond to the real one. We support our theoretical findings with the question of trend detection in financial markets and show that the learned model performs better than traditional practitioner methods and is less prone to overfitting.

A discrete version of CMA-ES

Modern machine learning uses more and more advanced optimization techniques to find optimal hyper parameters. Whenever the objective function is non-convex, non continuous and with potentially multiple local minima, standard gradient descent optimization methods fail. A last resource and very different method is to assume that the optimum(s), not necessarily unique, is/are distributed according to a distribution and iteratively to adapt the distribution according to tested points. These strategies originated in the early 1960s, named Evolution Strategy (ES) have culminated with the CMA-ES (Covariance Matrix Adaptation) ES. It relies on a multi variate normal distribution and is supposed to be state of the art for general optimization program. However, it is far from being optimal for discrete variables. In this paper, we extend the method to multivariate binomial correlated distributions. For such a distribution, we show that it shares similar features to the multi variate normal: independence and correlation is equivalent and correlation is efficiently modeled by interaction between different variables. We discuss this distribution in the framework of the exponential family. We prove that the model can estimate not only pairwise interactions among the two variables but also is capable of modeling higher order interactions. This allows creating a version of CMA ES that can accommodate efficiently discrete variables. We provide the corresponding algorithm and conclude.

Approachability of convex sets in generalized quitting games

We consider Blackwell approachability, a very powerful and geometric tool in game theory, used for example to design strategies of the uninformed player in repeated games with incomplete information. We extend this theory to "generalized quitting games" , a class of repeated stochastic games in which each player may have quitting actions, such as the Big-Match. We provide three simple geometric and strongly related conditions for the weak approachability of a convex target set. The first is sufficient: it guarantees that, for any fixed horizon, a player has a strategy ensuring that the expected time-average payoff vector converges to the target set as horizon goes to infinity. The third is necessary: if it is not satisfied, the opponent can weakly exclude the target set. In the special case where only the approaching player can quit the game (Big-Match of type I), the three conditions are equivalent and coincide with Blackwell's condition. Consequently, we obtain a full characterization and prove that the game is weakly determined-every convex set is either weakly approachable or weakly excludable. In games where only the opponent can quit (Big-Match of type II), none of our conditions is both sufficient and necessary for weak approachability. We provide a continuous time sufficient condition using techniques coming from differential games, and show its usefulness in practice, in the spirit of Vieille's seminal work for weak approachability.Finally, we study uniform approachability where the strategy should not depend on the horizon and demonstrate that, in contrast with classical Blackwell approacha-bility for convex sets, weak approachability does not imply uniform approachability.