Uncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework

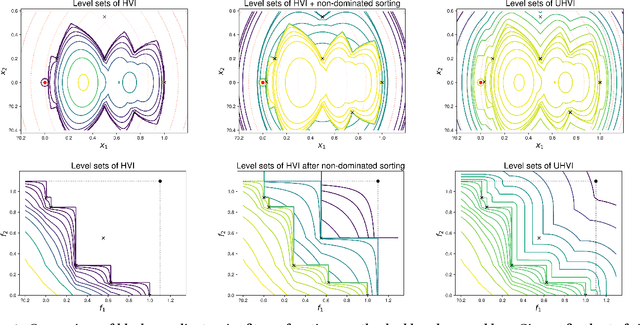
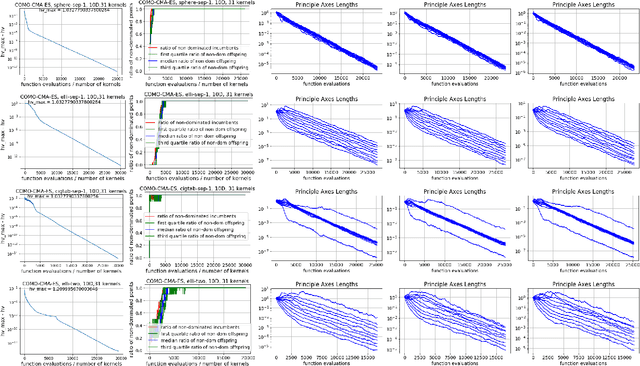
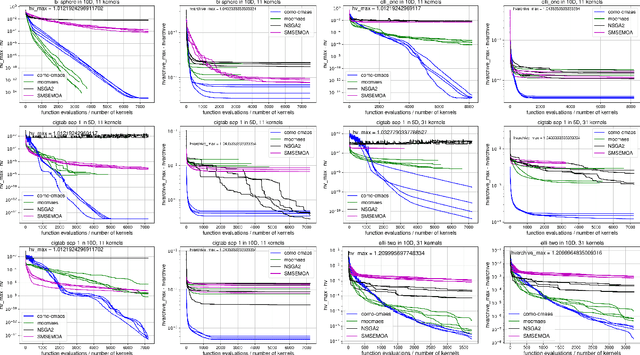
We present a framework to build a multiobjective algorithm from single-objective ones. This framework addresses the $p \times n$-dimensional problem of finding p solutions in an n-dimensional search space, maximizing an indicator by dynamic subspace optimization. Each single-objective algorithm optimizes the indicator function given $p - 1$ fixed solutions. Crucially, dominated solutions minimize their distance to the empirical Pareto front defined by these $p - 1$ solutions. We instantiate the framework with CMA-ES as single-objective optimizer. The new algorithm, COMO-CMA-ES, is empirically shown to converge linearly on bi-objective convex-quadratic problems and is compared to MO-CMA-ES, NSGA-II and SMS-EMOA.

COCO: The Large Scale Black-Box Optimization Benchmarking Test Suite

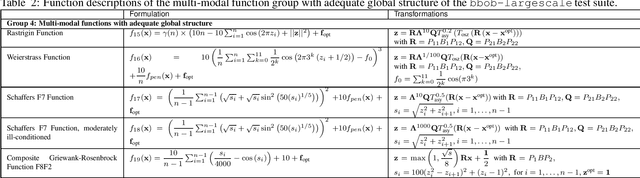
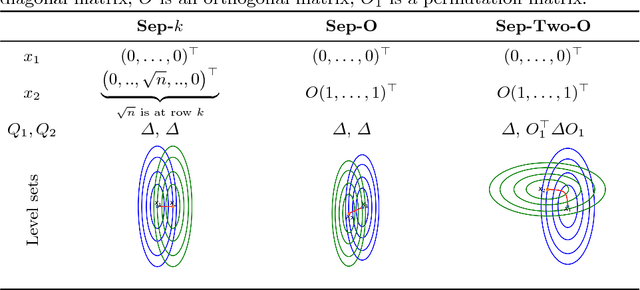
The bbob-largescale test suite, containing 24 single-objective functions in continuous domain, extends the well-known single-objective noiseless bbob test suite, which has been used since 2009 in the BBOB workshop series, to large dimension. The core idea is to make the rotational transformations R, Q in search space that appear in the bbob test suite computationally cheaper while retaining some desired properties. This documentation presents an approach that replaces a full rotational transformation with a combination of a block-diagonal matrix and two permutation matrices in order to construct test functions whose computational and memory costs scale linearly in the dimension of the problem.

A discrete version of CMA-ES

Modern machine learning uses more and more advanced optimization techniques to find optimal hyper parameters. Whenever the objective function is non-convex, non continuous and with potentially multiple local minima, standard gradient descent optimization methods fail. A last resource and very different method is to assume that the optimum(s), not necessarily unique, is/are distributed according to a distribution and iteratively to adapt the distribution according to tested points. These strategies originated in the early 1960s, named Evolution Strategy (ES) have culminated with the CMA-ES (Covariance Matrix Adaptation) ES. It relies on a multi variate normal distribution and is supposed to be state of the art for general optimization program. However, it is far from being optimal for discrete variables. In this paper, we extend the method to multivariate binomial correlated distributions. For such a distribution, we show that it shares similar features to the multi variate normal: independence and correlation is equivalent and correlation is efficiently modeled by interaction between different variables. We discuss this distribution in the framework of the exponential family. We prove that the model can estimate not only pairwise interactions among the two variables but also is capable of modeling higher order interactions. This allows creating a version of CMA ES that can accommodate efficiently discrete variables. We provide the corresponding algorithm and conclude.

On Bi-Objective convex-quadratic problems

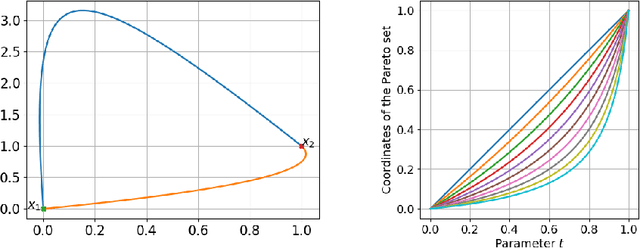
In this paper we analyze theoretical properties of bi-objective convex-quadratic problems. We give a complete description of their Pareto set and prove the convexity of their Pareto front. We show that the Pareto set is a line segment when both Hessian matrices are proportional. We then propose a novel set of convex-quadratic test problems, describe their theoretical properties and the algorithm abilities required by those test problems. This includes in particular testing the sensitivity with respect to separability, ill-conditioned problems, rotational invariance, and whether the Pareto set is aligned with the coordinate axis.

Drift Theory in Continuous Search Spaces: Expected Hitting Time of the (1+1)-ES with 1/5 Success Rule

This paper explores the use of the standard approach for proving runtime bounds in discrete domains---often referred to as drift analysis---in the context of optimization on a continuous domain. Using this framework we analyze the (1+1) Evolution Strategy with one-fifth success rule on the sphere function. To deal with potential functions that are not lower-bounded, we formulate novel drift theorems. We then use the theorems to prove bounds on the expected hitting time to reach a certain target fitness in finite dimension $d$. The bounds are akin to linear convergence. We then study the dependency of the different terms on $d$ proving a convergence rate dependency of $\Theta(1/d)$. Our results constitute the first non-asymptotic analysis for the algorithm considered as well as the first explicit application of drift analysis to a randomized search heuristic with continuous domain.

COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting

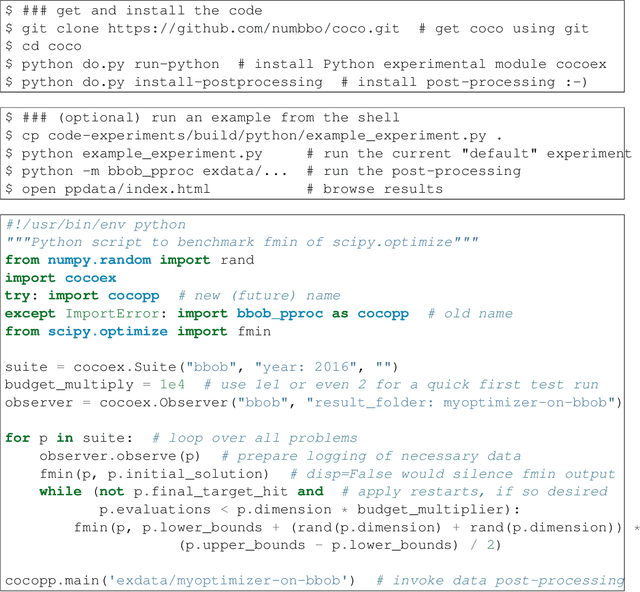
COCO is a platform for Comparing Continuous Optimizers in a black-box setting. It aims at automatizing the tedious and repetitive task of benchmarking numerical optimization algorithms to the greatest possible extent. We present the rationals behind the development of the platform as a general proposition for a guideline towards better benchmarking. We detail underlying fundamental concepts of COCO such as its definition of a problem, the idea of instances, the relevance of target values, and runtime as central performance measure. Finally, we give a quick overview of the basic code structure and the available test suites.

COCO: The Bi-objective Black Box Optimization Benchmarking Test Suite

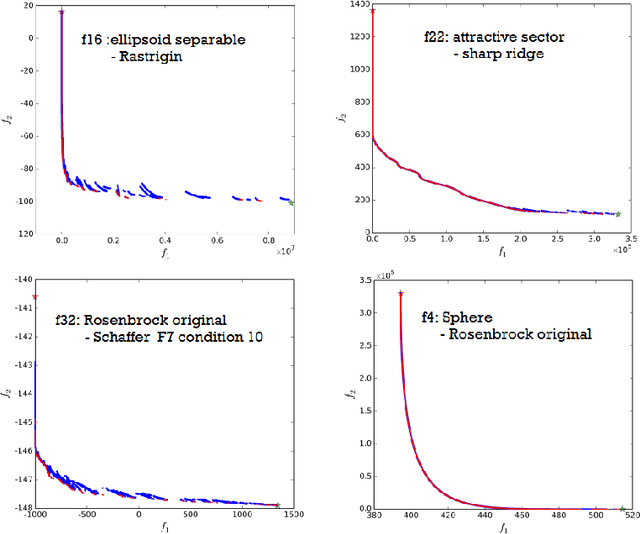
The bbob-biobj test suite contains 55 bi-objective functions in continuous domain which are derived from combining functions of the well-known single-objective noiseless bbob test suite. Besides giving the actual function definitions and presenting their (known) properties, this documentation also aims at giving the rationale behind our approach in terms of function groups, instances, and potential objective space normalization.

COCO: The Experimental Procedure

We present a budget-free experimental setup and procedure for benchmarking numericaloptimization algorithms in a black-box scenario. This procedure can be applied with the COCO benchmarking platform. We describe initialization of and input to the algorithm and touch upon therelevance of termination and restarts.

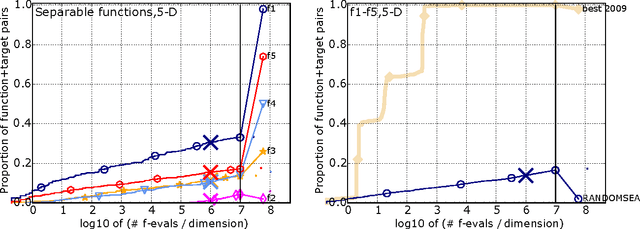
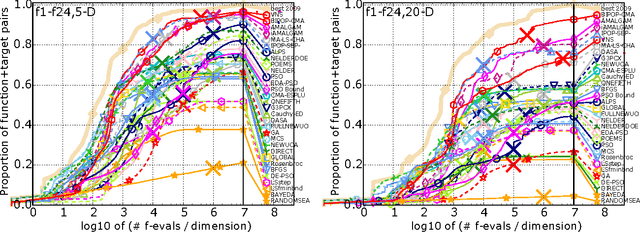
COCO: Performance Assessment

We present an any-time performance assessment for benchmarking numerical optimization algorithms in a black-box scenario, applied within the COCO benchmarking platform. The performance assessment is based on runtimes measured in number of objective function evaluations to reach one or several quality indicator target values. We argue that runtime is the only available measure with a generic, meaningful, and quantitative interpretation. We discuss the choice of the target values, runlength-based targets, and the aggregation of results by using simulated restarts, averages, and empirical distribution functions.

Biobjective Performance Assessment with the COCO Platform

This document details the rationales behind assessing the performance of numerical black-box optimizers on multi-objective problems within the COCO platform and in particular on the biobjective test suite bbob-biobj. The evaluation is based on a hypervolume of all non-dominated solutions in the archive of candidate solutions and measures the runtime until the hypervolume value succeeds prescribed target values.