Dimo Brockhoff
RANDOPT
Uncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework
Apr 18, 2019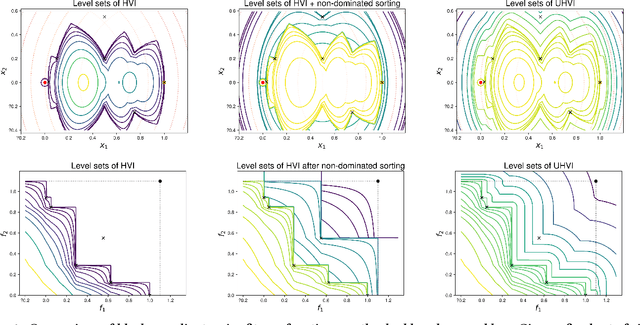

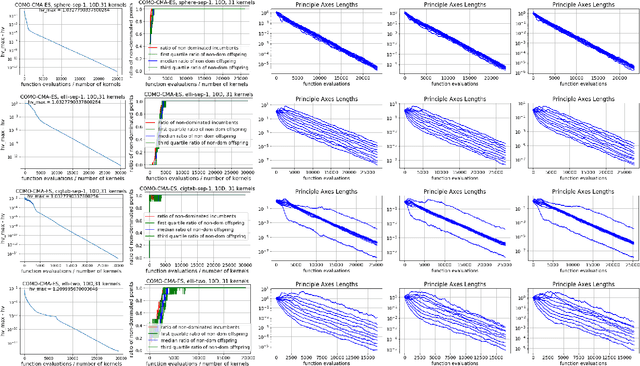
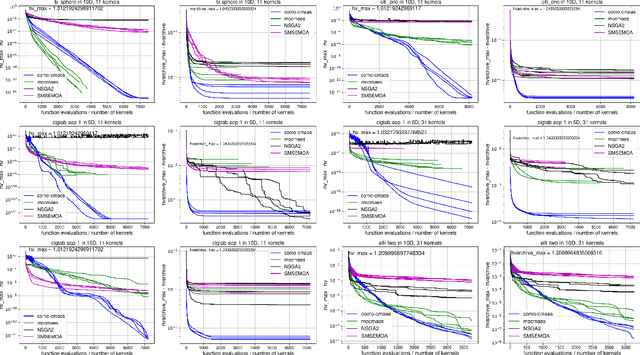
Abstract:We present a framework to build a multiobjective algorithm from single-objective ones. This framework addresses the $p \times n$-dimensional problem of finding p solutions in an n-dimensional search space, maximizing an indicator by dynamic subspace optimization. Each single-objective algorithm optimizes the indicator function given $p - 1$ fixed solutions. Crucially, dominated solutions minimize their distance to the empirical Pareto front defined by these $p - 1$ solutions. We instantiate the framework with CMA-ES as single-objective optimizer. The new algorithm, COMO-CMA-ES, is empirically shown to converge linearly on bi-objective convex-quadratic problems and is compared to MO-CMA-ES, NSGA-II and SMS-EMOA.
COCO: The Large Scale Black-Box Optimization Benchmarking Test Suite
Mar 28, 2019
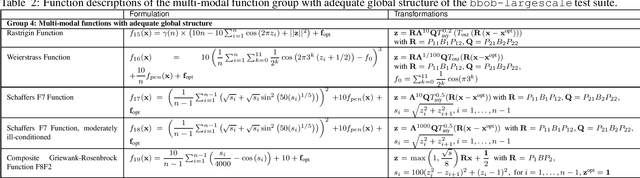

Abstract:The bbob-largescale test suite, containing 24 single-objective functions in continuous domain, extends the well-known single-objective noiseless bbob test suite, which has been used since 2009 in the BBOB workshop series, to large dimension. The core idea is to make the rotational transformations R, Q in search space that appear in the bbob test suite computationally cheaper while retaining some desired properties. This documentation presents an approach that replaces a full rotational transformation with a combination of a block-diagonal matrix and two permutation matrices in order to construct test functions whose computational and memory costs scale linearly in the dimension of the problem.
On Bi-Objective convex-quadratic problems
Dec 01, 2018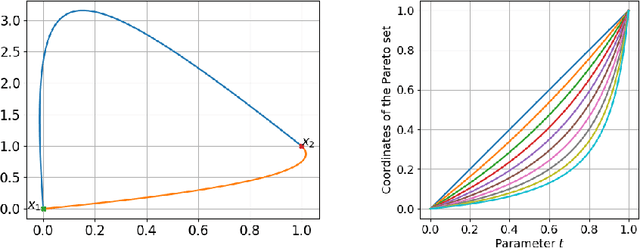


Abstract:In this paper we analyze theoretical properties of bi-objective convex-quadratic problems. We give a complete description of their Pareto set and prove the convexity of their Pareto front. We show that the Pareto set is a line segment when both Hessian matrices are proportional. We then propose a novel set of convex-quadratic test problems, describe their theoretical properties and the algorithm abilities required by those test problems. This includes in particular testing the sensitivity with respect to separability, ill-conditioned problems, rotational invariance, and whether the Pareto set is aligned with the coordinate axis.
COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting
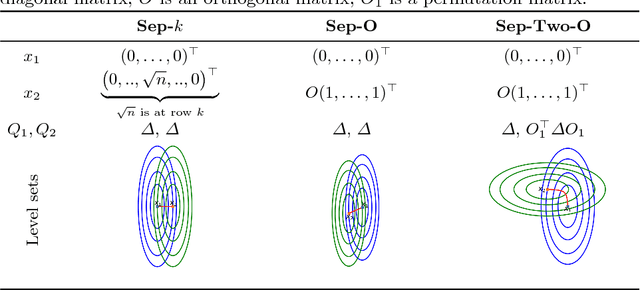
Aug 01, 2016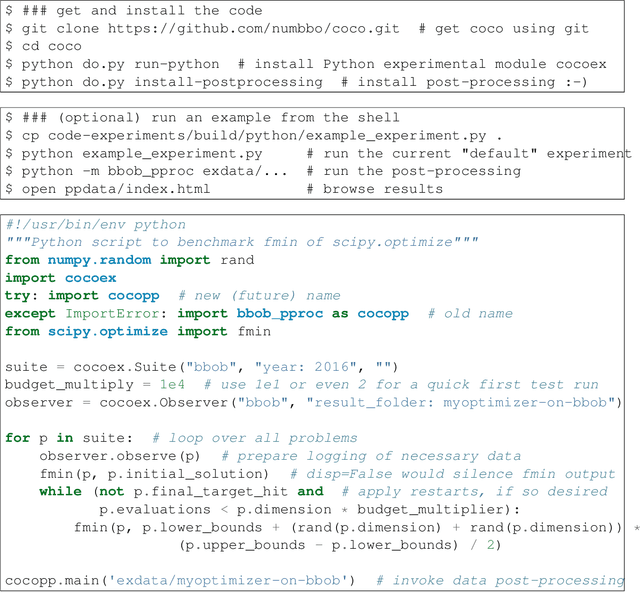
Abstract:COCO is a platform for Comparing Continuous Optimizers in a black-box setting. It aims at automatizing the tedious and repetitive task of benchmarking numerical optimization algorithms to the greatest possible extent. We present the rationals behind the development of the platform as a general proposition for a guideline towards better benchmarking. We detail underlying fundamental concepts of COCO such as its definition of a problem, the idea of instances, the relevance of target values, and runtime as central performance measure. Finally, we give a quick overview of the basic code structure and the available test suites.
COCO: The Bi-objective Black Box Optimization Benchmarking Test Suite
May 25, 2016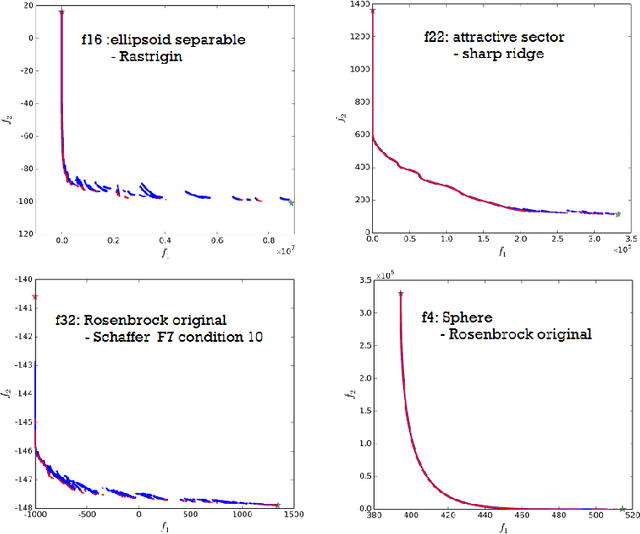
Abstract:The bbob-biobj test suite contains 55 bi-objective functions in continuous domain which are derived from combining functions of the well-known single-objective noiseless bbob test suite. Besides giving the actual function definitions and presenting their (known) properties, this documentation also aims at giving the rationale behind our approach in terms of function groups, instances, and potential objective space normalization.
COCO: The Experimental Procedure
May 19, 2016Abstract:We present a budget-free experimental setup and procedure for benchmarking numericaloptimization algorithms in a black-box scenario. This procedure can be applied with the COCO benchmarking platform. We describe initialization of and input to the algorithm and touch upon therelevance of termination and restarts.
COCO: Performance Assessment
May 11, 2016

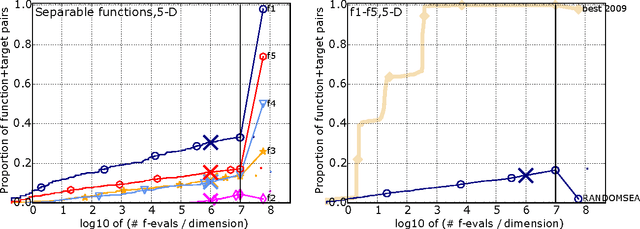
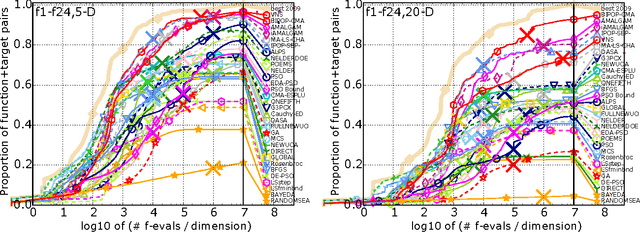
Abstract:We present an any-time performance assessment for benchmarking numerical optimization algorithms in a black-box scenario, applied within the COCO benchmarking platform. The performance assessment is based on runtimes measured in number of objective function evaluations to reach one or several quality indicator target values. We argue that runtime is the only available measure with a generic, meaningful, and quantitative interpretation. We discuss the choice of the target values, runlength-based targets, and the aggregation of results by using simulated restarts, averages, and empirical distribution functions.
Biobjective Performance Assessment with the COCO Platform
May 05, 2016

Abstract:This document details the rationales behind assessing the performance of numerical black-box optimizers on multi-objective problems within the COCO platform and in particular on the biobjective test suite bbob-biobj. The evaluation is based on a hypervolume of all non-dominated solutions in the archive of candidate solutions and measures the runtime until the hypervolume value succeeds prescribed target values.
On the Impact of Multiobjective Scalarizing Functions
Sep 19, 2014
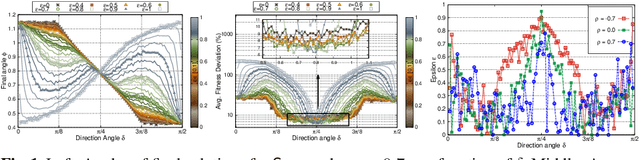

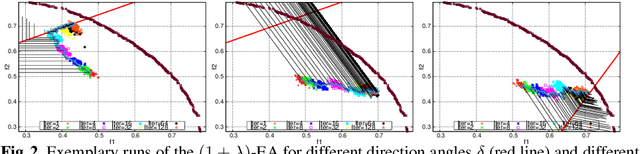
Abstract:Recently, there has been a renewed interest in decomposition-based approaches for evolutionary multiobjective optimization. However, the impact of the choice of the underlying scalarizing function(s) is still far from being well understood. In this paper, we investigate the behavior of different scalarizing functions and their parameters. We thereby abstract firstly from any specific algorithm and only consider the difficulty of the single scalarized problems in terms of the search ability of a (1+lambda)-EA on biobjective NK-landscapes. Secondly, combining the outcomes of independent single-objective runs allows for more general statements on set-based performance measures. Finally, we investigate the correlation between the opening angle of the scalarizing function's underlying contour lines and the position of the final solution in the objective space. Our analysis is of fundamental nature and sheds more light on the key characteristics of multiobjective scalarizing functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge