Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Cheikh Touré
Uncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework
Apr 18, 2019Figures and Tables: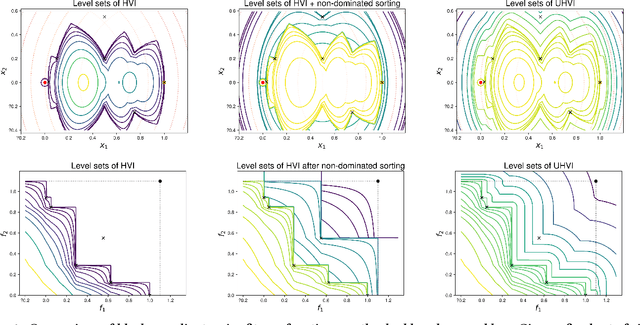

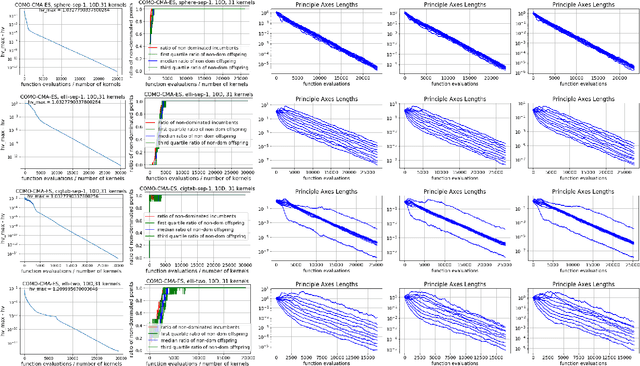
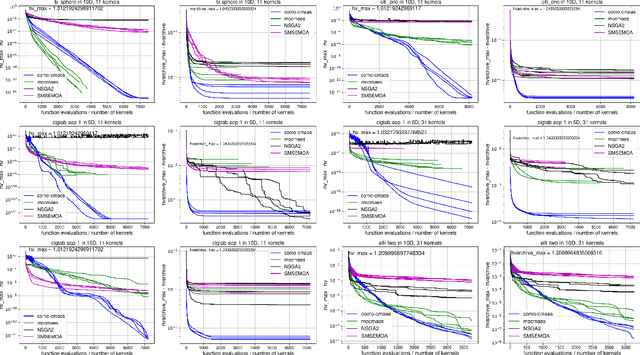




Abstract:We present a framework to build a multiobjective algorithm from single-objective ones. This framework addresses the $p \times n$-dimensional problem of finding p solutions in an n-dimensional search space, maximizing an indicator by dynamic subspace optimization. Each single-objective algorithm optimizes the indicator function given $p - 1$ fixed solutions. Crucially, dominated solutions minimize their distance to the empirical Pareto front defined by these $p - 1$ solutions. We instantiate the framework with CMA-ES as single-objective optimizer. The new algorithm, COMO-CMA-ES, is empirically shown to converge linearly on bi-objective convex-quadratic problems and is compared to MO-CMA-ES, NSGA-II and SMS-EMOA.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge