Diagonal Acceleration for Covariance Matrix Adaptation Evolution Strategies

We introduce an acceleration for covariance matrix adaptation evolution strategies (CMA-ES) by means of adaptive diagonal decoding (dd-CMA). This diagonal acceleration endows the default CMA-ES with the advantages of separable CMA-ES without inheriting its drawbacks. Technically, we introduce a diagonal matrix D that expresses coordinate-wise variances of the sampling distribution in DCD form. The diagonal matrix can learn a rescaling of the problem in the coordinates within linear number of function evaluations. Diagonal decoding can also exploit separability of the problem, but, crucially, does not compromise the performance on non-separable problems. The latter is accomplished by modulating the learning rate for the diagonal matrix based on the condition number of the underlying correlation matrix. dd-CMA-ES not only combines the advantages of default and separable CMA-ES, but may achieve overadditive speedup: it improves the performance, and even the scaling, of the better of default and separable CMA-ES on classes of non-separable test functions that reflect, arguably, a landscape feature commonly observed in practice. The paper makes two further secondary contributions: we introduce two different approaches to guarantee positive definiteness of the covariance matrix with active CMA, which is valuable in particular with large population size; we revise the default parameter setting in CMA-ES, proposing accelerated settings in particular for large dimension. All our contributions can be viewed as independent improvements of CMA-ES, yet they are also complementary and can be seamlessly combined. In numerical experiments with dd-CMA-ES up to dimension 5120, we observe remarkable improvements over the original covariance matrix adaptation on functions with coordinate-wise ill-conditioning. The improvement is observed also for large population sizes up to about dimension squared.

Uncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework

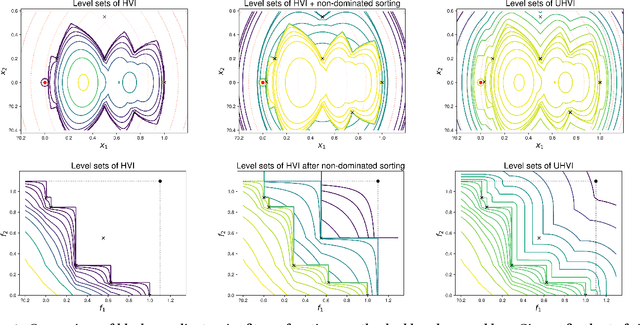
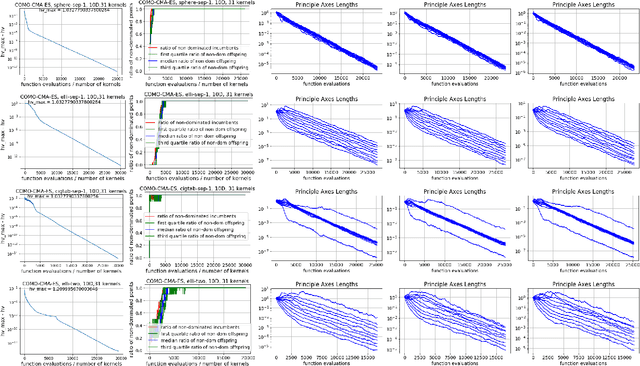
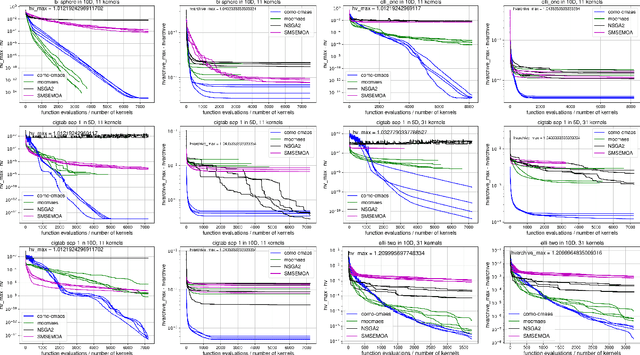
We present a framework to build a multiobjective algorithm from single-objective ones. This framework addresses the $p \times n$-dimensional problem of finding p solutions in an n-dimensional search space, maximizing an indicator by dynamic subspace optimization. Each single-objective algorithm optimizes the indicator function given $p - 1$ fixed solutions. Crucially, dominated solutions minimize their distance to the empirical Pareto front defined by these $p - 1$ solutions. We instantiate the framework with CMA-ES as single-objective optimizer. The new algorithm, COMO-CMA-ES, is empirically shown to converge linearly on bi-objective convex-quadratic problems and is compared to MO-CMA-ES, NSGA-II and SMS-EMOA.

COCO: The Large Scale Black-Box Optimization Benchmarking Test Suite

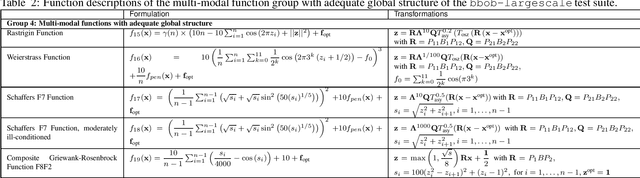
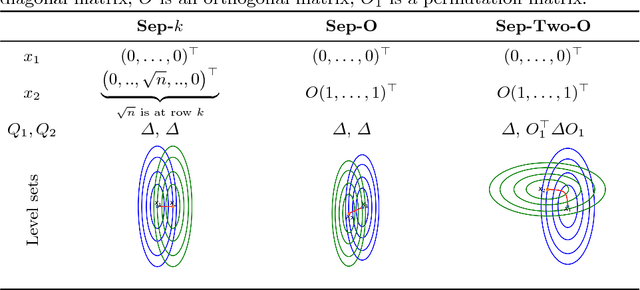
The bbob-largescale test suite, containing 24 single-objective functions in continuous domain, extends the well-known single-objective noiseless bbob test suite, which has been used since 2009 in the BBOB workshop series, to large dimension. The core idea is to make the rotational transformations R, Q in search space that appear in the bbob test suite computationally cheaper while retaining some desired properties. This documentation presents an approach that replaces a full rotational transformation with a combination of a block-diagonal matrix and two permutation matrices in order to construct test functions whose computational and memory costs scale linearly in the dimension of the problem.

On Bi-Objective convex-quadratic problems

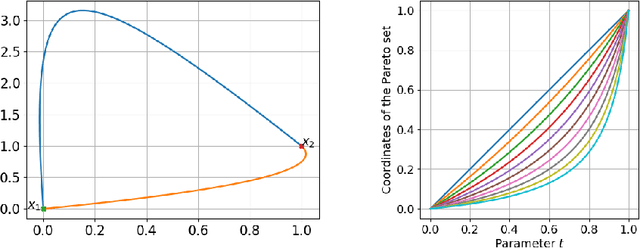
In this paper we analyze theoretical properties of bi-objective convex-quadratic problems. We give a complete description of their Pareto set and prove the convexity of their Pareto front. We show that the Pareto set is a line segment when both Hessian matrices are proportional. We then propose a novel set of convex-quadratic test problems, describe their theoretical properties and the algorithm abilities required by those test problems. This includes in particular testing the sensitivity with respect to separability, ill-conditioned problems, rotational invariance, and whether the Pareto set is aligned with the coordinate axis.

COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting

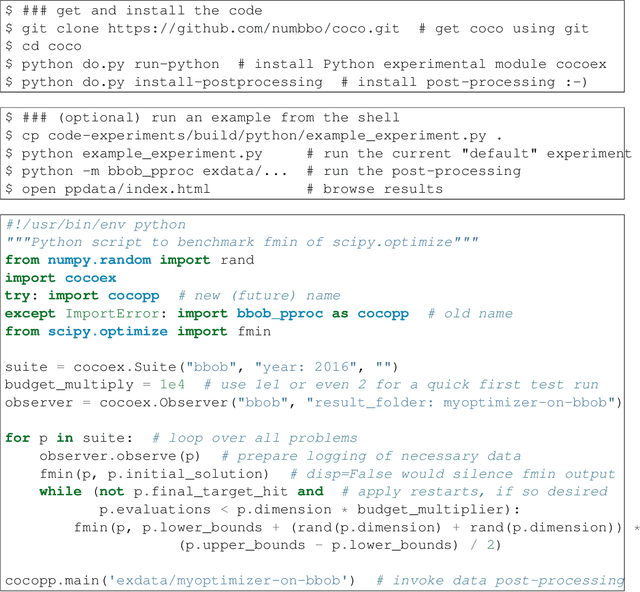
COCO is a platform for Comparing Continuous Optimizers in a black-box setting. It aims at automatizing the tedious and repetitive task of benchmarking numerical optimization algorithms to the greatest possible extent. We present the rationals behind the development of the platform as a general proposition for a guideline towards better benchmarking. We detail underlying fundamental concepts of COCO such as its definition of a problem, the idea of instances, the relevance of target values, and runtime as central performance measure. Finally, we give a quick overview of the basic code structure and the available test suites.

COCO: The Bi-objective Black Box Optimization Benchmarking Test Suite

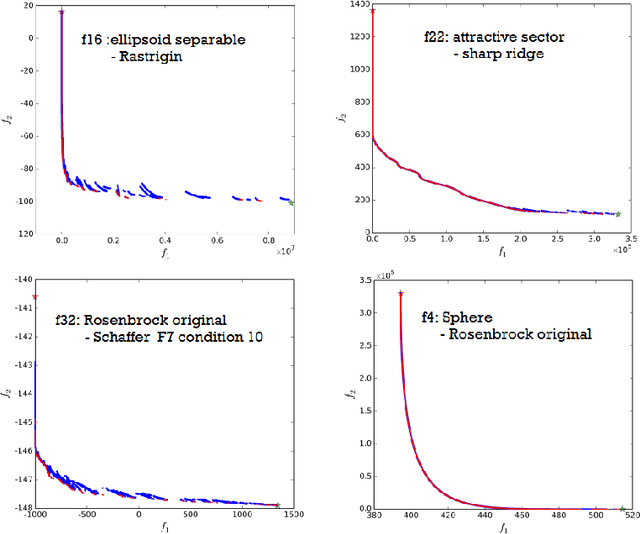
The bbob-biobj test suite contains 55 bi-objective functions in continuous domain which are derived from combining functions of the well-known single-objective noiseless bbob test suite. Besides giving the actual function definitions and presenting their (known) properties, this documentation also aims at giving the rationale behind our approach in terms of function groups, instances, and potential objective space normalization.

COCO: The Experimental Procedure

We present a budget-free experimental setup and procedure for benchmarking numericaloptimization algorithms in a black-box scenario. This procedure can be applied with the COCO benchmarking platform. We describe initialization of and input to the algorithm and touch upon therelevance of termination and restarts.

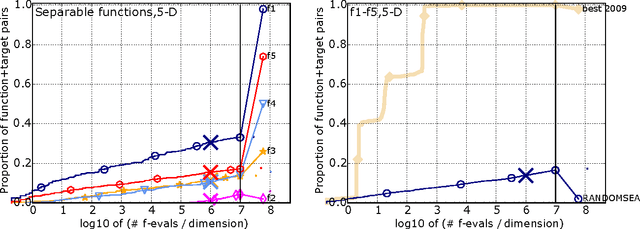
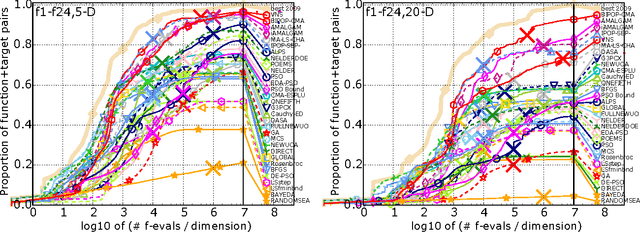
COCO: Performance Assessment

We present an any-time performance assessment for benchmarking numerical optimization algorithms in a black-box scenario, applied within the COCO benchmarking platform. The performance assessment is based on runtimes measured in number of objective function evaluations to reach one or several quality indicator target values. We argue that runtime is the only available measure with a generic, meaningful, and quantitative interpretation. We discuss the choice of the target values, runlength-based targets, and the aggregation of results by using simulated restarts, averages, and empirical distribution functions.

Biobjective Performance Assessment with the COCO Platform

This document details the rationales behind assessing the performance of numerical black-box optimizers on multi-objective problems within the COCO platform and in particular on the biobjective test suite bbob-biobj. The evaluation is based on a hypervolume of all non-dominated solutions in the archive of candidate solutions and measures the runtime until the hypervolume value succeeds prescribed target values.

The CMA Evolution Strategy: A Tutorial

This tutorial introduces the CMA Evolution Strategy (ES), where CMA stands for Covariance Matrix Adaptation. The CMA-ES is a stochastic, or randomized, method for real-parameter (continuous domain) optimization of non-linear, non-convex functions. We try to motivate and derive the algorithm from intuitive concepts and from requirements of non-linear, non-convex search in continuous domain.