Where the Really Hard Quadratic Assignment Problems Are: the QAP-SAT instances

The Quadratic Assignment Problem (QAP) is one of the major domains in the field of evolutionary computation, and more widely in combinatorial optimization. This paper studies the phase transition of the QAP, which can be described as a dramatic change in the problem's computational complexity and satisfiability, within a narrow range of the problem parameters. To approach this phenomenon, we introduce a new QAP-SAT design of the initial problem based on submodularity to capture its difficulty with new features. This decomposition is studied experimentally using branch-and-bound and tabu search solvers. A phase transition parameter is then proposed. The critical parameter of phase transition satisfaction and that of the solving effort are shown to be highly correlated for tabu search, thus allowing the prediction of difficult instances.

A Fitness Landscape View on the Tuning of an Asynchronous Master-Worker EA for Nuclear Reactor Design

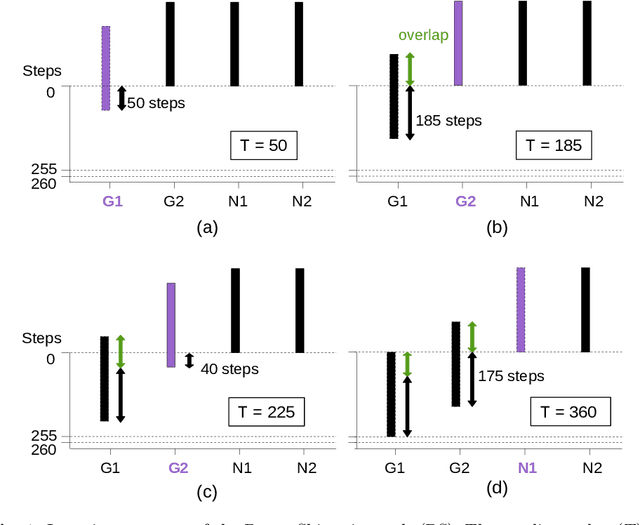
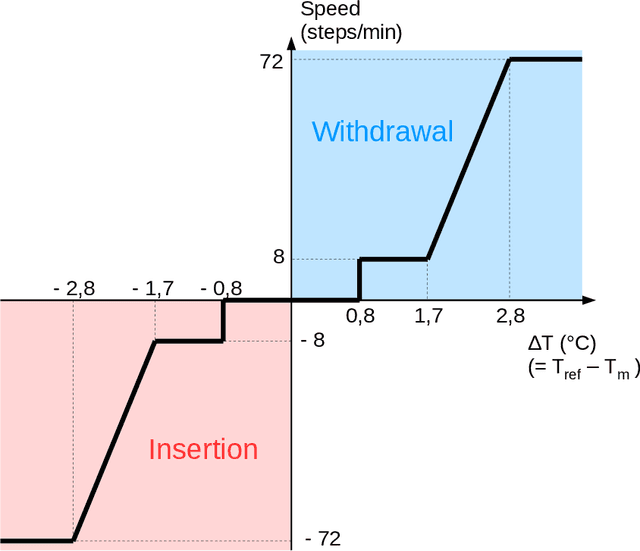
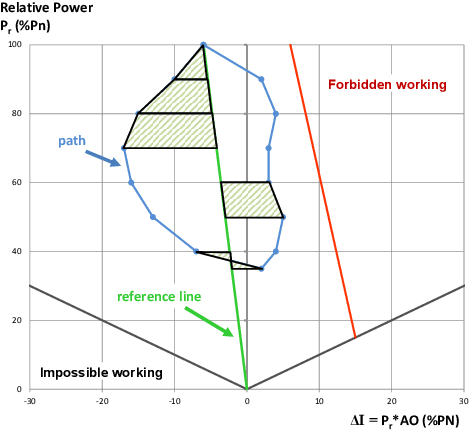
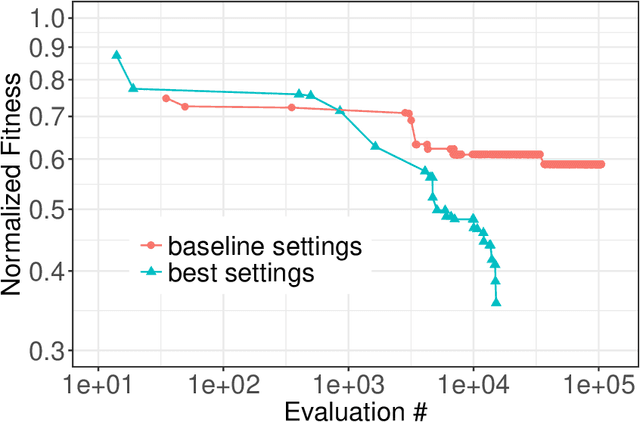
In the context of the introduction of intermittent renewable energies, we propose to optimize the main variables of the control rods of a nuclear power plant to improve its capability to load-follow. The design problem is a black-box combinatorial optimization problem with expensive evaluation based on a multi-physics simulator. Therefore, we use a parallel asynchronous master-worker Evolutionary Algorithm scaling up to thousand computing units. One main issue is the tuning of the algorithm parameters. A fitness landscape analysis is conducted on this expensive real-world problem to show that it would be possible to tune the mutation parameters according to the low-cost estimation of the fitness landscape features.

Paradiseo: From a Modular Framework for Evolutionary Computation to the Automated Design of Metaheuristics ---22 Years of Paradiseo---

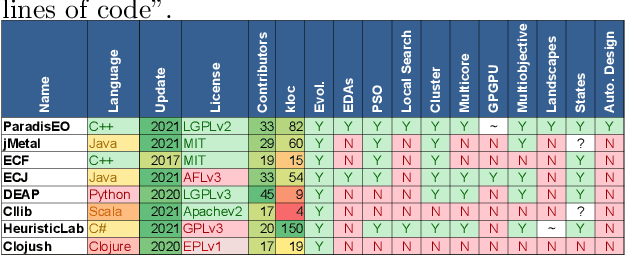
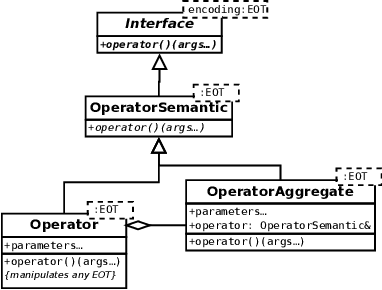
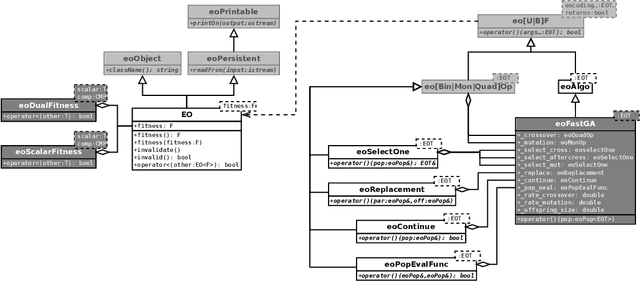
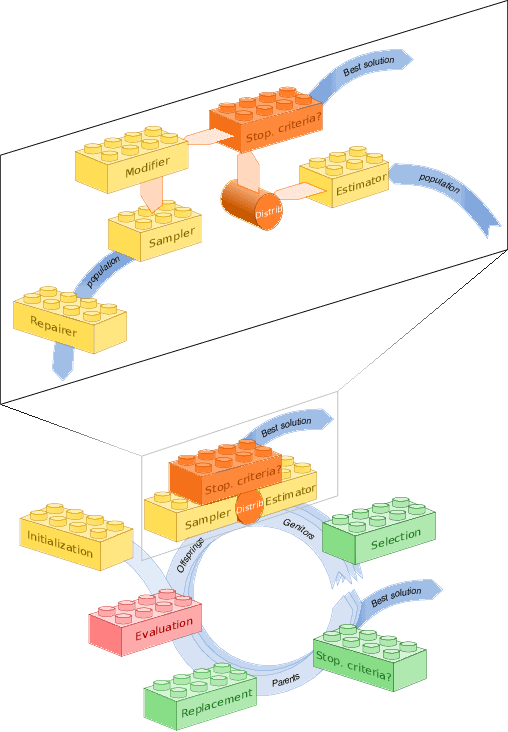
The success of metaheuristic optimization methods has led to the development of a large variety of algorithm paradigms. However, no algorithm clearly dominates all its competitors on all problems. Instead, the underlying variety of landscapes of optimization problems calls for a variety of algorithms to solve them efficiently. It is thus of prior importance to have access to mature and flexible software frameworks which allow for an efficient exploration of the algorithm design space. Such frameworks should be flexible enough to accommodate any kind of metaheuristics, and open enough to connect with higher-level optimization, monitoring and evaluation softwares. This article summarizes the features of the ParadisEO framework, a comprehensive C++ free software which targets the development of modular metaheuristics. ParadisEO provides a highly modular architecture, a large set of components, speed of execution and automated algorithm design features, which are key to modern approaches to metaheuristics development.

An Analysis on Selection for High-Resolution Approximations in Many-Objective Optimization

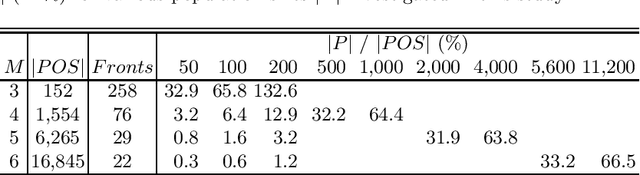
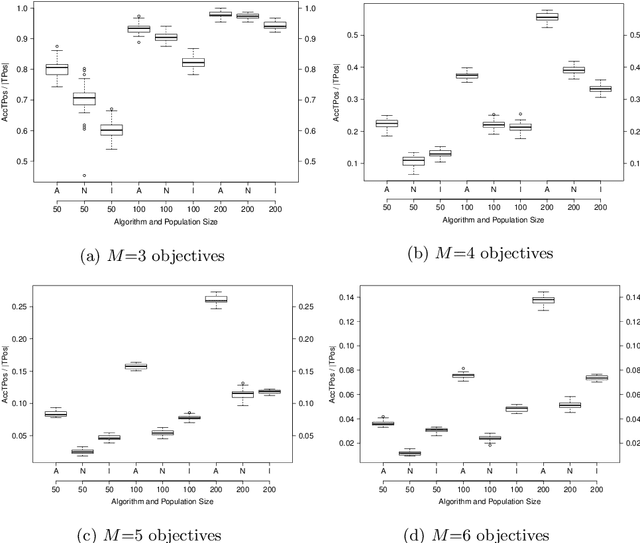
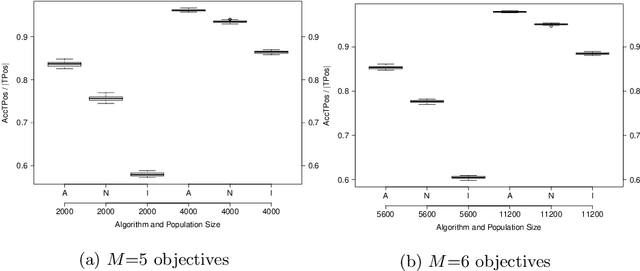
This work studies the behavior of three elitist multi- and many-objective evolutionary algorithms generating a high-resolution approximation of the Pareto optimal set. Several search-assessment indicators are defined to trace the dynamics of survival selection and measure the ability to simultaneously keep optimal solutions and discover new ones under different population sizes, set as a fraction of the size of the Pareto optimal set.

On the Impact of Multiobjective Scalarizing Functions

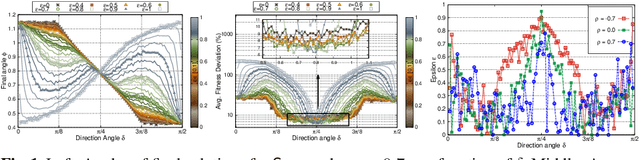
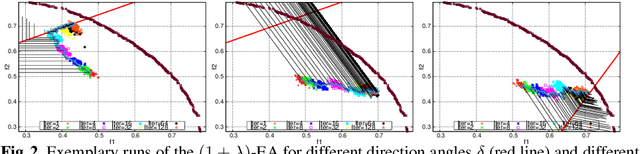
Recently, there has been a renewed interest in decomposition-based approaches for evolutionary multiobjective optimization. However, the impact of the choice of the underlying scalarizing function(s) is still far from being well understood. In this paper, we investigate the behavior of different scalarizing functions and their parameters. We thereby abstract firstly from any specific algorithm and only consider the difficulty of the single scalarized problems in terms of the search ability of a (1+lambda)-EA on biobjective NK-landscapes. Secondly, combining the outcomes of independent single-objective runs allows for more general statements on set-based performance measures. Finally, we investigate the correlation between the opening angle of the scalarizing function's underlying contour lines and the position of the final solution in the objective space. Our analysis is of fundamental nature and sheds more light on the key characteristics of multiobjective scalarizing functions.

Local Optimal Sets and Bounded Archiving on Multi-objective NK-Landscapes with Correlated Objectives

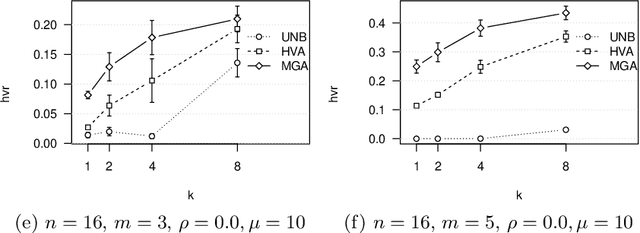
The properties of local optimal solutions in multi-objective combinatorial optimization problems are crucial for the effectiveness of local search algorithms, particularly when these algorithms are based on Pareto dominance. Such local search algorithms typically return a set of mutually nondominated Pareto local optimal (PLO) solutions, that is, a PLO-set. This paper investigates two aspects of PLO-sets by means of experiments with Pareto local search (PLS). First, we examine the impact of several problem characteristics on the properties of PLO-sets for multi-objective NK-landscapes with correlated objectives. In particular, we report that either increasing the number of objectives or decreasing the correlation between objectives leads to an exponential increment on the size of PLO-sets, whereas the variable correlation has only a minor effect. Second, we study the running time and the quality reached when using bounding archiving methods to limit the size of the archive handled by PLS, and thus, the maximum size of the PLO-set found. We argue that there is a clear relationship between the running time of PLS and the difficulty of a problem instance.

Local Optima Networks: A New Model of Combinatorial Fitness Landscapes

This chapter overviews a recently introduced network-based model of combinatorial landscapes: Local Optima Networks (LON). The model compresses the information given by the whole search space into a smaller mathematical object that is a graph having as vertices the local optima and as edges the possible weighted transitions between them. Two definitions of edges have been proposed: basin-transition and escape-edges, which capture relevant topological features of the underlying search spaces. This network model brings a new set of metrics to characterize the structure of combinatorial landscapes, those associated with the science of complex networks. These metrics are described, and results are presented of local optima network extraction and analysis for two selected combinatorial landscapes: NK landscapes and the quadratic assignment problem. Network features are found to correlate with and even predict the performance of heuristic search algorithms operating on these problems.

Local Optima Networks, Landscape Autocorrelation and Heuristic Search Performance

Recent developments in fitness landscape analysis include the study of Local Optima Networks (LON) and applications of the Elementary Landscapes theory. This paper represents a first step at combining these two tools to explore their ability to forecast the performance of search algorithms. We base our analysis on the Quadratic Assignment Problem (QAP) and conduct a large statistical study over 600 generated instances of different types. Our results reveal interesting links between the network measures, the autocorrelation measures and the performance of heuristic search algorithms.

Local optima networks and the performance of iterated local search

Local Optima Networks (LONs) have been recently proposed as an alternative model of combinatorial fitness landscapes. The model compresses the information given by the whole search space into a smaller mathematical object that is the graph having as vertices the local optima and as edges the possible weighted transitions between them. A new set of metrics can be derived from this model that capture the distribution and connectivity of the local optima in the underlying configuration space. This paper departs from the descriptive analysis of local optima networks, and actively studies the correlation between network features and the performance of a local search heuristic. The NK family of landscapes and the Iterated Local Search metaheuristic are considered. With a statistically-sound approach based on multiple linear regression, it is shown that some LONs' features strongly influence and can even partly predict the performance of a heuristic search algorithm. This study validates the expressive power of LONs as a model of combinatorial fitness landscapes.

Clustering of Local Optima in Combinatorial Fitness Landscapes

Using the recently proposed model of combinatorial landscapes: local optima networks, we study the distribution of local optima in two classes of instances of the quadratic assignment problem. Our results indicate that the two problem instance classes give rise to very different configuration spaces. For the so-called real-like class, the optima networks possess a clear modular structure, while the networks belonging to the class of random uniform instances are less well partitionable into clusters. We briefly discuss the consequences of the findings for heuristically searching the corresponding problem spaces.