Arnaud Liefooghe
Univ. Lille, CNRS, Inria, Centrale Lille, UMR 9189 CRIStAL, Lille, France
Applying Ising Machines to Multi-objective QUBOs
May 19, 2023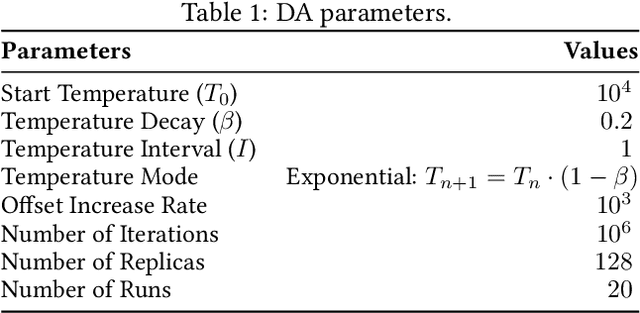
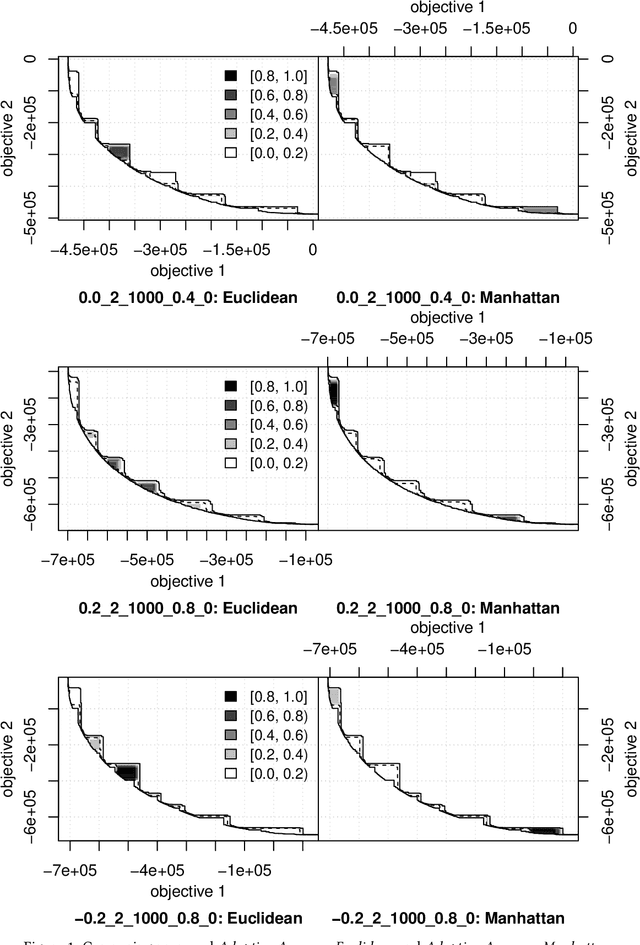
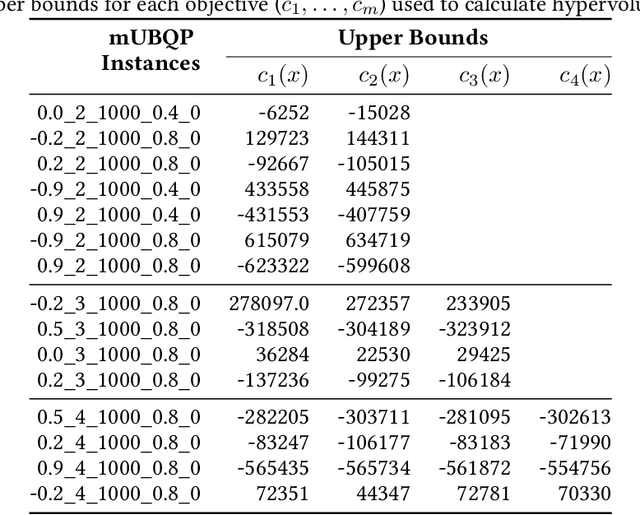
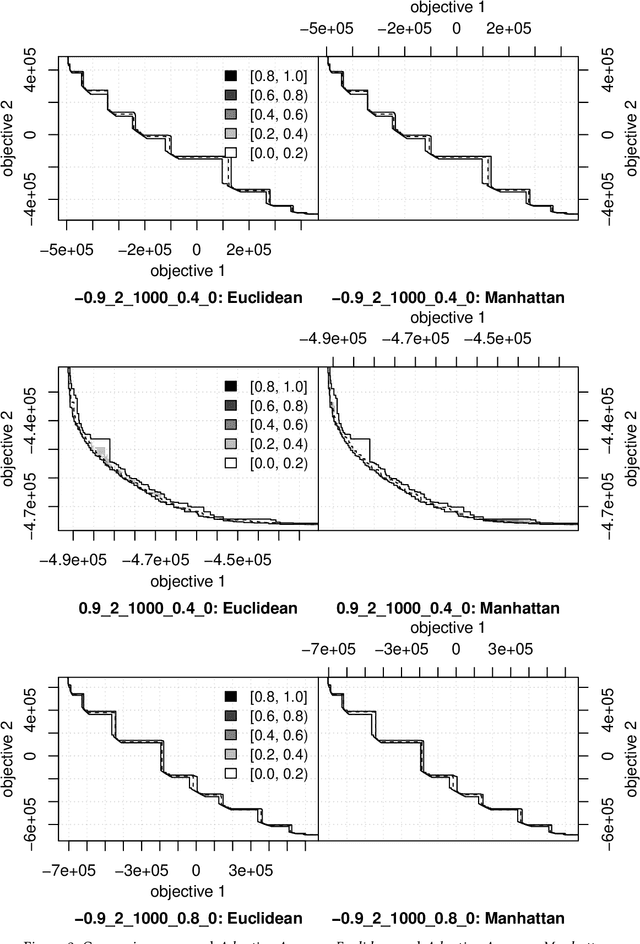
Abstract:Multi-objective optimisation problems involve finding solutions with varying trade-offs between multiple and often conflicting objectives. Ising machines are physical devices that aim to find the absolute or approximate ground states of an Ising model. To apply Ising machines to multi-objective problems, a weighted sum objective function is used to convert multi-objective into single-objective problems. However, deriving scalarisation weights that archives evenly distributed solutions across the Pareto front is not trivial. Previous work has shown that adaptive weights based on dichotomic search, and one based on averages of previously explored weights can explore the Pareto front quicker than uniformly generated weights. However, these adaptive methods have only been applied to bi-objective problems in the past. In this work, we extend the adaptive method based on averages in two ways: (i)~we extend the adaptive method of deriving scalarisation weights for problems with two or more objectives, and (ii)~we use an alternative measure of distance to improve performance. We compare the proposed method with existing ones and show that it leads to the best performance on multi-objective Unconstrained Binary Quadratic Programming (mUBQP) instances with 3 and 4 objectives and that it is competitive with the best one for instances with 2 objectives.
What if we Increase the Number of Objectives? Theoretical and Empirical Implications for Many-objective Optimization
Jun 06, 2021
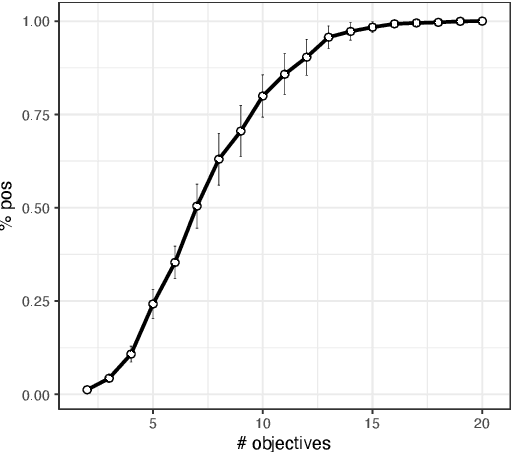
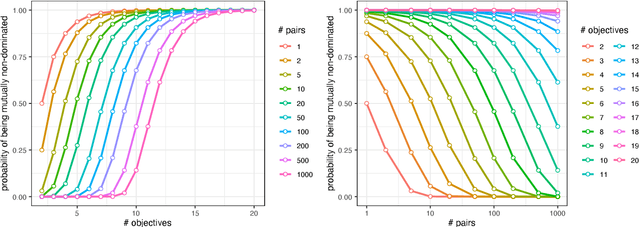
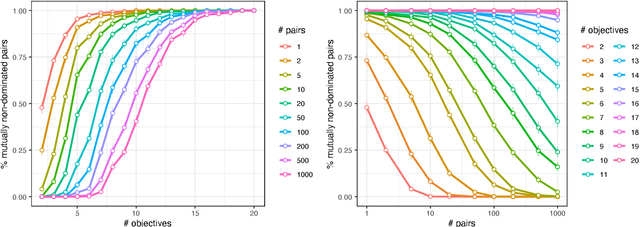
Abstract:The difficulty of solving a multi-objective optimization problem is impacted by the number of objectives to be optimized. The presence of many objectives typically introduces a number of challenges that affect the choice/design of optimization algorithms. This paper investigates the drivers of these challenges from two angles: (i) the influence of the number of objectives on problem characteristics and (ii) the practical behavior of commonly used procedures and algorithms for coping with many objectives. In addition to reviewing various drivers, the paper makes theoretical contributions by quantifying some drivers and/or verifying these drivers empirically by carrying out experiments on multi-objective NK landscapes and other typical benchmarks. We then make use of our theoretical and empirical findings to derive practical recommendations to support algorithm design. Finally, we discuss remaining theoretical gaps and opportunities for future research in the area of multi- and many-objective optimization.
Paradiseo: From a Modular Framework for Evolutionary Computation to the Automated Design of Metaheuristics ---22 Years of Paradiseo---
May 02, 2021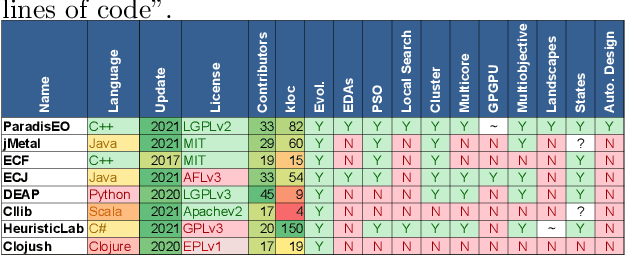
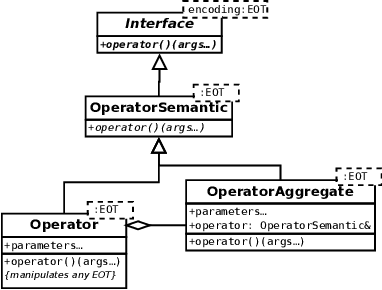
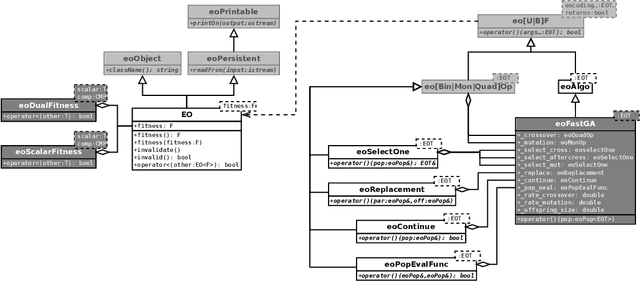
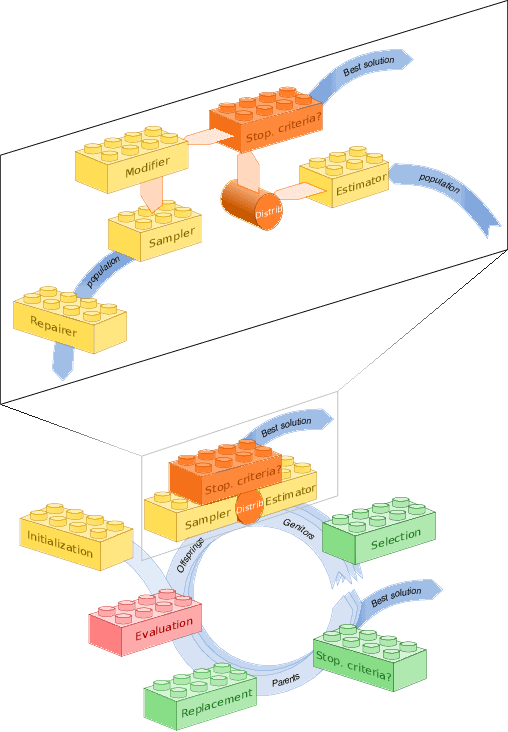
Abstract:The success of metaheuristic optimization methods has led to the development of a large variety of algorithm paradigms. However, no algorithm clearly dominates all its competitors on all problems. Instead, the underlying variety of landscapes of optimization problems calls for a variety of algorithms to solve them efficiently. It is thus of prior importance to have access to mature and flexible software frameworks which allow for an efficient exploration of the algorithm design space. Such frameworks should be flexible enough to accommodate any kind of metaheuristics, and open enough to connect with higher-level optimization, monitoring and evaluation softwares. This article summarizes the features of the ParadisEO framework, a comprehensive C++ free software which targets the development of modular metaheuristics. ParadisEO provides a highly modular architecture, a large set of components, speed of execution and automated algorithm design features, which are key to modern approaches to metaheuristics development.
On the Combined Impact of Population Size and Sub-problem Selection in MOEA/D
Apr 15, 2020
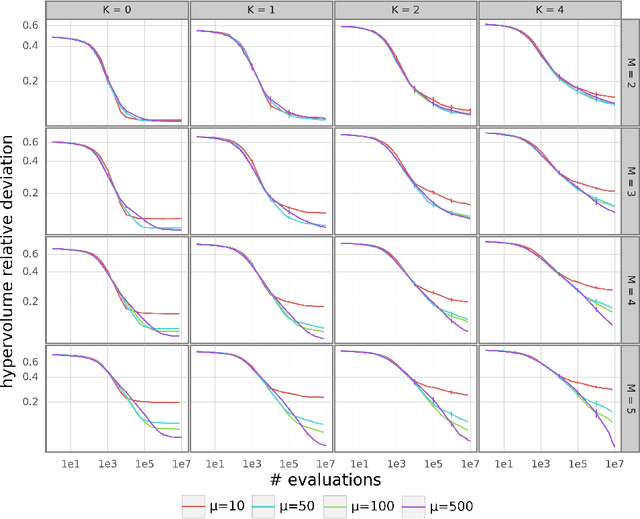
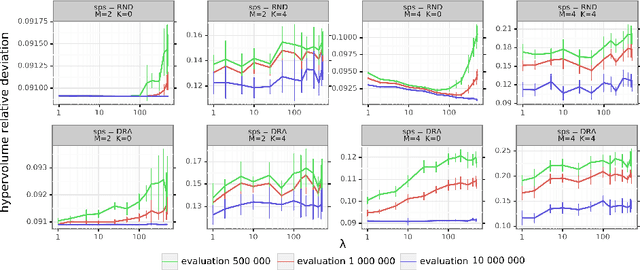
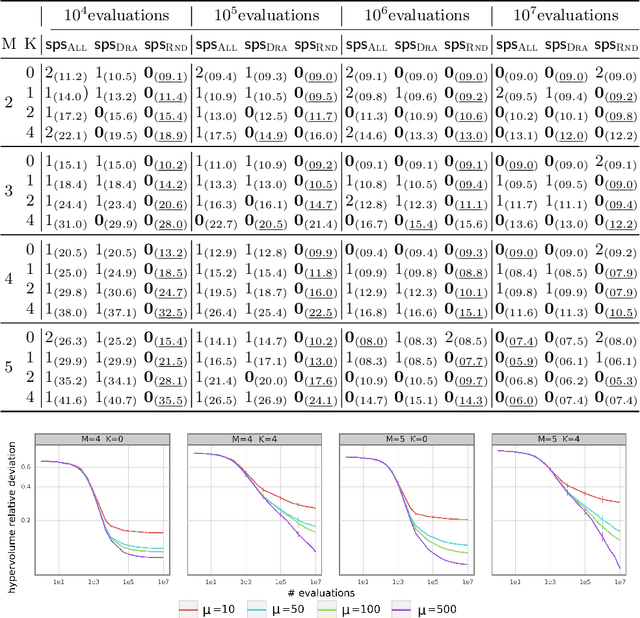
Abstract:This paper intends to understand and to improve the working principle of decomposition-based multi-objective evolutionary algorithms. We review the design of the well-established Moea/d framework to support the smooth integration of different strategies for sub-problem selection, while emphasizing the role of the population size and of the number of offspring created at each generation. By conducting a comprehensive empirical analysis on a wide range of multi-and many-objective combinatorial NK landscapes, we provide new insights into the combined effect of those parameters on the anytime performance of the underlying search process. In particular, we show that even a simple random strategy selecting sub-problems at random outperforms existing sophisticated strategies. We also study the sensitivity of such strategies with respect to the ruggedness and the objective space dimension of the target problem.
Surrogate Assisted Evolutionary Algorithm for Medium Scale Expensive Multi-Objective Optimisation Problems
Feb 08, 2020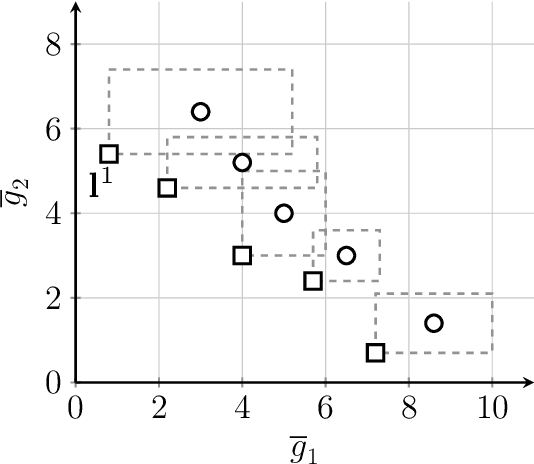
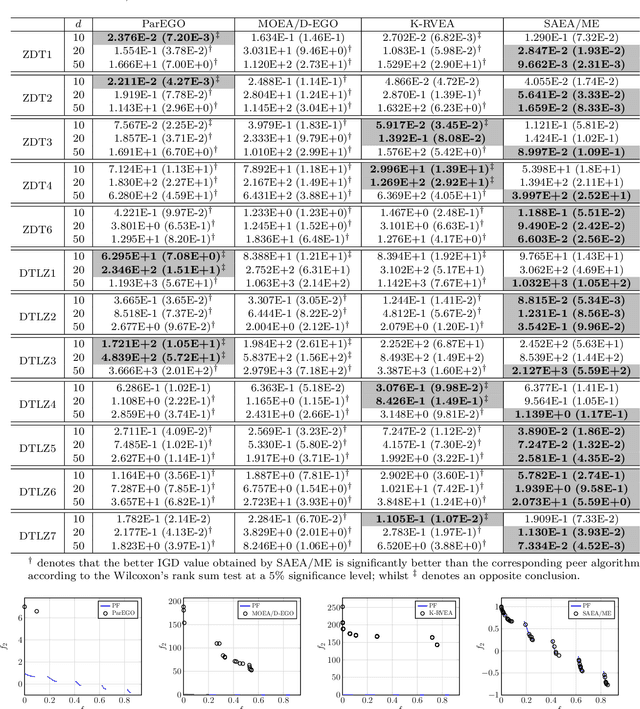

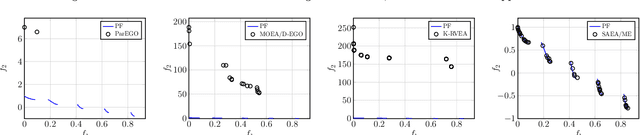
Abstract:Building a surrogate model of an objective function has shown to be effective to assist evolutionary algorithms (EAs) to solve real-world complex optimisation problems which involve either computationally expensive numerical simulations or costly physical experiments. However, their effectiveness mostly focuses on small-scale problems with less than 10 decision variables. The scalability of surrogate assisted EAs (SAEAs) have not been well studied yet. In this paper, we propose a Gaussian process surrogate model assisted EA for medium-scale expensive multi-objective optimisation problems with up to 50 decision variables. There are three distinctive features of our proposed SAEA. First, instead of using all decision variables in surrogate model building, we only use those correlated ones to build the surrogate model for each objective function. Second, rather than directly optimising the surrogate objective functions, the original multi-objective optimisation problem is transformed to a new one based on the surrogate models. Last but not the least, a subset selection method is developed to choose a couple of promising candidate solutions for actual objective function evaluations thus to update the training dataset. The effectiveness of our proposed algorithm is validated on benchmark problems with 10, 20, 50 variables, comparing with three state-of-the-art SAEAs.
An Analysis on Selection for High-Resolution Approximations in Many-Objective Optimization
Sep 26, 2014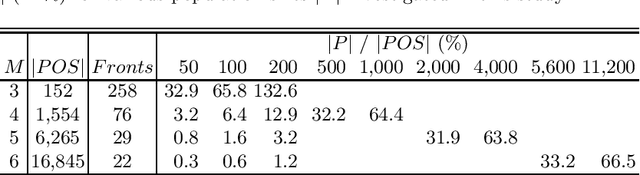
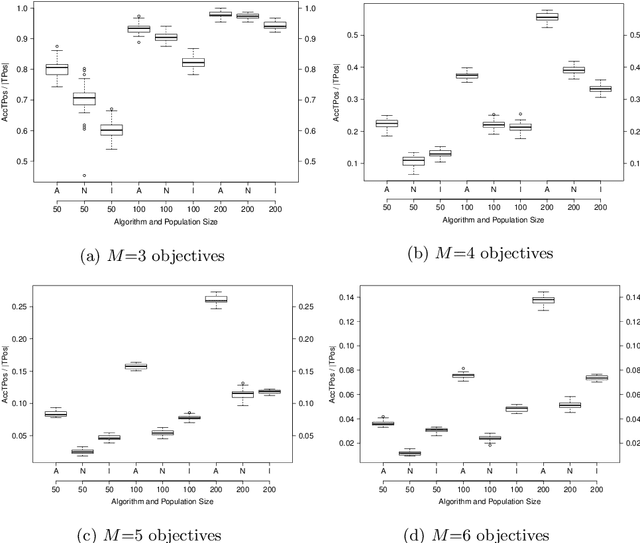

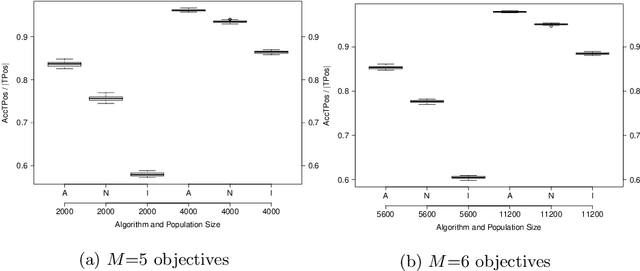
Abstract:This work studies the behavior of three elitist multi- and many-objective evolutionary algorithms generating a high-resolution approximation of the Pareto optimal set. Several search-assessment indicators are defined to trace the dynamics of survival selection and measure the ability to simultaneously keep optimal solutions and discover new ones under different population sizes, set as a fraction of the size of the Pareto optimal set.
On the Impact of Multiobjective Scalarizing Functions
Sep 19, 2014
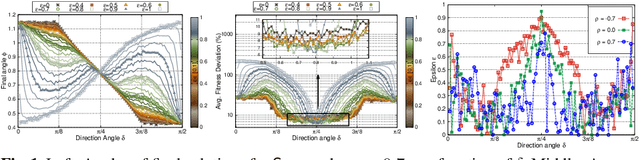

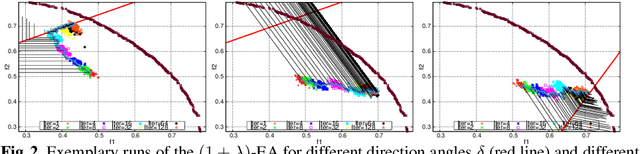
Abstract:Recently, there has been a renewed interest in decomposition-based approaches for evolutionary multiobjective optimization. However, the impact of the choice of the underlying scalarizing function(s) is still far from being well understood. In this paper, we investigate the behavior of different scalarizing functions and their parameters. We thereby abstract firstly from any specific algorithm and only consider the difficulty of the single scalarized problems in terms of the search ability of a (1+lambda)-EA on biobjective NK-landscapes. Secondly, combining the outcomes of independent single-objective runs allows for more general statements on set-based performance measures. Finally, we investigate the correlation between the opening angle of the scalarizing function's underlying contour lines and the position of the final solution in the objective space. Our analysis is of fundamental nature and sheds more light on the key characteristics of multiobjective scalarizing functions.
Local Optimal Sets and Bounded Archiving on Multi-objective NK-Landscapes with Correlated Objectives
Sep 19, 2014
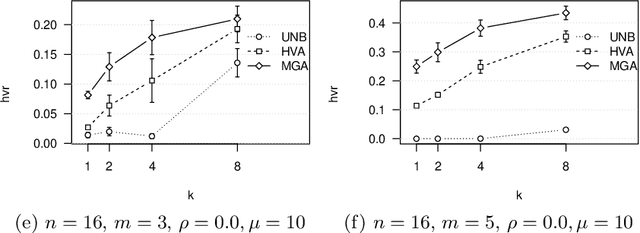

Abstract:The properties of local optimal solutions in multi-objective combinatorial optimization problems are crucial for the effectiveness of local search algorithms, particularly when these algorithms are based on Pareto dominance. Such local search algorithms typically return a set of mutually nondominated Pareto local optimal (PLO) solutions, that is, a PLO-set. This paper investigates two aspects of PLO-sets by means of experiments with Pareto local search (PLS). First, we examine the impact of several problem characteristics on the properties of PLO-sets for multi-objective NK-landscapes with correlated objectives. In particular, we report that either increasing the number of objectives or decreasing the correlation between objectives leads to an exponential increment on the size of PLO-sets, whereas the variable correlation has only a minor effect. Second, we study the running time and the quality reached when using bounding archiving methods to limit the size of the archive handled by PLS, and thus, the maximum size of the PLO-set found. We argue that there is a clear relationship between the running time of PLS and the difficulty of a problem instance.
Analyzing the Effect of Objective Correlation on the Efficient Set of MNK-Landscapes
Jul 19, 2012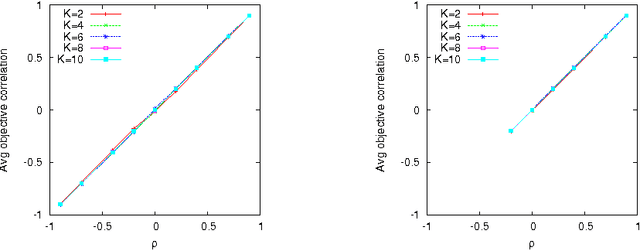
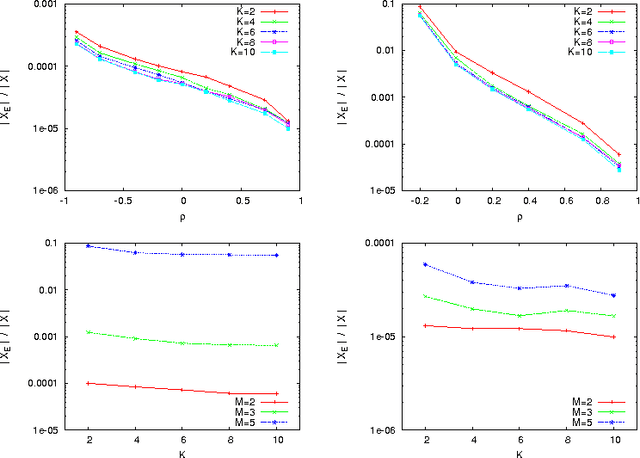
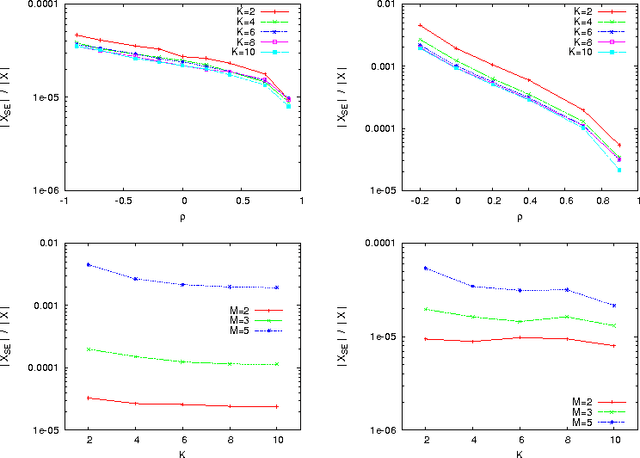
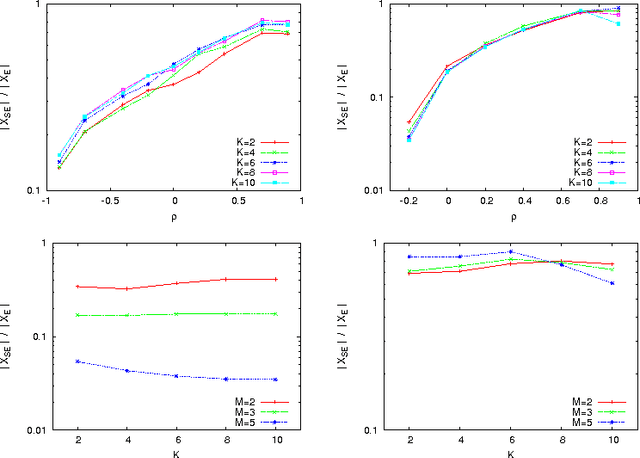
Abstract:In multiobjective combinatorial optimization, there exists two main classes of metaheuristics, based either on multiple aggregations, or on a dominance relation. As in the single objective case, the structure of the search space can explain the difficulty for multiobjective metaheuristics, and guide the design of such methods. In this work we analyze the properties of multiobjective combinatorial search spaces. In particular, we focus on the features related the efficient set, and we pay a particular attention to the correlation between objectives. Few benchmark takes such objective correlation into account. Here, we define a general method to design multiobjective problems with correlation. As an example, we extend the well-known multiobjective NK-landscapes. By measuring different properties of the search space, we show the importance of considering the objective correlation on the design of metaheuristics.
On the Neutrality of Flowshop Scheduling Fitness Landscapes
Jul 19, 2012
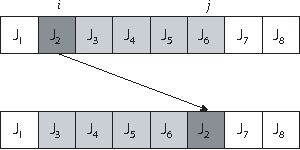
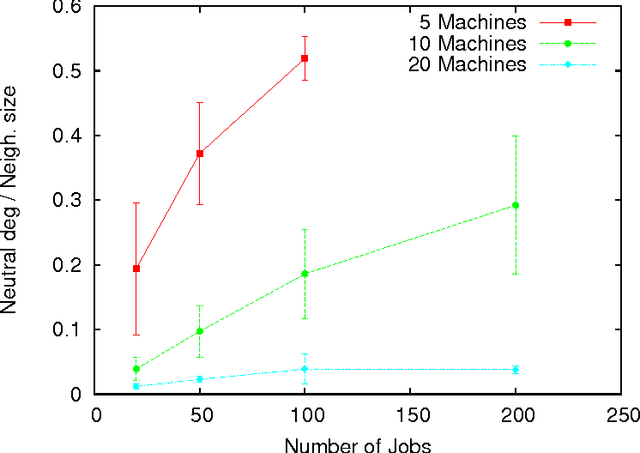
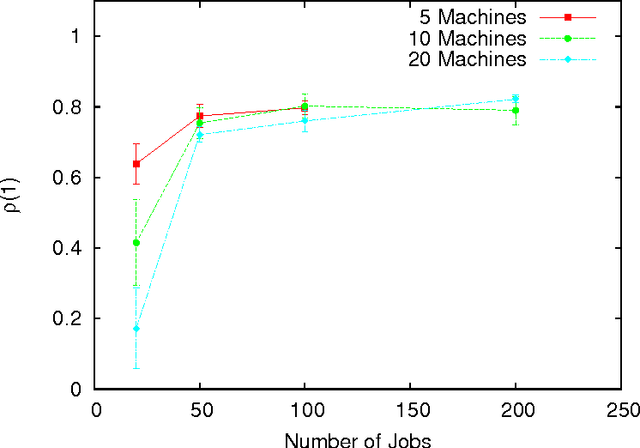
Abstract:Solving efficiently complex problems using metaheuristics, and in particular local searches, requires incorporating knowledge about the problem to solve. In this paper, the permutation flowshop problem is studied. It is well known that in such problems, several solutions may have the same fitness value. As this neutrality property is an important one, it should be taken into account during the design of optimization methods. Then in the context of the permutation flowshop, a deep landscape analysis focused on the neutrality property is driven and propositions on the way to use this neutrality to guide efficiently the search are given.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge