A Study on the Impact of Fault localization Granularity for Repository-Scale Code Repair Tasks

Automatic program repair can be a challenging task, especially when resolving complex issues at a repository-level, which often involves issue reproduction, fault localization, code repair, testing and validation. Issues of this scale can be commonly found in popular GitHub repositories or datasets that are derived from them. Some repository-level approaches separate localization and repair into distinct phases. Where this is the case, the fault localization approaches vary in terms of the granularity of localization. Where the impact of granularity is explored to some degree for smaller datasets, not all isolate this issue from the separate question of localization accuracy by testing code repair under the assumption of perfect fault localization. To the best of the authors' knowledge, no repository-scale studies have explicitly investigated granularity under this assumption, nor conducted a systematic empirical comparison of granularity levels in isolation. We propose a framework for performing such tests by modifying the localization phase of the Agentless framework to retrieve ground-truth localization data and include this as context in the prompt fed to the repair phase. We show that under this configuration and as a generalization over the SWE-Bench-Mini dataset, function-level granularity yields the highest repair rate against line-level and file-level. However, a deeper dive suggests that the ideal granularity may in fact be task dependent. This study is not intended to improve on the state-of-the-art, nor do we intend for results to be compared against any complete agentic frameworks. Rather, we present a proof of concept for investigating how fault localization may impact automatic code repair in repository-scale scenarios. We present preliminary findings to this end and encourage further research into this relationship between the two phases.

Fast instance-specific algorithm configuration with graph neural network

Combinatorial optimization (CO) problems are pivotal across various industrial applications, where the speed of solving these problems is crucial. Improving the performance of CO solvers across diverse input instances requires fine-tuning solver parameters for each instance. However, this tuning process is time-consuming, and the time required increases with the number of instances. To address this, a method called instance-specific algorithm configuration (ISAC) has been devised. This approach involves two main steps: training and execution. During the training step, features are extracted from various instances and then grouped into clusters. For each cluster, parameters are fine-tuned. This cluster-specific tuning process results in a set of generalized parameters for instances belonging to each class. In the execution step, features are extracted from an unknown instance to determine its cluster, and the corresponding pre-tuned parameters are applied. Generally, the running time of a solver is evaluated by the time to solution ($TTS$). However, methods like ISAC require preprocessing. Therefore, the total execution time is $T_{tot}=TTS+T_{tune}$, where $T_{tune}$ represents the tuning time. While the goal is to minimize $T_{tot}$, it is important to note that extracting features in the ISAC method requires a certain amount of computational time. The extracting features include summary statistics of the solver execution logs, which takes several 10 seconds. This research presents a method to significantly reduce the time of the ISAC execution step by streamlining feature extraction and class determination with a graph neural network. Experimental results show that $T_{tune}$ in the execution step, which take several 10 seconds in the original ISAC manner, could be reduced to sub-seconds.

Applying Ising Machines to Multi-objective QUBOs

Multi-objective optimisation problems involve finding solutions with varying trade-offs between multiple and often conflicting objectives. Ising machines are physical devices that aim to find the absolute or approximate ground states of an Ising model. To apply Ising machines to multi-objective problems, a weighted sum objective function is used to convert multi-objective into single-objective problems. However, deriving scalarisation weights that archives evenly distributed solutions across the Pareto front is not trivial. Previous work has shown that adaptive weights based on dichotomic search, and one based on averages of previously explored weights can explore the Pareto front quicker than uniformly generated weights. However, these adaptive methods have only been applied to bi-objective problems in the past. In this work, we extend the adaptive method based on averages in two ways: (i)~we extend the adaptive method of deriving scalarisation weights for problems with two or more objectives, and (ii)~we use an alternative measure of distance to improve performance. We compare the proposed method with existing ones and show that it leads to the best performance on multi-objective Unconstrained Binary Quadratic Programming (mUBQP) instances with 3 and 4 objectives and that it is competitive with the best one for instances with 2 objectives.

Fast Hyperparameter Tuning for Ising Machines

In this paper, we propose a novel technique to accelerate Ising machines hyperparameter tuning. Firstly, we define Ising machine performance and explain the goal of hyperparameter tuning in regard to this performance definition. Secondly, we compare well-known hyperparameter tuning techniques, namely random sampling and Tree-structured Parzen Estimator (TPE) on different combinatorial optimization problems. Thirdly, we propose a new convergence acceleration method for TPE which we call "FastConvergence".It aims at limiting the number of required TPE trials to reach best performing hyperparameter values combination. We compare FastConvergence to previously mentioned well-known hyperparameter tuning techniques to show its effectiveness. For experiments, well-known Travel Salesman Problem (TSP) and Quadratic Assignment Problem (QAP) instances are used as input. The Ising machine used is Fujitsu's third generation Digital Annealer (DA). Results show, in most cases, FastConvergence can reach similar results to TPE alone within less than half the number of trials.

A Study of Scalarisation Techniques for Multi-Objective QUBO Solving

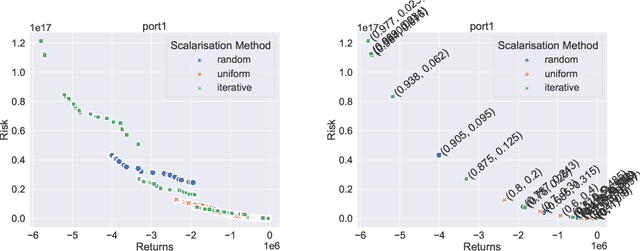
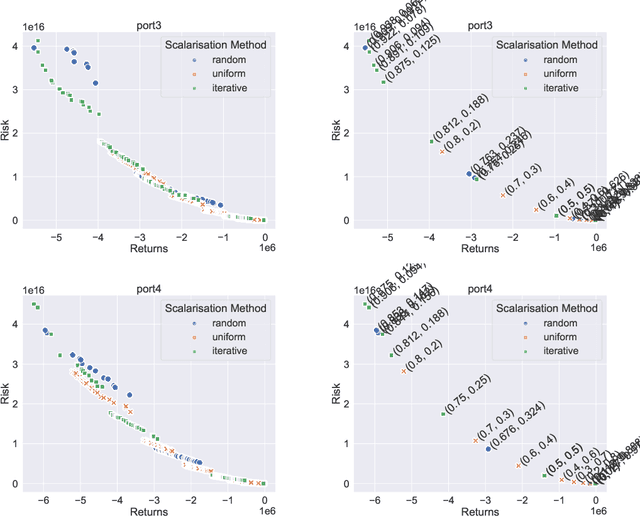
In recent years, there has been significant research interest in solving Quadratic Unconstrained Binary Optimisation (QUBO) problems. Physics-inspired optimisation algorithms have been proposed for deriving optimal or sub-optimal solutions to QUBOs. These methods are particularly attractive within the context of using specialised hardware, such as quantum computers, application specific CMOS and other high performance computing resources for solving optimisation problems. These solvers are then applied to QUBO formulations of combinatorial optimisation problems. Quantum and quantum-inspired optimisation algorithms have shown promising performance when applied to academic benchmarks as well as real-world problems. However, QUBO solvers are single objective solvers. To make them more efficient at solving problems with multiple objectives, a decision on how to convert such multi-objective problems to single-objective problems need to be made. In this study, we compare methods of deriving scalarisation weights when combining two objectives of the cardinality constrained mean-variance portfolio optimisation problem into one. We show significant performance improvement (measured in terms of hypervolume) when using a method that iteratively fills the largest space in the Pareto front compared to a n\"aive approach using uniformly generated weights.

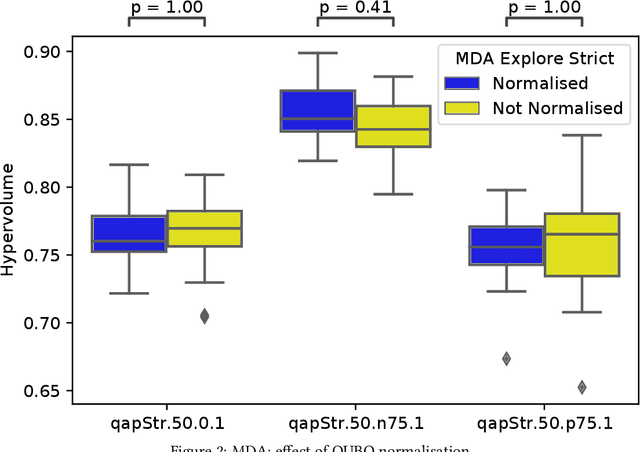
Multi-objective QUBO Solver: Bi-objective Quadratic Assignment

Quantum and quantum-inspired optimisation algorithms are designed to solve problems represented in binary, quadratic and unconstrained form. Combinatorial optimisation problems are therefore often formulated as Quadratic Unconstrained Binary Optimisation Problems (QUBO) to solve them with these algorithms. Moreover, these QUBO solvers are often implemented using specialised hardware to achieve enormous speedups, e.g. Fujitsu's Digital Annealer (DA) and D-Wave's Quantum Annealer. However, these are single-objective solvers, while many real-world problems feature multiple conflicting objectives. Thus, a common practice when using these QUBO solvers is to scalarise such multi-objective problems into a sequence of single-objective problems. Due to design trade-offs of these solvers, formulating each scalarisation may require more time than finding a local optimum. We present the first attempt to extend the algorithm supporting a commercial QUBO solver as a multi-objective solver that is not based on scalarisation. The proposed multi-objective DA algorithm is validated on the bi-objective Quadratic Assignment Problem. We observe that algorithm performance significantly depends on the archiving strategy adopted, and that combining DA with non-scalarisation methods to optimise multiple objectives outperforms the current scalarised version of the DA in terms of final solution quality.