Utilising a Quantum Hybrid Solver for Bi-objective Quadratic Assignment Problems

The intersection between quantum computing and optimisation has been an area of interest in recent years. There have been numerous studies exploring the application of quantum and quantum-hybrid solvers to various optimisation problems. This work explores scalarisation methods within the context of solving the bi-objective quadratic assignment problem using a quantum-hybrid solver. We show results that are consistent with previous research on a different Ising machine.

Applying Ising Machines to Multi-objective QUBOs

Multi-objective optimisation problems involve finding solutions with varying trade-offs between multiple and often conflicting objectives. Ising machines are physical devices that aim to find the absolute or approximate ground states of an Ising model. To apply Ising machines to multi-objective problems, a weighted sum objective function is used to convert multi-objective into single-objective problems. However, deriving scalarisation weights that archives evenly distributed solutions across the Pareto front is not trivial. Previous work has shown that adaptive weights based on dichotomic search, and one based on averages of previously explored weights can explore the Pareto front quicker than uniformly generated weights. However, these adaptive methods have only been applied to bi-objective problems in the past. In this work, we extend the adaptive method based on averages in two ways: (i)~we extend the adaptive method of deriving scalarisation weights for problems with two or more objectives, and (ii)~we use an alternative measure of distance to improve performance. We compare the proposed method with existing ones and show that it leads to the best performance on multi-objective Unconstrained Binary Quadratic Programming (mUBQP) instances with 3 and 4 objectives and that it is competitive with the best one for instances with 2 objectives.

A Study of Scalarisation Techniques for Multi-Objective QUBO Solving

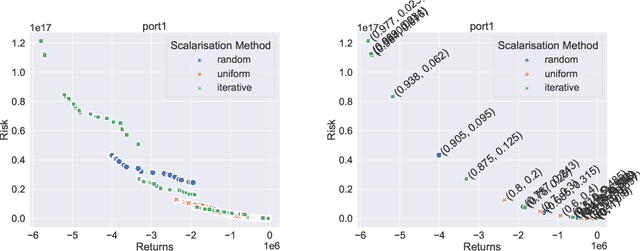
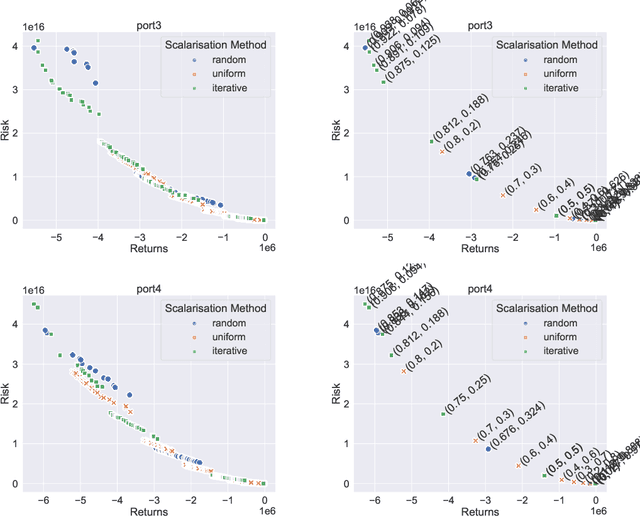
In recent years, there has been significant research interest in solving Quadratic Unconstrained Binary Optimisation (QUBO) problems. Physics-inspired optimisation algorithms have been proposed for deriving optimal or sub-optimal solutions to QUBOs. These methods are particularly attractive within the context of using specialised hardware, such as quantum computers, application specific CMOS and other high performance computing resources for solving optimisation problems. These solvers are then applied to QUBO formulations of combinatorial optimisation problems. Quantum and quantum-inspired optimisation algorithms have shown promising performance when applied to academic benchmarks as well as real-world problems. However, QUBO solvers are single objective solvers. To make them more efficient at solving problems with multiple objectives, a decision on how to convert such multi-objective problems to single-objective problems need to be made. In this study, we compare methods of deriving scalarisation weights when combining two objectives of the cardinality constrained mean-variance portfolio optimisation problem into one. We show significant performance improvement (measured in terms of hypervolume) when using a method that iteratively fills the largest space in the Pareto front compared to a n\"aive approach using uniformly generated weights.

Penalty Weights in QUBO Formulations: Permutation Problems

Optimisation algorithms designed to work on quantum computers or other specialised hardware have been of research interest in recent years. Many of these solver can only optimise problems that are in binary and quadratic form. Quadratic Unconstrained Binary Optimisation (QUBO) is therefore a common formulation used by these solvers. There are many combinatorial optimisation problems that are naturally represented as permutations e.g., travelling salesman problem. Encoding permutation problems using binary variables however presents some challenges. Many QUBO solvers are single flip solvers, it is therefore possible to generate solutions that cannot be decoded to a valid permutation. To create bias towards generating feasible solutions, we use penalty weights. The process of setting static penalty weights for various types of problems is not trivial. This is because values that are too small will lead to infeasible solutions being returned by the solver while values that are too large may lead to slower convergence. In this study, we explore some methods of setting penalty weights within the context of QUBO formulations. We propose new static methods of calculating penalty weights which lead to more promising results than existing methods.

Comparing the Digital Annealer with Classical Evolutionary Algorithm

In more recent years, there has been increasing research interest in exploiting the use of application specific hardware for solving optimisation problems. Examples of solvers that use specialised hardware are IBM's Quantum System One and D-wave's Quantum Annealer (QA) and Fujitsu's Digital Annealer (DA). These solvers have been developed to optimise problems faster than traditional meta-heuristics implemented on general purpose machines. Previous research has shown that these solvers (can optimise many problems much quicker than exact solvers such as GUROBI and CPLEX. Such conclusions have not been made when comparing hardware solvers with classical evolutionary algorithms. Making a fair comparison between traditional evolutionary algorithms, such as Genetic Algorithm (GA), and the DA (or other similar solvers) is challenging because the later benefits from the use of application specific hardware while evolutionary algorithms are often implemented on general-purpose machines. Moreover, quantum or quantum-inspired solvers are limited to solving problems in a specific format. A common formulation used is Quadratic Unconstrained Binary Optimisation (QUBO). Many optimisation problems are however constrained and have natural representations that are non-binary. Converting such problems to QUBO can lead to more problem difficulty and/or larger search space. The question addressed in this paper is whether quantum or quantum-inspired solvers can optimise QUBO transformations of combinatorial optimisation problems faster than classical evolutionary algorithms applied to the same problems in their natural representations. We show that the DA often present better average objective function values than GA on Travelling Salesman, Quadratic Assignment and Multi-dimensional Knapsack Problem instances.

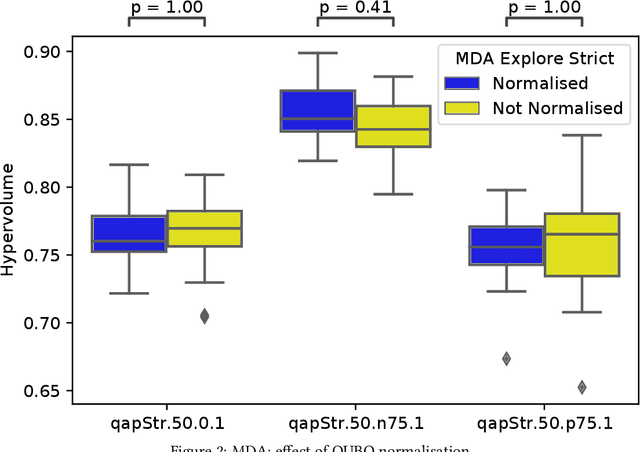
Multi-objective QUBO Solver: Bi-objective Quadratic Assignment

Quantum and quantum-inspired optimisation algorithms are designed to solve problems represented in binary, quadratic and unconstrained form. Combinatorial optimisation problems are therefore often formulated as Quadratic Unconstrained Binary Optimisation Problems (QUBO) to solve them with these algorithms. Moreover, these QUBO solvers are often implemented using specialised hardware to achieve enormous speedups, e.g. Fujitsu's Digital Annealer (DA) and D-Wave's Quantum Annealer. However, these are single-objective solvers, while many real-world problems feature multiple conflicting objectives. Thus, a common practice when using these QUBO solvers is to scalarise such multi-objective problems into a sequence of single-objective problems. Due to design trade-offs of these solvers, formulating each scalarisation may require more time than finding a local optimum. We present the first attempt to extend the algorithm supporting a commercial QUBO solver as a multi-objective solver that is not based on scalarisation. The proposed multi-objective DA algorithm is validated on the bi-objective Quadratic Assignment Problem. We observe that algorithm performance significantly depends on the archiving strategy adopted, and that combining DA with non-scalarisation methods to optimise multiple objectives outperforms the current scalarised version of the DA in terms of final solution quality.