In-Context Learning of Physical Properties: Few-Shot Adaptation to Out-of-Distribution Molecular Graphs

Large language models manifest the ability of few-shot adaptation to a sequence of provided examples. This behavior, known as in-context learning, allows for performing nontrivial machine learning tasks during inference only. In this work, we address the question: can we leverage in-context learning to predict out-of-distribution materials properties? However, this would not be possible for structure property prediction tasks unless an effective method is found to pass atomic-level geometric features to the transformer model. To address this problem, we employ a compound model in which GPT-2 acts on the output of geometry-aware graph neural networks to adapt in-context information. To demonstrate our model's capabilities, we partition the QM9 dataset into sequences of molecules that share a common substructure and use them for in-context learning. This approach significantly improves the performance of the model on out-of-distribution examples, surpassing the one of general graph neural network models.

What if we Increase the Number of Objectives? Theoretical and Empirical Implications for Many-objective Optimization

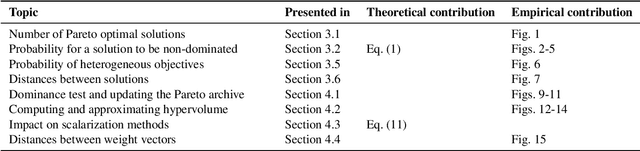
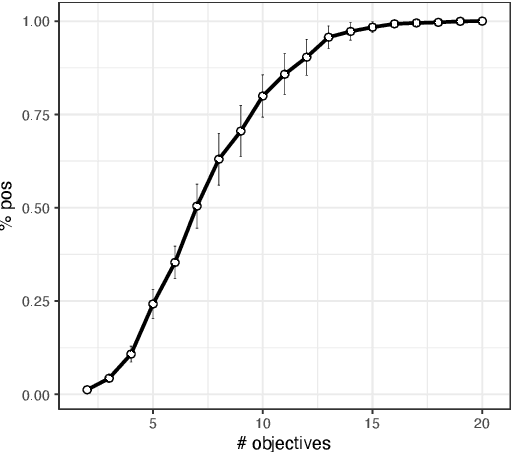
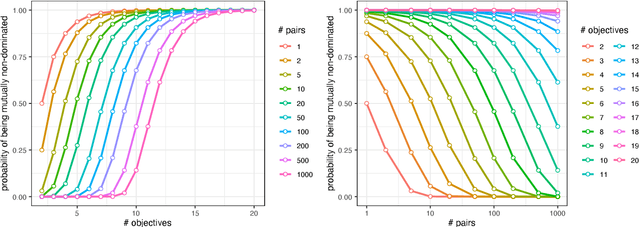
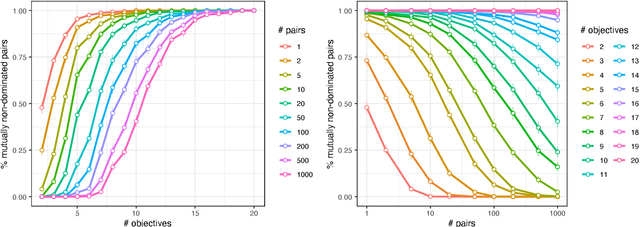
The difficulty of solving a multi-objective optimization problem is impacted by the number of objectives to be optimized. The presence of many objectives typically introduces a number of challenges that affect the choice/design of optimization algorithms. This paper investigates the drivers of these challenges from two angles: (i) the influence of the number of objectives on problem characteristics and (ii) the practical behavior of commonly used procedures and algorithms for coping with many objectives. In addition to reviewing various drivers, the paper makes theoretical contributions by quantifying some drivers and/or verifying these drivers empirically by carrying out experiments on multi-objective NK landscapes and other typical benchmarks. We then make use of our theoretical and empirical findings to derive practical recommendations to support algorithm design. Finally, we discuss remaining theoretical gaps and opportunities for future research in the area of multi- and many-objective optimization.

Improved Quick Hypervolume Algorithm

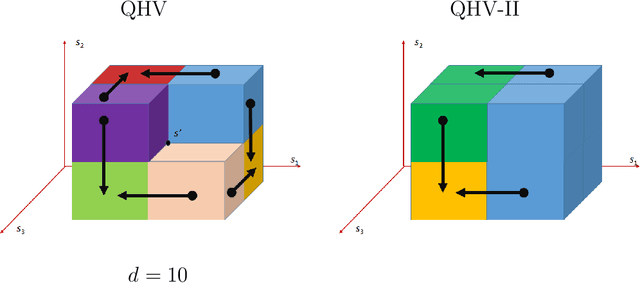
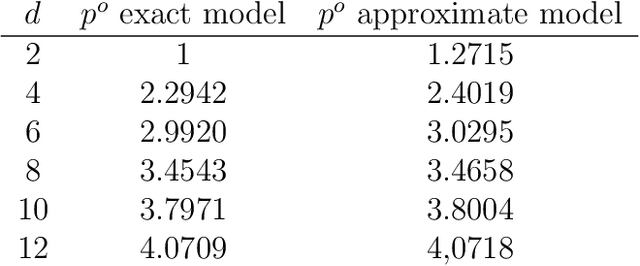
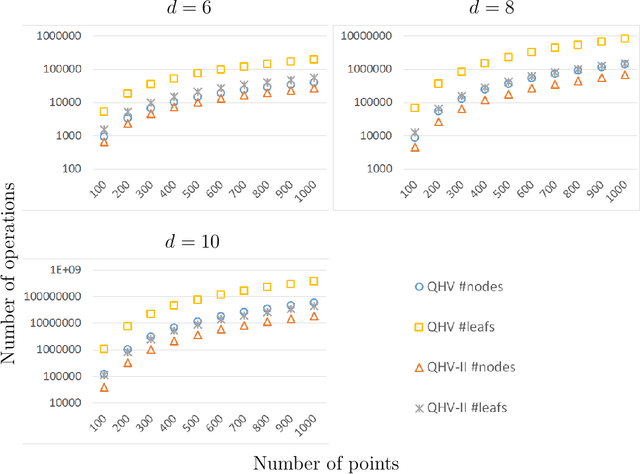
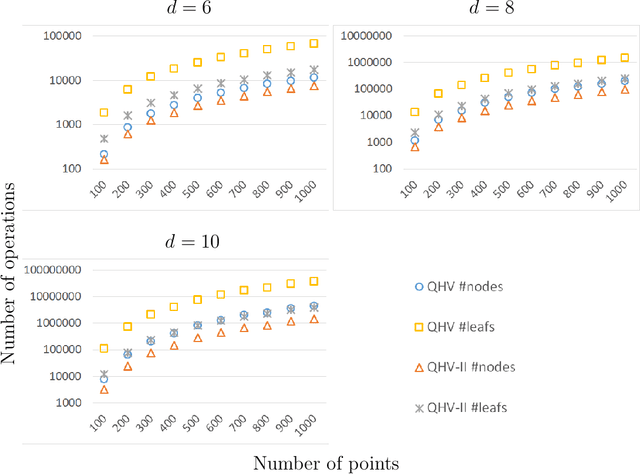
In this paper, we present a significant improvement of Quick Hypervolume algorithm, one of the state-of-the-art algorithms for calculating exact hypervolume of the space dominated by a set of d-dimensional points. This value is often used as a quality indicator in multiobjective evolutionary algorithms and other multiobjective metaheuristics and the efficiency of calculating this indicator is of crucial importance especially in the case of large sets or many dimensional objective spaces. We use a similar divide and conquer scheme as in the original Quick Hypervolume algorithm, but in our algorithm we split the problem into smaller sub-problems in a different way. Through both theoretical analysis and computational study we show that our approach improves computational complexity of the algorithm and practical running times.

Experimental Analysis of Design Elements of Scalarizing Functions-based Multiobjective Evolutionary Algorithms

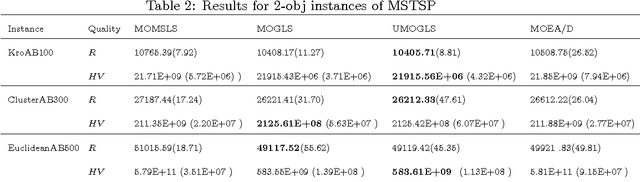
In this paper we systematically study the importance, i.e., the influence on performance, of the main design elements that differentiate scalarizing functions-based multiobjective evolutionary algorithms (MOEAs). This class of MOEAs includes Multiobjecitve Genetic Local Search (MOGLS) and Multiobjective Evolutionary Algorithm Based on Decomposition (MOEA/D) and proved to be very successful in multiple computational experiments and practical applications. The two algorithms share the same common structure and differ only in two main aspects. Using three different multiobjective combinatorial optimization problems, i.e., the multiobjective symmetric traveling salesperson problem, the traveling salesperson problem with profits, and the multiobjective set covering problem, we show that the main differentiating design element is the mechanism for parent selection, while the selection of weight vectors, either random or uniformly distributed, is practically negligible if the number of uniform weight vectors is sufficiently large.