Improved Quick Hypervolume Algorithm
Paper and Code
Aug 11, 2017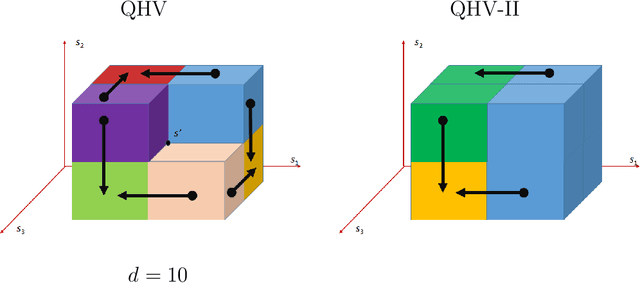
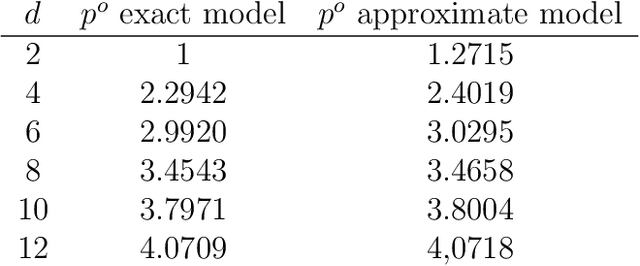
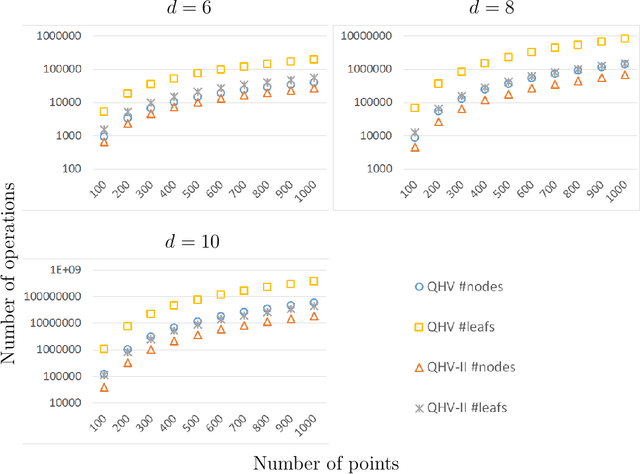
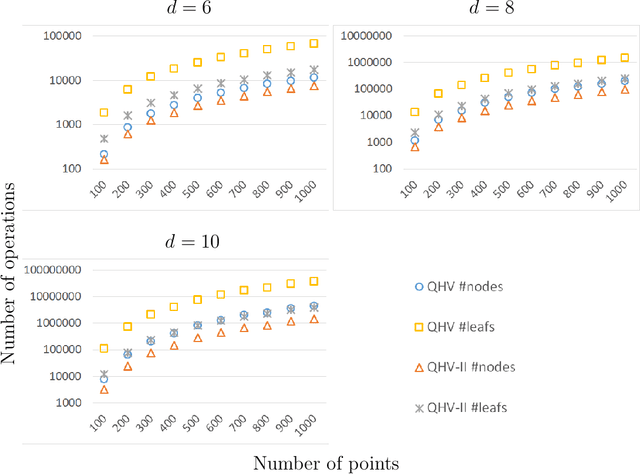
In this paper, we present a significant improvement of Quick Hypervolume algorithm, one of the state-of-the-art algorithms for calculating exact hypervolume of the space dominated by a set of d-dimensional points. This value is often used as a quality indicator in multiobjective evolutionary algorithms and other multiobjective metaheuristics and the efficiency of calculating this indicator is of crucial importance especially in the case of large sets or many dimensional objective spaces. We use a similar divide and conquer scheme as in the original Quick Hypervolume algorithm, but in our algorithm we split the problem into smaller sub-problems in a different way. Through both theoretical analysis and computational study we show that our approach improves computational complexity of the algorithm and practical running times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge