Scalable Hyperbolic Recommender Systems

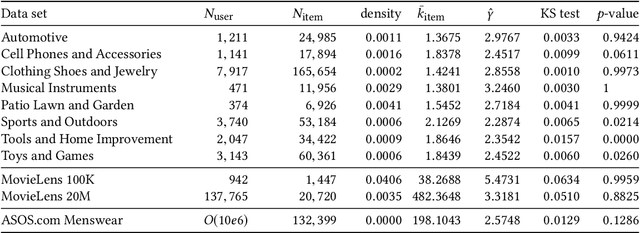
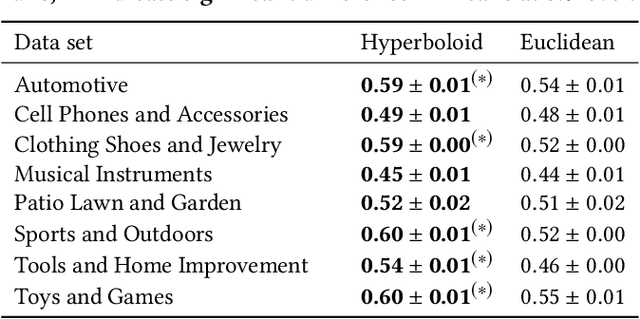
We present a large scale hyperbolic recommender system. We discuss why hyperbolic geometry is a more suitable underlying geometry for many recommendation systems and cover the fundamental milestones and insights that we have gained from its development. In doing so, we demonstrate the viability of hyperbolic geometry for recommender systems, showing that they significantly outperform Euclidean models on datasets with the properties of complex networks. Key to the success of our approach are the novel choice of underlying hyperbolic model and the use of the Einstein midpoint to define an asymmetric recommender system in hyperbolic space. These choices allow us to scale to millions of users and hundreds of thousands of items.

Product Characterisation towards Personalisation: Learning Attributes from Unstructured Data to Recommend Fashion Products

In this paper, we describe a solution to tackle a common set of challenges in e-commerce, which arise from the fact that new products are continually being added to the catalogue. The challenges involve properly personalising the customer experience, forecasting demand and planning the product range. We argue that the foundational piece to solve all of these problems is having consistent and detailed information about each product, information that is rarely available or consistent given the multitude of suppliers and types of products. We describe in detail the architecture and methodology implemented at ASOS, one of the world's largest fashion e-commerce retailers, to tackle this problem. We then show how this quantitative understanding of the products can be leveraged to improve recommendations in a hybrid recommender system approach.

Local Optima Networks: A New Model of Combinatorial Fitness Landscapes

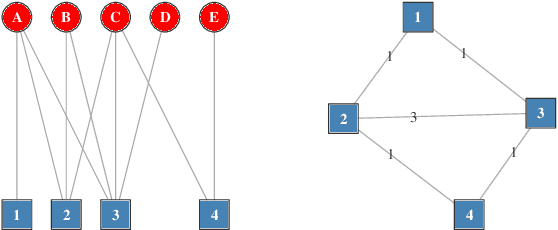
This chapter overviews a recently introduced network-based model of combinatorial landscapes: Local Optima Networks (LON). The model compresses the information given by the whole search space into a smaller mathematical object that is a graph having as vertices the local optima and as edges the possible weighted transitions between them. Two definitions of edges have been proposed: basin-transition and escape-edges, which capture relevant topological features of the underlying search spaces. This network model brings a new set of metrics to characterize the structure of combinatorial landscapes, those associated with the science of complex networks. These metrics are described, and results are presented of local optima network extraction and analysis for two selected combinatorial landscapes: NK landscapes and the quadratic assignment problem. Network features are found to correlate with and even predict the performance of heuristic search algorithms operating on these problems.

Local Optima Networks, Landscape Autocorrelation and Heuristic Search Performance

Recent developments in fitness landscape analysis include the study of Local Optima Networks (LON) and applications of the Elementary Landscapes theory. This paper represents a first step at combining these two tools to explore their ability to forecast the performance of search algorithms. We base our analysis on the Quadratic Assignment Problem (QAP) and conduct a large statistical study over 600 generated instances of different types. Our results reveal interesting links between the network measures, the autocorrelation measures and the performance of heuristic search algorithms.

Local optima networks and the performance of iterated local search

Local Optima Networks (LONs) have been recently proposed as an alternative model of combinatorial fitness landscapes. The model compresses the information given by the whole search space into a smaller mathematical object that is the graph having as vertices the local optima and as edges the possible weighted transitions between them. A new set of metrics can be derived from this model that capture the distribution and connectivity of the local optima in the underlying configuration space. This paper departs from the descriptive analysis of local optima networks, and actively studies the correlation between network features and the performance of a local search heuristic. The NK family of landscapes and the Iterated Local Search metaheuristic are considered. With a statistically-sound approach based on multiple linear regression, it is shown that some LONs' features strongly influence and can even partly predict the performance of a heuristic search algorithm. This study validates the expressive power of LONs as a model of combinatorial fitness landscapes.

Clustering of Local Optima in Combinatorial Fitness Landscapes

Using the recently proposed model of combinatorial landscapes: local optima networks, we study the distribution of local optima in two classes of instances of the quadratic assignment problem. Our results indicate that the two problem instance classes give rise to very different configuration spaces. For the so-called real-like class, the optima networks possess a clear modular structure, while the networks belonging to the class of random uniform instances are less well partitionable into clusters. We briefly discuss the consequences of the findings for heuristically searching the corresponding problem spaces.

Communities of Minima in Local Optima Networks of Combinatorial Spaces

In this work we present a new methodology to study the structure of the configuration spaces of hard combinatorial problems. It consists in building the network that has as nodes the locally optimal configurations and as edges the weighted oriented transitions between their basins of attraction. We apply the approach to the detection of communities in the optima networks produced by two different classes of instances of a hard combinatorial optimization problem: the quadratic assignment problem (QAP). We provide evidence indicating that the two problem instance classes give rise to very different configuration spaces. For the so-called real-like class, the networks possess a clear modular structure, while the optima networks belonging to the class of random uniform instances are less well partitionable into clusters. This is convincingly supported by using several statistical tests. Finally, we shortly discuss the consequences of the findings for heuristically searching the corresponding problem spaces.

Local Optima Networks of the Quadratic Assignment Problem

Using a recently proposed model for combinatorial landscapes, Local Optima Networks (LON), we conduct a thorough analysis of two types of instances of the Quadratic Assignment Problem (QAP). This network model is a reduction of the landscape in which the nodes correspond to the local optima, and the edges account for the notion of adjacency between their basins of attraction. The model was inspired by the notion of 'inherent network' of potential energy surfaces proposed in physical-chemistry. The local optima networks extracted from the so called uniform and real-like QAP instances, show features clearly distinguishing these two types of instances. Apart from a clear confirmation that the search difficulty increases with the problem dimension, the analysis provides new confirming evidence explaining why the real-like instances are easier to solve exactly using heuristic search, while the uniform instances are easier to solve approximately. Although the local optima network model is still under development, we argue that it provides a novel view of combinatorial landscapes, opening up the possibilities for new analytical tools and understanding of problem difficulty in combinatorial optimization.