Fabon Dzogang
A Dataset for Learning Graph Representations to Predict Customer Returns in Fashion Retail
Mar 12, 2023Abstract:We present a novel dataset collected by ASOS (a major online fashion retailer) to address the challenge of predicting customer returns in a fashion retail ecosystem. With the release of this substantial dataset we hope to motivate further collaboration between research communities and the fashion industry. We first explore the structure of this dataset with a focus on the application of Graph Representation Learning in order to exploit the natural data structure and provide statistical insights into particular features within the data. In addition to this, we show examples of a return prediction classification task with a selection of baseline models (i.e. with no intermediate representation learning step) and a graph representation based model. We show that in a downstream return prediction classification task, an F1-score of 0.792 can be found using a Graph Neural Network (GNN), improving upon other models discussed in this work. Alongside this increased F1-score, we also present a lower cross-entropy loss by recasting the data into a graph structure, indicating more robust predictions from a GNN based solution. These results provide evidence that GNNs could provide more impactful and usable classifications than other baseline models on the presented dataset and with this motivation, we hope to encourage further research into graph-based approaches using the ASOS GraphReturns dataset.
* The ASOS GraphReturns dataset can be found at https://osf.io/c793h/. Accepted at FashionXRecSys 2022 workshop. Published Version
Scalable Hyperbolic Recommender Systems
Feb 22, 2019
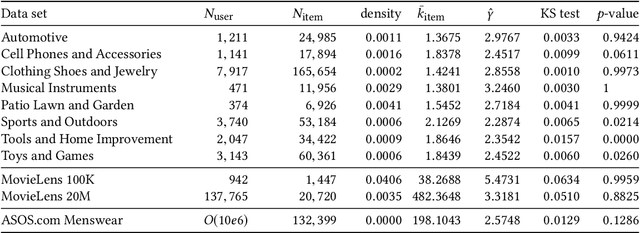
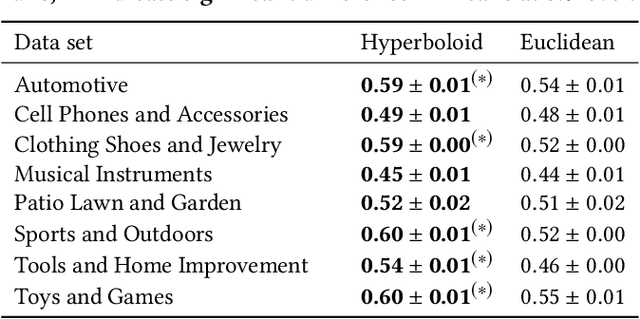
Abstract:We present a large scale hyperbolic recommender system. We discuss why hyperbolic geometry is a more suitable underlying geometry for many recommendation systems and cover the fundamental milestones and insights that we have gained from its development. In doing so, we demonstrate the viability of hyperbolic geometry for recommender systems, showing that they significantly outperform Euclidean models on datasets with the properties of complex networks. Key to the success of our approach are the novel choice of underlying hyperbolic model and the use of the Einstein midpoint to define an asymmetric recommender system in hyperbolic space. These choices allow us to scale to millions of users and hundreds of thousands of items.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge