Optimal Execution Using Reinforcement Learning

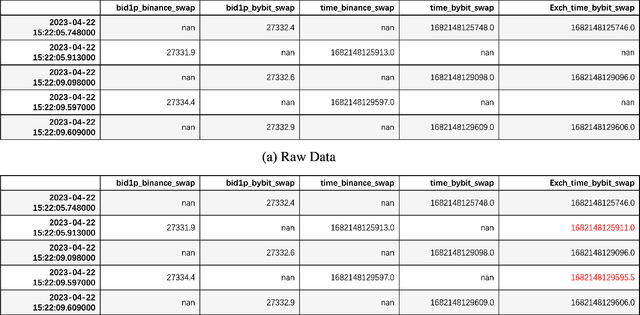
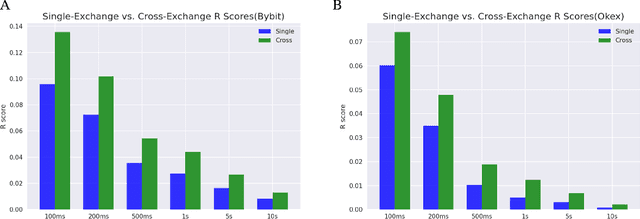
This work is about optimal order execution, where a large order is split into several small orders to maximize the implementation shortfall. Based on the diversity of cryptocurrency exchanges, we attempt to extract cross-exchange signals by aligning data from multiple exchanges for the first time. Unlike most previous studies that focused on using single-exchange information, we discuss the impact of cross-exchange signals on the agent's decision-making in the optimal execution problem. Experimental results show that cross-exchange signals can provide additional information for the optimal execution of cryptocurrency to facilitate the optimal execution process.

Integrating Tick-level Data and Periodical Signal for High-frequency Market Making

We focus on the problem of market making in high-frequency trading. Market making is a critical function in financial markets that involves providing liquidity by buying and selling assets. However, the increasing complexity of financial markets and the high volume of data generated by tick-level trading makes it challenging to develop effective market making strategies. To address this challenge, we propose a deep reinforcement learning approach that fuses tick-level data with periodic prediction signals to develop a more accurate and robust market making strategy. Our results of market making strategies based on different deep reinforcement learning algorithms under the simulation scenarios and real data experiments in the cryptocurrency markets show that the proposed framework outperforms existing methods in terms of profitability and risk management.

A Dataset for Learning Graph Representations to Predict Customer Returns in Fashion Retail

We present a novel dataset collected by ASOS (a major online fashion retailer) to address the challenge of predicting customer returns in a fashion retail ecosystem. With the release of this substantial dataset we hope to motivate further collaboration between research communities and the fashion industry. We first explore the structure of this dataset with a focus on the application of Graph Representation Learning in order to exploit the natural data structure and provide statistical insights into particular features within the data. In addition to this, we show examples of a return prediction classification task with a selection of baseline models (i.e. with no intermediate representation learning step) and a graph representation based model. We show that in a downstream return prediction classification task, an F1-score of 0.792 can be found using a Graph Neural Network (GNN), improving upon other models discussed in this work. Alongside this increased F1-score, we also present a lower cross-entropy loss by recasting the data into a graph structure, indicating more robust predictions from a GNN based solution. These results provide evidence that GNNs could provide more impactful and usable classifications than other baseline models on the presented dataset and with this motivation, we hope to encourage further research into graph-based approaches using the ASOS GraphReturns dataset.

MFAI: A Scalable Bayesian Matrix Factorization Approach to Leveraging Auxiliary Information

In various practical situations, matrix factorization methods suffer from poor data quality, such as high data sparsity and low signal-to-noise ratio (SNR). Here we consider a matrix factorization problem by utilizing auxiliary information, which is massively available in real applications, to overcome the challenges caused by poor data quality. Unlike existing methods that mainly rely on simple linear models to combine auxiliary information with the main data matrix, we propose to integrate gradient boosted trees in the probabilistic matrix factorization framework to effectively leverage auxiliary information (MFAI). Thus, MFAI naturally inherits several salient features of gradient boosted trees, such as the capability of flexibly modeling nonlinear relationships, and robustness to irrelevant features and missing values in auxiliary information. The parameters in MAFI can be automatically determined under the empirical Bayes framework, making it adaptive to the utilization of auxiliary information and immune to overfitting. Moreover, MFAI is computationally efficient and scalable to large-scale datasets by exploiting variational inference. We demonstrate the advantages of MFAI through comprehensive numerical results from simulation studies and real data analysis. Our approach is implemented in the R package mfair available at https://github.com/YangLabHKUST/mfair.

Wiener filters on graphs and distributed polynomial approximation algorithms

In this paper, we consider Wiener filters to reconstruct deterministic and (wide-band) stationary graph signals from their observations corrupted by random noises, and we propose distributed algorithms to implement Wiener filters and inverse filters on networks in which agents are equipped with a data processing subsystem for limited data storage and computation power, and with a one-hop communication subsystem for direct data exchange only with their adjacent agents. The proposed distributed polynomial approximation algorithm is an exponential convergent quasi-Newton method based on Jacobi polynomial approximation and Chebyshev interpolation polynomial approximation to analytic functions on a cube. Our numerical simulations show that Wiener filtering procedure performs better on denoising (wide-band) stationary signals than the Tikhonov regularization approach does, and that the proposed polynomial approximation algorithms converge faster than the Chebyshev polynomial approximation algorithm and gradient decent algorithm do in the implementation of an inverse filtering procedure associated with a polynomial filter of commutative graph shifts.