Learning with Noisy Labels: the Exploration of Error Bounds in Classification

Numerous studies have shown that label noise can lead to poor generalization performance, negatively affecting classification accuracy. Therefore, understanding the effectiveness of classifiers trained using deep neural networks in the presence of noisy labels is of considerable practical significance. In this paper, we focus on the error bounds of excess risks for classification problems with noisy labels within deep learning frameworks. We begin by exploring loss functions with noise-tolerant properties, ensuring that the empirical minimizer on noisy data aligns with that on the true data. Next, we estimate the error bounds of the excess risks, expressed as a sum of statistical error and approximation error. We estimate the statistical error on a dependent (mixing) sequence, bounding it with the help of the associated independent block sequence. For the approximation error, we first express the classifiers as the composition of the softmax function and a continuous function from $[0,1]^d$ to $\mathbb{R}^K$. The main task is then to estimate the approximation error for the continuous function from $[0,1]^d$ to $\mathbb{R}^K$. Finally, we focus on the curse of dimensionality based on the low-dimensional manifold assumption.

UGMathBench: A Diverse and Dynamic Benchmark for Undergraduate-Level Mathematical Reasoning with Large Language Models

Large Language Models (LLMs) have made significant strides in mathematical reasoning, underscoring the need for a comprehensive and fair evaluation of their capabilities. However, existing benchmarks often fall short, either lacking extensive coverage of undergraduate-level mathematical problems or probably suffering from test-set contamination. To address these issues, we introduce UGMathBench, a diverse and dynamic benchmark specifically designed for evaluating undergraduate-level mathematical reasoning with LLMs. UGMathBench comprises 5,062 problems across 16 subjects and 111 topics, featuring 10 distinct answer types. Each problem includes three randomized versions, with additional versions planned for release as leading open-source LLMs become saturated in UGMathBench. Furthermore, we propose two key metrics: effective accuracy (EAcc), which measures the percentage of correctly solved problems across all three versions, and reasoning gap ($\Delta$), which assesses reasoning robustness by calculating the difference between the average accuracy across all versions and EAcc. Our extensive evaluation of 23 leading LLMs reveals that the highest EAcc achieved is 56.3\% by OpenAI-o1-mini, with large $\Delta$ values observed across different models. This highlights the need for future research aimed at developing "large reasoning models" with high EAcc and $\Delta = 0$. We anticipate that the release of UGMathBench, along with its detailed evaluation codes, will serve as a valuable resource to advance the development of LLMs in solving mathematical problems.

Can LLMs Solve longer Math Word Problems Better?

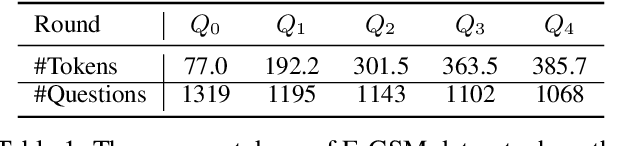
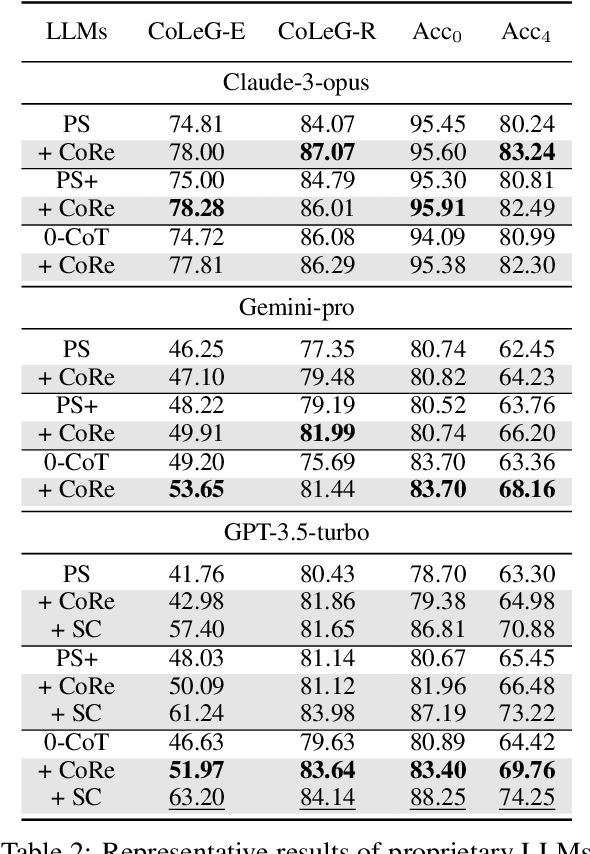
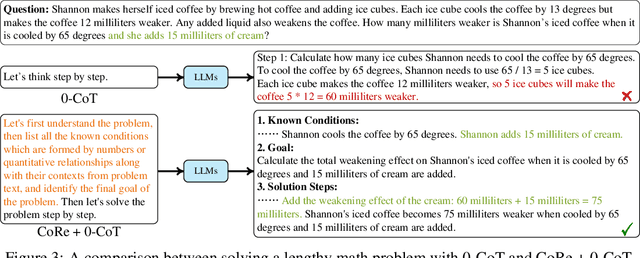
Math Word Problems (MWPs) are crucial for evaluating the capability of Large Language Models (LLMs), with current research primarily focusing on questions with concise contexts. However, as real-world math problems often involve complex circumstances, LLMs' ability to solve long MWPs is vital for their applications in these scenarios, yet remains under-explored. This study pioneers the exploration of Context Length Generalizability (CoLeG), the ability of LLMs to solve long MWPs. We introduce Extended Grade-School Math (E-GSM), a collection of MWPs with lengthy narratives. Two novel metrics are proposed to assess the efficacy and resilience of LLMs in solving these problems. Our examination of existing zero-shot prompting techniques and both proprietary and open-source LLMs reveals a general deficiency in CoLeG. To alleviate these challenges, we propose distinct approaches for different categories of LLMs. For proprietary LLMs, a new instructional prompt is proposed to mitigate the influence of long context. For open-source LLMs, a new data augmentation task is developed to improve CoLeG. Our comprehensive results demonstrate the effectiveness of our proposed methods, showing not only improved performance on E-GSM but also generalizability across several other MWP benchmarks. Our findings pave the way for future research in employing LLMs for complex, real-world applications, offering practical solutions to current limitations and opening avenues for further exploration of model generalizability and training methodologies.

Can We Verify Step by Step for Incorrect Answer Detection?

Chain-of-Thought (CoT) prompting has marked a significant advancement in enhancing the reasoning capabilities of large language models (LLMs). Previous studies have developed various extensions of CoT, which focus primarily on enhancing end-task performance. In addition, there has been research on assessing the quality of reasoning chains in CoT. This raises an intriguing question: Is it possible to predict the accuracy of LLM outputs by scrutinizing the reasoning chains they generate? To answer this research question, we introduce a benchmark, R2PE, designed specifically to explore the relationship between reasoning chains and performance in various reasoning tasks spanning five different domains. This benchmark aims to measure the falsehood of the final output of LLMs based on the reasoning steps. To make full use of information in multiple reasoning chains, we propose the process discernibility score (PDS) framework that beats the answer-checking baseline by a large margin. Concretely, this resulted in an average of 5.1% increase in the F1 score across all 45 subsets within R2PE. We further demonstrate our PDS's efficacy in advancing open-domain QA accuracy. Data and code are available at https://github.com/XinXU-USTC/R2PE.

Reconstructing Close Human Interactions from Multiple Views

This paper addresses the challenging task of reconstructing the poses of multiple individuals engaged in close interactions, captured by multiple calibrated cameras. The difficulty arises from the noisy or false 2D keypoint detections due to inter-person occlusion, the heavy ambiguity in associating keypoints to individuals due to the close interactions, and the scarcity of training data as collecting and annotating motion data in crowded scenes is resource-intensive. We introduce a novel system to address these challenges. Our system integrates a learning-based pose estimation component and its corresponding training and inference strategies. The pose estimation component takes multi-view 2D keypoint heatmaps as input and reconstructs the pose of each individual using a 3D conditional volumetric network. As the network doesn't need images as input, we can leverage known camera parameters from test scenes and a large quantity of existing motion capture data to synthesize massive training data that mimics the real data distribution in test scenes. Extensive experiments demonstrate that our approach significantly surpasses previous approaches in terms of pose accuracy and is generalizable across various camera setups and population sizes. The code is available on our project page: https://github.com/zju3dv/CloseMoCap.

Provable Tensor Completion with Graph Information

Graphs, depicting the interrelations between variables, has been widely used as effective side information for accurate data recovery in various matrix/tensor recovery related applications. In this paper, we study the tensor completion problem with graph information. Current research on graph-regularized tensor completion tends to be task-specific, lacking generality and systematic approaches. Furthermore, a recovery theory to ensure performance remains absent. Moreover, these approaches overlook the dynamic aspects of graphs, treating them as static akin to matrices, even though graphs could exhibit dynamism in tensor-related scenarios. To confront these challenges, we introduce a pioneering framework in this paper that systematically formulates a novel model, theory, and algorithm for solving the dynamic graph regularized tensor completion problem. For the model, we establish a rigorous mathematical representation of the dynamic graph, based on which we derive a new tensor-oriented graph smoothness regularization. By integrating this regularization into a tensor decomposition model based on transformed t-SVD, we develop a comprehensive model simultaneously capturing the low-rank and similarity structure of the tensor. In terms of theory, we showcase the alignment between the proposed graph smoothness regularization and a weighted tensor nuclear norm. Subsequently, we establish assurances of statistical consistency for our model, effectively bridging a gap in the theoretical examination of the problem involving tensor recovery with graph information. In terms of the algorithm, we develop a solution of high effectiveness, accompanied by a guaranteed convergence, to address the resulting model. To showcase the prowess of our proposed model in contrast to established ones, we provide in-depth numerical experiments encompassing synthetic data as well as real-world datasets.

Optimal Execution Using Reinforcement Learning

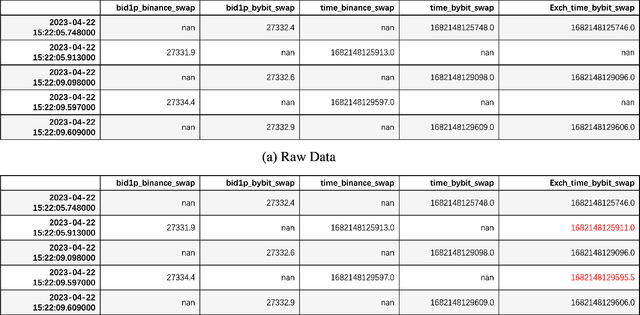
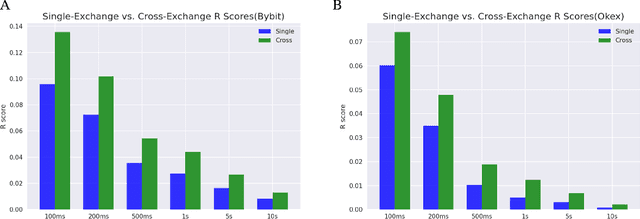
This work is about optimal order execution, where a large order is split into several small orders to maximize the implementation shortfall. Based on the diversity of cryptocurrency exchanges, we attempt to extract cross-exchange signals by aligning data from multiple exchanges for the first time. Unlike most previous studies that focused on using single-exchange information, we discuss the impact of cross-exchange signals on the agent's decision-making in the optimal execution problem. Experimental results show that cross-exchange signals can provide additional information for the optimal execution of cryptocurrency to facilitate the optimal execution process.

Integrating Tick-level Data and Periodical Signal for High-frequency Market Making

We focus on the problem of market making in high-frequency trading. Market making is a critical function in financial markets that involves providing liquidity by buying and selling assets. However, the increasing complexity of financial markets and the high volume of data generated by tick-level trading makes it challenging to develop effective market making strategies. To address this challenge, we propose a deep reinforcement learning approach that fuses tick-level data with periodic prediction signals to develop a more accurate and robust market making strategy. Our results of market making strategies based on different deep reinforcement learning algorithms under the simulation scenarios and real data experiments in the cryptocurrency markets show that the proposed framework outperforms existing methods in terms of profitability and risk management.

MFAI: A Scalable Bayesian Matrix Factorization Approach to Leveraging Auxiliary Information

In various practical situations, matrix factorization methods suffer from poor data quality, such as high data sparsity and low signal-to-noise ratio (SNR). Here we consider a matrix factorization problem by utilizing auxiliary information, which is massively available in real applications, to overcome the challenges caused by poor data quality. Unlike existing methods that mainly rely on simple linear models to combine auxiliary information with the main data matrix, we propose to integrate gradient boosted trees in the probabilistic matrix factorization framework to effectively leverage auxiliary information (MFAI). Thus, MFAI naturally inherits several salient features of gradient boosted trees, such as the capability of flexibly modeling nonlinear relationships, and robustness to irrelevant features and missing values in auxiliary information. The parameters in MAFI can be automatically determined under the empirical Bayes framework, making it adaptive to the utilization of auxiliary information and immune to overfitting. Moreover, MFAI is computationally efficient and scalable to large-scale datasets by exploiting variational inference. We demonstrate the advantages of MFAI through comprehensive numerical results from simulation studies and real data analysis. Our approach is implemented in the R package mfair available at https://github.com/YangLabHKUST/mfair.

Deep Generative Learning via Schrödinger Bridge

We propose to learn a generative model via entropy interpolation with a Schr\"{o}dinger Bridge. The generative learning task can be formulated as interpolating between a reference distribution and a target distribution based on the Kullback-Leibler divergence. At the population level, this entropy interpolation is characterized via an SDE on $[0,1]$ with a time-varying drift term. At the sample level, we derive our Schr\"{o}dinger Bridge algorithm by plugging the drift term estimated by a deep score estimator and a deep density ratio estimator into the Euler-Maruyama method. Under some mild smoothness assumptions of the target distribution, we prove the consistency of both the score estimator and the density ratio estimator, and then establish the consistency of the proposed Schr\"{o}dinger Bridge approach. Our theoretical results guarantee that the distribution learned by our approach converges to the target distribution. Experimental results on multimodal synthetic data and benchmark data support our theoretical findings and indicate that the generative model via Schr\"{o}dinger Bridge is comparable with state-of-the-art GANs, suggesting a new formulation of generative learning. We demonstrate its usefulness in image interpolation and image inpainting.