Xiuwu Liao
Integrating Response Time and Attention Duration in Bayesian Preference Learning for Multiple Criteria Decision Aiding
Apr 21, 2025Abstract:We introduce a multiple criteria Bayesian preference learning framework incorporating behavioral cues for decision aiding. The framework integrates pairwise comparisons, response time, and attention duration to deepen insights into decision-making processes. The approach employs an additive value function model and utilizes a Bayesian framework to derive the posterior distribution of potential ranking models by defining the likelihood of observed preference data and specifying a prior on the preference structure. This distribution highlights each model's ability to reconstruct Decision-Makers' holistic pairwise comparisons. By leveraging both response time as a proxy for cognitive effort and alternative discriminability as well as attention duration as an indicator of criterion importance, the proposed model surpasses traditional methods by uncovering richer behavioral patterns. We report the results of a laboratory experiment on mobile phone contract selection involving 30 real subjects using a dedicated application with time-, eye-, and mouse-tracking components. We validate the novel method's ability to reconstruct complete preferences. The detailed ablation studies reveal time- and attention-related behavioral patterns, confirming that integrating comprehensive data leads to developing models that better align with the DM's actual preferences.
Preference Construction: A Bayesian Interactive Preference Elicitation Framework Based on Monte Carlo Tree Search
Mar 19, 2025Abstract:We present a novel preference learning framework to capture participant preferences efficiently within limited interaction rounds. It involves three main contributions. First, we develop a variational Bayesian approach to infer the participant's preference model by estimating posterior distributions and managing uncertainty from limited information. Second, we propose an adaptive questioning policy that maximizes cumulative uncertainty reduction, formulating questioning as a finite Markov decision process and using Monte Carlo Tree Search to prioritize promising question trajectories. By considering long-term effects and leveraging the efficiency of the Bayesian approach, the policy avoids shortsightedness. Third, we apply the framework to Multiple Criteria Decision Aiding, with pairwise comparison as the preference information and an additive value function as the preference model. We integrate the reparameterization trick to address high-variance issues, enhancing robustness and efficiency. Computational studies on real-world and synthetic datasets demonstrate the framework's practical usability, outperforming baselines in capturing preferences and achieving superior uncertainty reduction within limited interactions.
Matrix Completion with Graph Information: A Provable Nonconvex Optimization Approach
Feb 12, 2025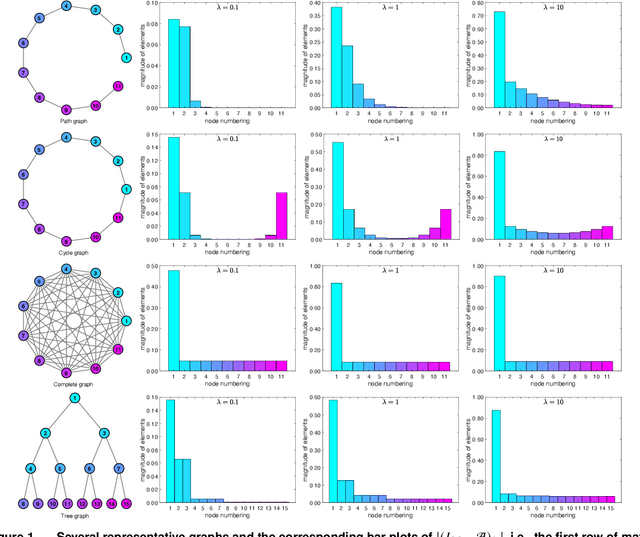
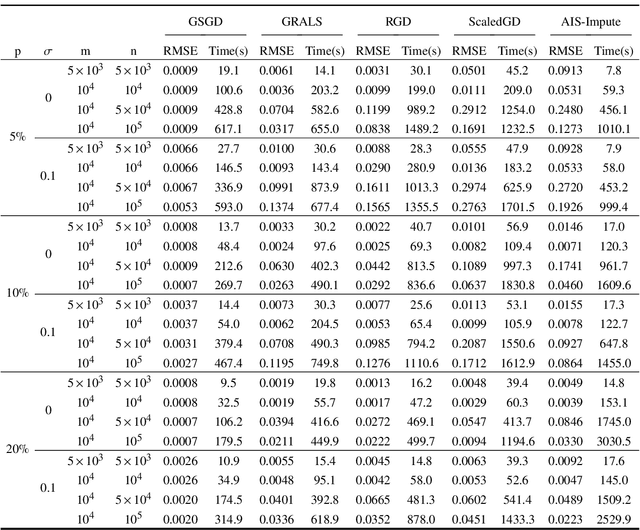
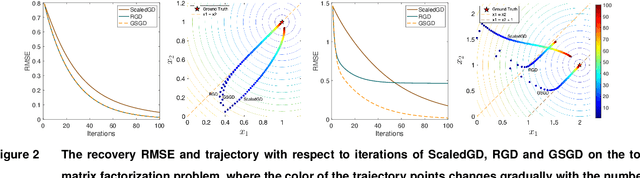

Abstract:We consider the problem of matrix completion with graphs as side information depicting the interrelations between variables. The key challenge lies in leveraging the similarity structure of the graph to enhance matrix recovery. Existing approaches, primarily based on graph Laplacian regularization, suffer from several limitations: (1) they focus only on the similarity between neighboring variables, while overlooking long-range correlations; (2) they are highly sensitive to false edges in the graphs and (3) they lack theoretical guarantees regarding statistical and computational complexities. To address these issues, we propose in this paper a novel graph regularized matrix completion algorithm called GSGD, based on preconditioned projected gradient descent approach. We demonstrate that GSGD effectively captures the higher-order correlation information behind the graphs, and achieves superior robustness and stability against the false edges. Theoretically, we prove that GSGD achieves linear convergence to the global optimum with near-optimal sample complexity, providing the first theoretical guarantees for both recovery accuracy and efficacy in the perspective of nonconvex optimization. Our numerical experiments on both synthetic and real-world data further validate that GSGD achieves superior recovery accuracy and scalability compared with several popular alternatives.
Provable Tensor Completion with Graph Information
Oct 04, 2023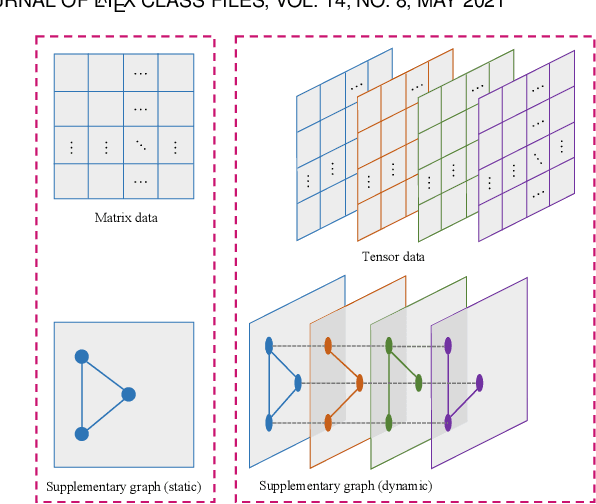


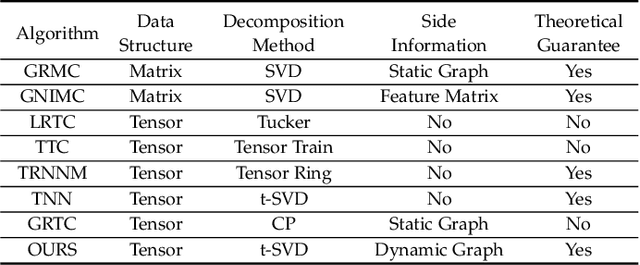
Abstract:Graphs, depicting the interrelations between variables, has been widely used as effective side information for accurate data recovery in various matrix/tensor recovery related applications. In this paper, we study the tensor completion problem with graph information. Current research on graph-regularized tensor completion tends to be task-specific, lacking generality and systematic approaches. Furthermore, a recovery theory to ensure performance remains absent. Moreover, these approaches overlook the dynamic aspects of graphs, treating them as static akin to matrices, even though graphs could exhibit dynamism in tensor-related scenarios. To confront these challenges, we introduce a pioneering framework in this paper that systematically formulates a novel model, theory, and algorithm for solving the dynamic graph regularized tensor completion problem. For the model, we establish a rigorous mathematical representation of the dynamic graph, based on which we derive a new tensor-oriented graph smoothness regularization. By integrating this regularization into a tensor decomposition model based on transformed t-SVD, we develop a comprehensive model simultaneously capturing the low-rank and similarity structure of the tensor. In terms of theory, we showcase the alignment between the proposed graph smoothness regularization and a weighted tensor nuclear norm. Subsequently, we establish assurances of statistical consistency for our model, effectively bridging a gap in the theoretical examination of the problem involving tensor recovery with graph information. In terms of the algorithm, we develop a solution of high effectiveness, accompanied by a guaranteed convergence, to address the resulting model. To showcase the prowess of our proposed model in contrast to established ones, we provide in-depth numerical experiments encompassing synthetic data as well as real-world datasets.
Efficient Fraud Detection using Deep Boosting Decision Trees
Feb 12, 2023Abstract:Fraud detection is to identify, monitor, and prevent potentially fraudulent activities from complex data. The recent development and success in AI, especially machine learning, provides a new data-driven way to deal with fraud. From a methodological point of view, machine learning based fraud detection can be divided into two categories, i.e., conventional methods (decision tree, boosting...) and deep learning, both of which have significant limitations in terms of the lack of representation learning ability for the former and interpretability for the latter. Furthermore, due to the rarity of detected fraud cases, the associated data is usually imbalanced, which seriously degrades the performance of classification algorithms. In this paper, we propose deep boosting decision trees (DBDT), a novel approach for fraud detection based on gradient boosting and neural networks. In order to combine the advantages of both conventional methods and deep learning, we first construct soft decision tree (SDT), a decision tree structured model with neural networks as its nodes, and then ensemble SDTs using the idea of gradient boosting. In this way we embed neural networks into gradient boosting to improve its representation learning capability and meanwhile maintain the interpretability. Furthermore, aiming at the rarity of detected fraud cases, in the model training phase we propose a compositional AUC maximization approach to deal with data imbalances at algorithm level. Extensive experiments on several real-life fraud detection datasets show that DBDT can significantly improve the performance and meanwhile maintain good interpretability. Our code is available at https://github.com/freshmanXB/DBDT.
An Improved Frequent Directions Algorithm for Low-Rank Approximation via Block Krylov Iteration
Sep 24, 2021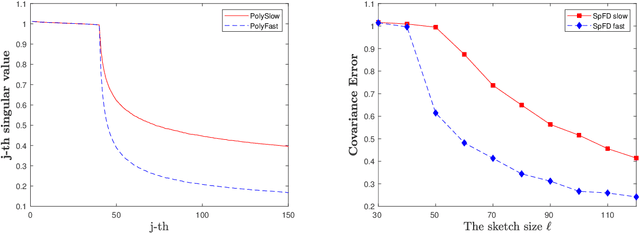
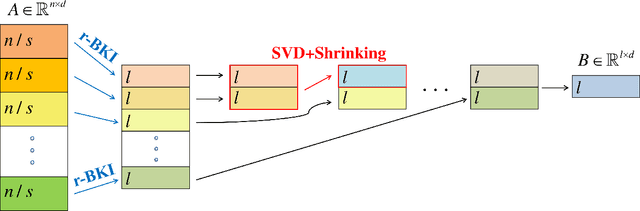
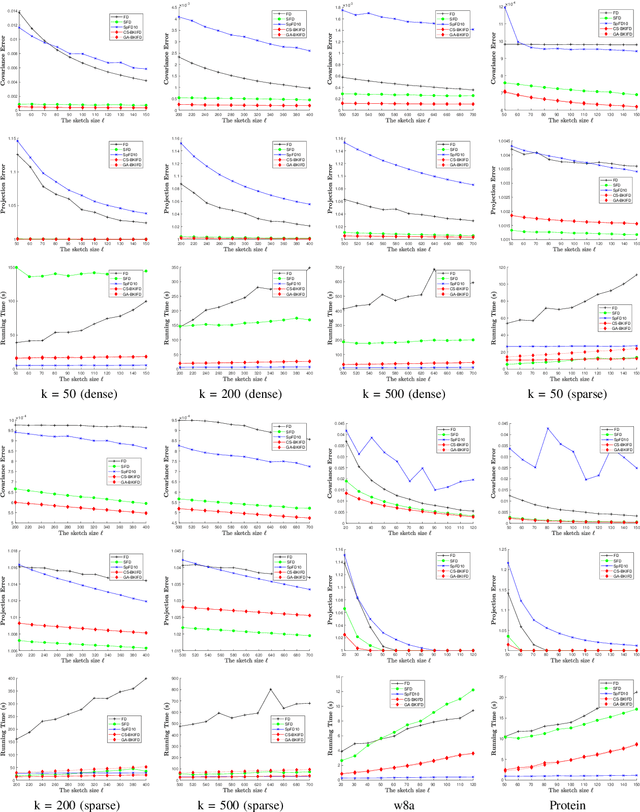
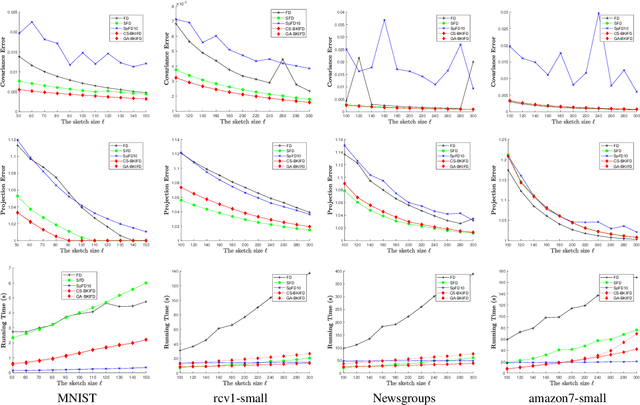
Abstract:Frequent Directions, as a deterministic matrix sketching technique, has been proposed for tackling low-rank approximation problems. This method has a high degree of accuracy and practicality, but experiences a lot of computational cost for large-scale data. Several recent works on the randomized version of Frequent Directions greatly improve the computational efficiency, but unfortunately sacrifice some precision. To remedy such issue, this paper aims to find a more accurate projection subspace to further improve the efficiency and effectiveness of the existing Frequent Directions techniques. Specifically, by utilizing the power of Block Krylov Iteration and random projection technique, this paper presents a fast and accurate Frequent Directions algorithm named as r-BKIFD. The rigorous theoretical analysis shows that the proposed r-BKIFD has a comparable error bound with original Frequent Directions, and the approximation error can be arbitrarily small when the number of iterations is chosen appropriately. Extensive experimental results on both synthetic and real data further demonstrate the superiority of r-BKIFD over several popular Frequent Directions algorithms, both in terms of computational efficiency and accuracy.
An interpretable neural network model through piecewise linear approximation
Jan 20, 2020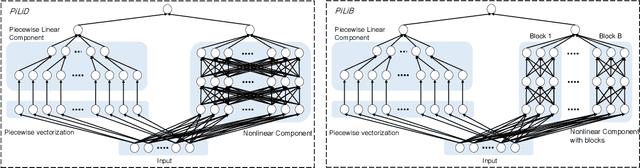
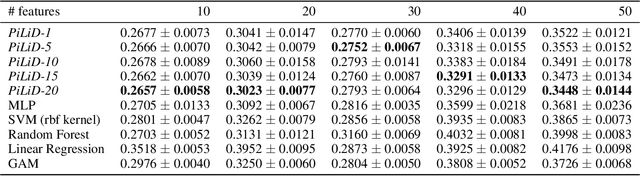

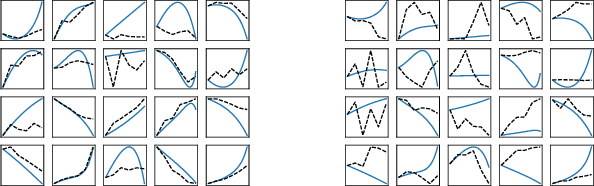
Abstract:Most existing interpretable methods explain a black-box model in a post-hoc manner, which uses simpler models or data analysis techniques to interpret the predictions after the model is learned. However, they (a) may derive contradictory explanations on the same predictions given different methods and data samples, and (b) focus on using simpler models to provide higher descriptive accuracy at the sacrifice of prediction accuracy. To address these issues, we propose a hybrid interpretable model that combines a piecewise linear component and a nonlinear component. The first component describes the explicit feature contributions by piecewise linear approximation to increase the expressiveness of the model. The other component uses a multi-layer perceptron to capture feature interactions and implicit nonlinearity, and increase the prediction performance. Different from the post-hoc approaches, the interpretability is obtained once the model is learned in the form of feature shapes. We also provide a variant to explore higher-order interactions among features to demonstrate that the proposed model is flexible for adaptation. Experiments demonstrate that the proposed model can achieve good interpretability by describing feature shapes while maintaining state-of-the-art accuracy.
Explainable Ordinal Factorization Model: Deciphering the Effects of Attributes by Piece-wise Linear Approximation
Nov 14, 2019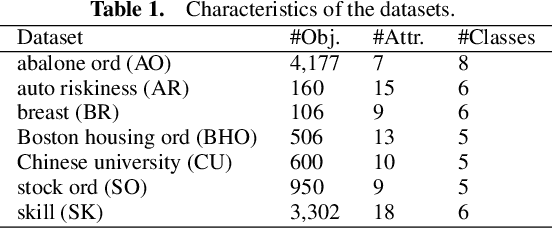
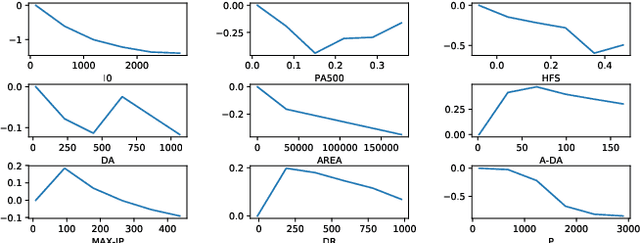

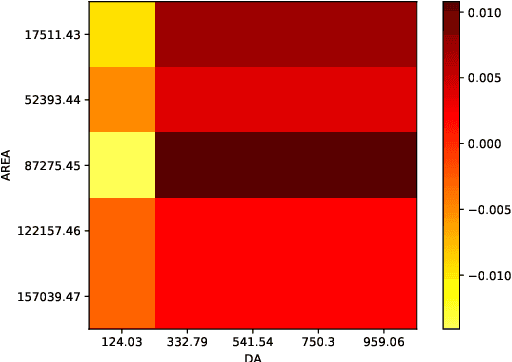
Abstract:Ordinal regression predicts the objects' labels that exhibit a natural ordering, which is important to many managerial problems such as credit scoring and clinical diagnosis. In these problems, the ability to explain how the attributes affect the prediction is critical to users. However, most, if not all, existing ordinal regression models simplify such explanation in the form of constant coefficients for the main and interaction effects of individual attributes. Such explanation cannot characterize the contributions of attributes at different value scales. To address this challenge, we propose a new explainable ordinal regression model, namely, the Explainable Ordinal Factorization Model (XOFM). XOFM uses the piece-wise linear functions to approximate the actual contributions of individual attributes and their interactions. Moreover, XOFM introduces a novel ordinal transformation process to assign each object the probabilities of belonging to multiple relevant classes, instead of fixing boundaries to differentiate classes. XOFM is based on the Factorization Machines to handle the potential sparsity problem as a result of discretizing the attribute scales. Comprehensive experiments with benchmark datasets and baseline models demonstrate that the proposed XOFM exhibits superior explainability and leads to state-of-the-art prediction accuracy.
A preference learning framework for multiple criteria sorting with diverse additive value models and valued assignment examples
Oct 12, 2019
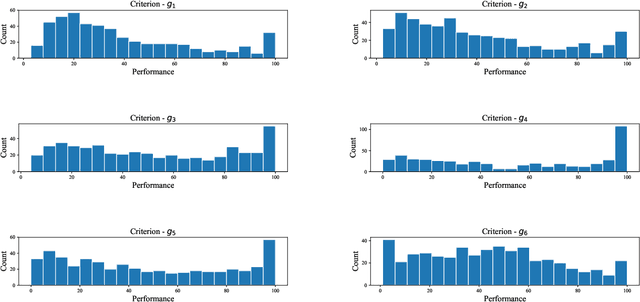

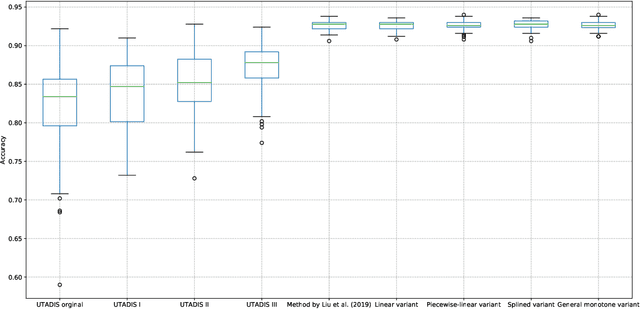
Abstract:We present a preference learning framework for multiple criteria sorting. We consider sorting procedures applying an additive value model with diverse types of marginal value functions (including linear, piecewise-linear, splined, and general monotone ones) under a unified analytical framework. Differently from the existing sorting methods that infer a preference model from crisp decision examples, where each reference alternative is assigned to a unique class, our framework allows to consider valued assignment examples in which a reference alternative can be classified into multiple classes with respective credibility degrees. We propose an optimization model for constructing a preference model from such valued examples by maximizing the credible consistency among reference alternatives. To improve the predictive ability of the constructed model on new instances, we employ the regularization techniques. Moreover, to enhance the capability of addressing large-scale datasets, we introduce a state-of-the-art algorithm that is widely used in the machine learning community to solve the proposed optimization model in a computationally efficient way. Using the constructed additive value model, we determine both crisp and valued assignments for non-reference alternatives. Moreover, we allow the Decision Maker to prioritize importance of classes and give the method a flexibility to adjust classification performance across classes according to the specified priorities. The practical usefulness of the analytical framework is demonstrated on a real-world dataset by comparing it to several existing sorting methods.
An interpretable machine learning framework for modelling human decision behavior
Jun 04, 2019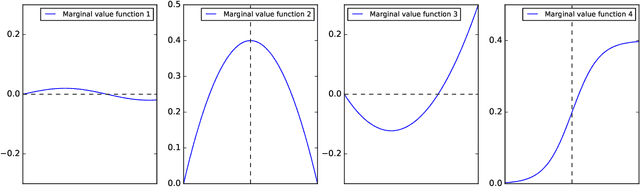
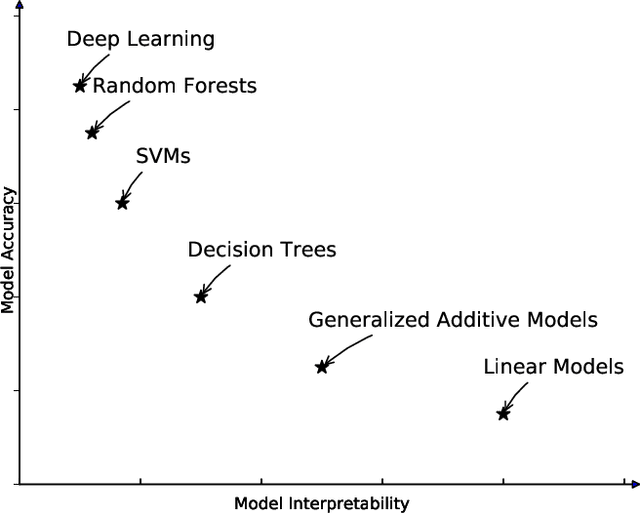
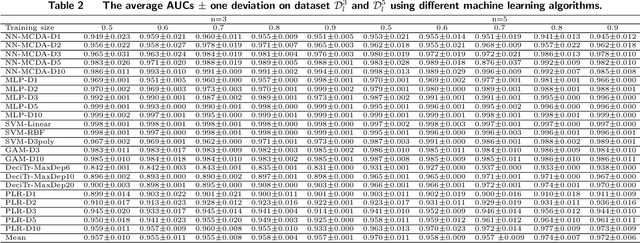
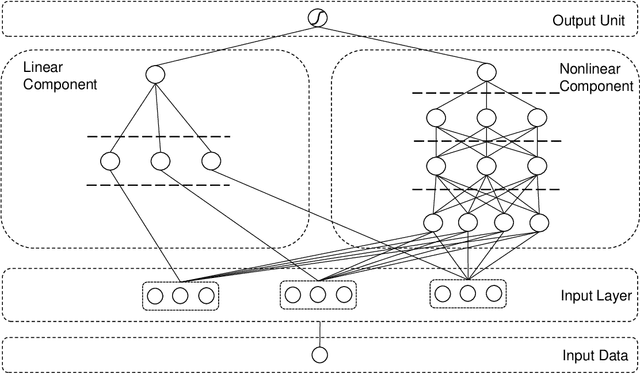
Abstract:Machine learning has recently been widely adopted to address the managerial decision making problems. However, there is a trade-off between performance and interpretability. Full complexity models (such as neural network-based models) are non-traceable black-box, whereas classic interpretable models (such as logistic regression) are usually simplified with lower accuracy. This trade-off limits the application of state-of-the-art machine learning models in management problems, which requires high prediction performance, as well as the understanding of individual attributes' contributions to the model outcome. Multiple criteria decision aiding (MCDA) is a family of interpretable approaches to depicting the rationale of human decision behavior. It is also limited by strong assumptions (e.g. preference independence). In this paper, we propose an interpretable machine learning approach, namely Neural Network-based Multiple Criteria Decision Aiding (NN-MCDA), which combines an additive MCDA model and a fully-connected multilayer perceptron (MLP) to achieve good performance while preserving a certain degree of interpretability. NN-MCDA has a linear component (in an additive form of a set of polynomial functions) to capture the detailed relationship between individual attributes and the prediction, and a nonlinear component (in a standard MLP form) to capture the high-order interactions between attributes and their complex nonlinear transformations. We demonstrate the effectiveness of NN-MCDA with extensive simulation studies and two real-world datasets. To the best of our knowledge, this research is the first to enhance the interpretability of machine learning models with MCDA techniques. The proposed framework also sheds light on how to use machine learning techniques to free MCDA from strong assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge