A preference learning framework for multiple criteria sorting with diverse additive value models and valued assignment examples

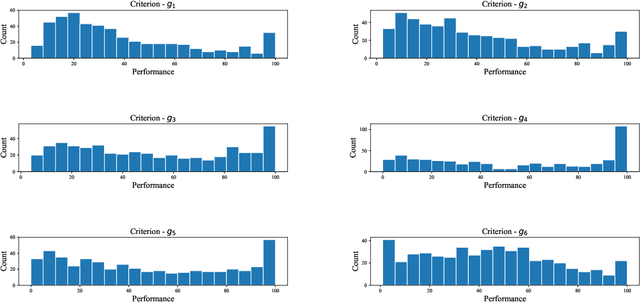
We present a preference learning framework for multiple criteria sorting. We consider sorting procedures applying an additive value model with diverse types of marginal value functions (including linear, piecewise-linear, splined, and general monotone ones) under a unified analytical framework. Differently from the existing sorting methods that infer a preference model from crisp decision examples, where each reference alternative is assigned to a unique class, our framework allows to consider valued assignment examples in which a reference alternative can be classified into multiple classes with respective credibility degrees. We propose an optimization model for constructing a preference model from such valued examples by maximizing the credible consistency among reference alternatives. To improve the predictive ability of the constructed model on new instances, we employ the regularization techniques. Moreover, to enhance the capability of addressing large-scale datasets, we introduce a state-of-the-art algorithm that is widely used in the machine learning community to solve the proposed optimization model in a computationally efficient way. Using the constructed additive value model, we determine both crisp and valued assignments for non-reference alternatives. Moreover, we allow the Decision Maker to prioritize importance of classes and give the method a flexibility to adjust classification performance across classes according to the specified priorities. The practical usefulness of the analytical framework is demonstrated on a real-world dataset by comparing it to several existing sorting methods.

Data-driven preference learning methods for value-driven multiple criteria sorting with interacting criteria

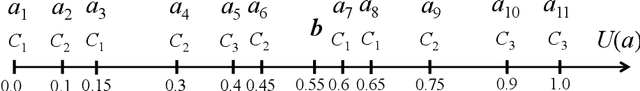
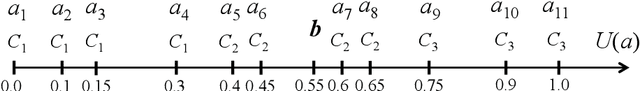
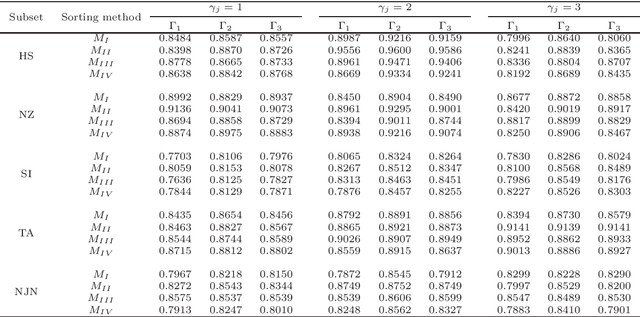
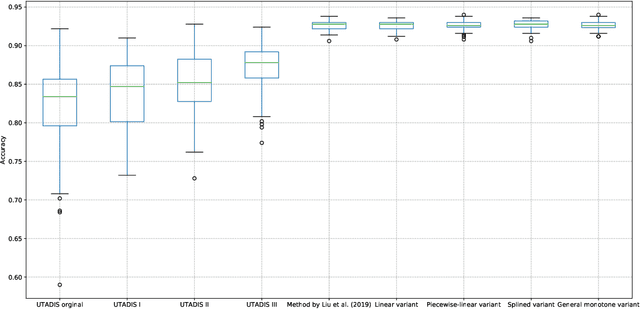
The learning of predictive models for data-driven decision support has been a prevalent topic in many fields. However, construction of models that would capture interactions among input variables is a challenging task. In this paper, we present a new preference learning approach for multiple criteria sorting with potentially interacting criteria. It employs an additive piecewise-linear value function as the basic preference model, which is augmented with components for handling the interactions. To construct such a model from a given set of assignment examples concerning reference alternatives, we develop a convex quadratic programming model. Since its complexity does not depend on the number of training samples, the proposed approach is capable for dealing with data-intensive tasks. To improve the generalization of the constructed model on new instances and to overcome the problem of over-fitting, we employ the regularization techniques. We also propose a few novel methods for classifying non-reference alternatives in order to enhance the applicability of our approach to different datasets. The practical usefulness of the proposed method is demonstrated on a problem of parametric evaluation of research units, whereas its predictive performance is studied on several monotone learning datasets. The experimental results indicate that our approach compares favourably with the classical UTADIS method and the Choquet integral-based sorting model.

Using a Segmenting Description approach in Multiple Criteria Decision Aiding

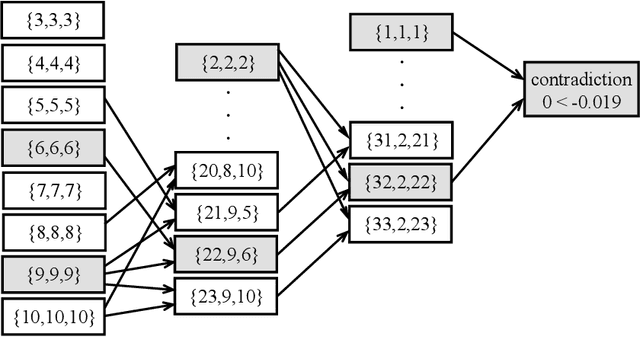
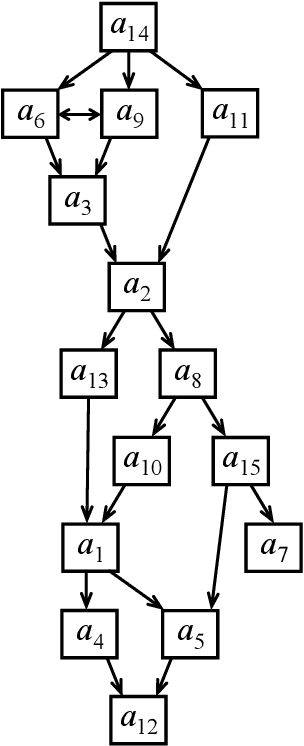
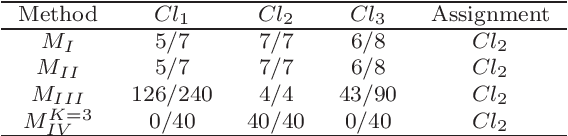
We propose a new method for analyzing a set of parameters in a multiple criteria ranking method. Unlike the existing techniques, we do not use any optimization technique, instead incorporating and extending a Segmenting Description approach. While considering a value-based preference disaggregation method, we demonstrate the usefulness of the introduced algorithm in a multi-purpose decision analysis exploiting a system of inequalities that models the Decision Maker's preferences. Specifically, we discuss how it can be applied for verifying the consistency between the revealed and estimated preferences as well as for identifying the sources of potential incoherence. Moreover, we employ the method for conducting robustness analysis, i.e., discovering a set of all compatible parameter values and verifying the stability of suggested recommendation in view of multiplicity of feasible solutions. In addition, we make clear its suitability for generating arguments about the validity of outcomes and the role of particular criteria. We discuss the favorable characteristics of the Segmenting Description approach which enhance its suitability for use in Multiple Criteria Decision Aiding. These include keeping in memory an entire process of transforming a system of inequalities and avoiding the need for processing the inequalities contained in the basic system which is subsequently enriched with some hypothesis to be verified. The applicability of the proposed method is exemplified on a numerical study.