Data-driven preference learning methods for value-driven multiple criteria sorting with interacting criteria
Paper and Code
May 21, 2019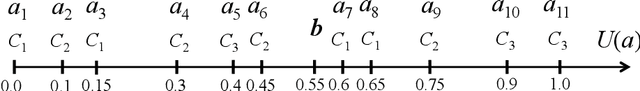
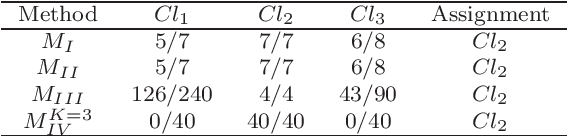
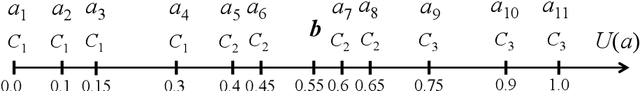
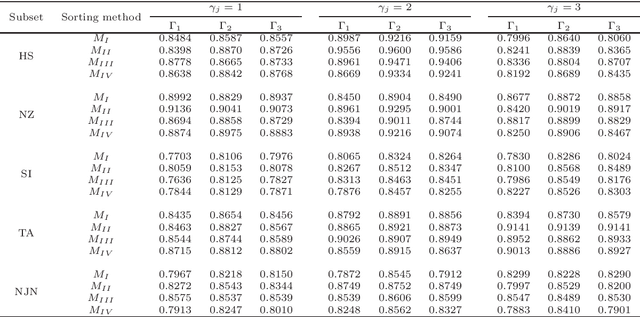
The learning of predictive models for data-driven decision support has been a prevalent topic in many fields. However, construction of models that would capture interactions among input variables is a challenging task. In this paper, we present a new preference learning approach for multiple criteria sorting with potentially interacting criteria. It employs an additive piecewise-linear value function as the basic preference model, which is augmented with components for handling the interactions. To construct such a model from a given set of assignment examples concerning reference alternatives, we develop a convex quadratic programming model. Since its complexity does not depend on the number of training samples, the proposed approach is capable for dealing with data-intensive tasks. To improve the generalization of the constructed model on new instances and to overcome the problem of over-fitting, we employ the regularization techniques. We also propose a few novel methods for classifying non-reference alternatives in order to enhance the applicability of our approach to different datasets. The practical usefulness of the proposed method is demonstrated on a problem of parametric evaluation of research units, whereas its predictive performance is studied on several monotone learning datasets. The experimental results indicate that our approach compares favourably with the classical UTADIS method and the Choquet integral-based sorting model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge