Qianxin Yi
Efficient Generalized Low-Rank Tensor Contextual Bandits
Nov 09, 2023



Abstract:In this paper, we aim to build a novel bandits algorithm that is capable of fully harnessing the power of multi-dimensional data and the inherent non-linearity of reward functions to provide high-usable and accountable decision-making services. To this end, we introduce a generalized low-rank tensor contextual bandits model in which an action is formed from three feature vectors, and thus can be represented by a tensor. In this formulation, the reward is determined through a generalized linear function applied to the inner product of the action's feature tensor and a fixed but unknown parameter tensor with a low tubal rank. To effectively achieve the trade-off between exploration and exploitation, we introduce a novel algorithm called "Generalized Low-Rank Tensor Exploration Subspace then Refine" (G-LowTESTR). This algorithm first collects raw data to explore the intrinsic low-rank tensor subspace information embedded in the decision-making scenario, and then converts the original problem into an almost lower-dimensional generalized linear contextual bandits problem. Rigorous theoretical analysis shows that the regret bound of G-LowTESTR is superior to those in vectorization and matricization cases. We conduct a series of simulations and real data experiments to further highlight the effectiveness of G-LowTESTR, leveraging its ability to capitalize on the low-rank tensor structure for enhanced learning.
An Improved Frequent Directions Algorithm for Low-Rank Approximation via Block Krylov Iteration
Sep 24, 2021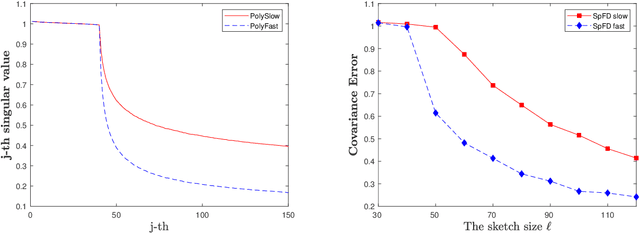
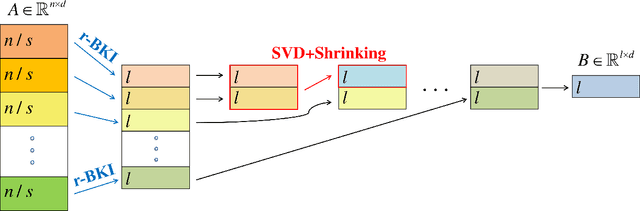
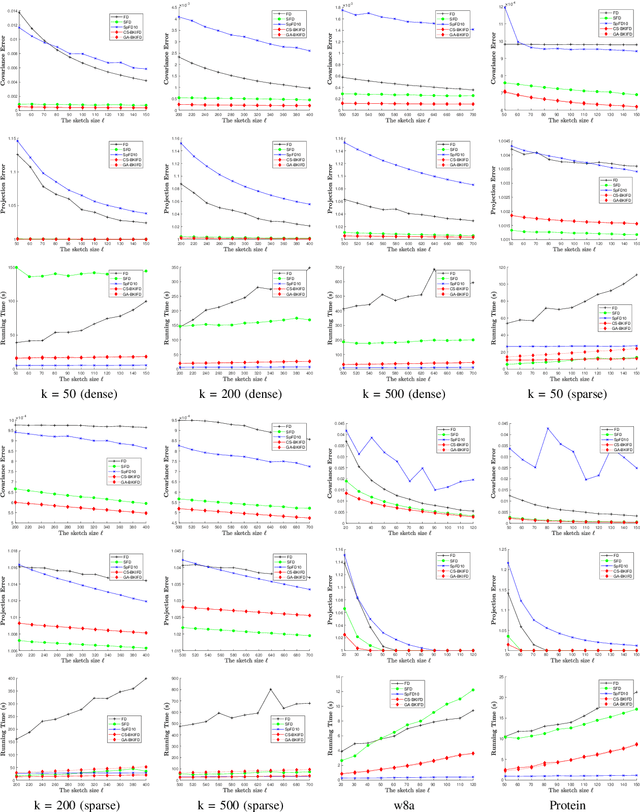
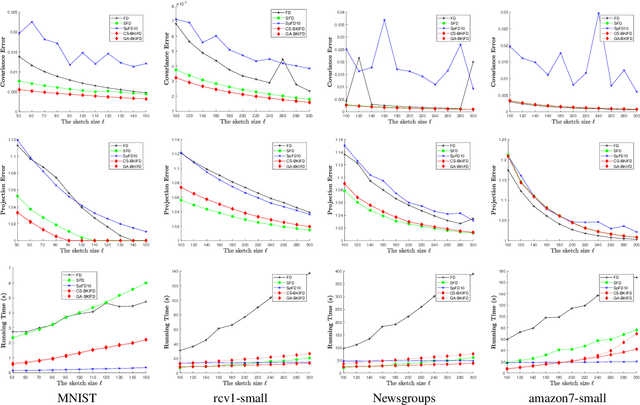
Abstract:Frequent Directions, as a deterministic matrix sketching technique, has been proposed for tackling low-rank approximation problems. This method has a high degree of accuracy and practicality, but experiences a lot of computational cost for large-scale data. Several recent works on the randomized version of Frequent Directions greatly improve the computational efficiency, but unfortunately sacrifice some precision. To remedy such issue, this paper aims to find a more accurate projection subspace to further improve the efficiency and effectiveness of the existing Frequent Directions techniques. Specifically, by utilizing the power of Block Krylov Iteration and random projection technique, this paper presents a fast and accurate Frequent Directions algorithm named as r-BKIFD. The rigorous theoretical analysis shows that the proposed r-BKIFD has a comparable error bound with original Frequent Directions, and the approximation error can be arbitrarily small when the number of iterations is chosen appropriately. Extensive experimental results on both synthetic and real data further demonstrate the superiority of r-BKIFD over several popular Frequent Directions algorithms, both in terms of computational efficiency and accuracy.
Effective Streaming Low-tubal-rank Tensor Approximation via Frequent Directions
Aug 23, 2021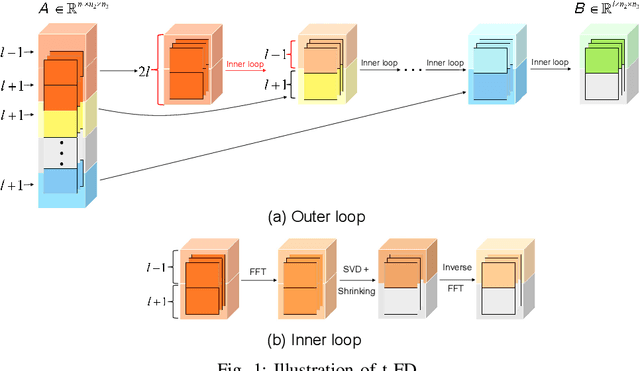
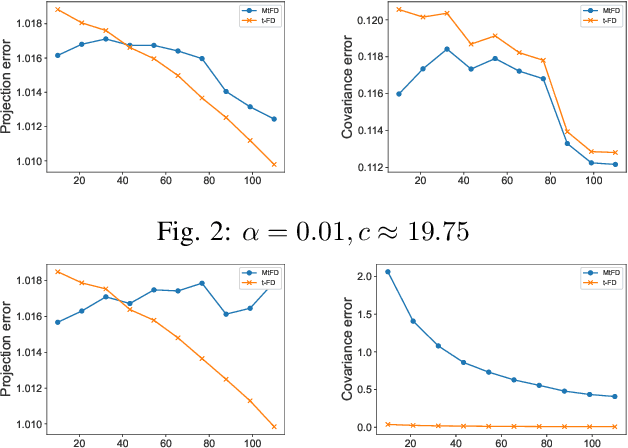
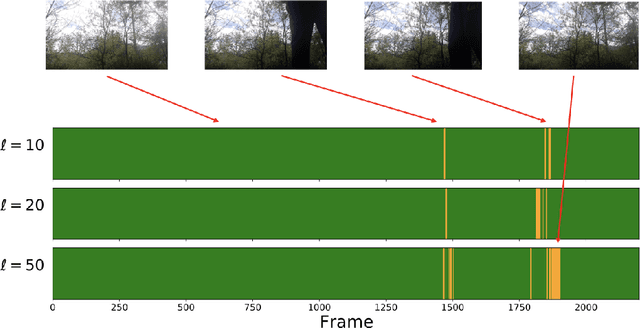
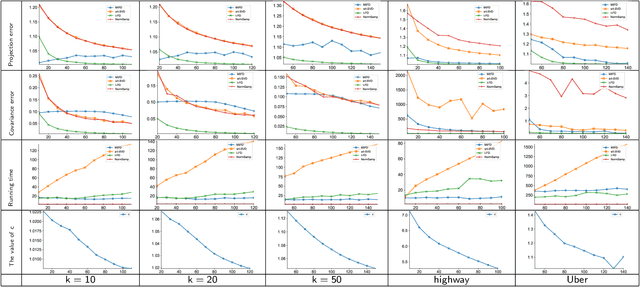
Abstract:Low-tubal-rank tensor approximation has been proposed to analyze large-scale and multi-dimensional data. However, finding such an accurate approximation is challenging in the streaming setting, due to the limited computational resources. To alleviate this issue, this paper extends a popular matrix sketching technique, namely Frequent Directions, for constructing an efficient and accurate low-tubal-rank tensor approximation from streaming data based on the tensor Singular Value Decomposition (t-SVD). Specifically, the new algorithm allows the tensor data to be observed slice by slice, but only needs to maintain and incrementally update a much smaller sketch which could capture the principal information of the original tensor. The rigorous theoretical analysis shows that the approximation error of the new algorithm can be arbitrarily small when the sketch size grows linearly. Extensive experimental results on both synthetic and real multi-dimensional data further reveal the superiority of the proposed algorithm compared with other sketching algorithms for getting low-tubal-rank approximation, in terms of both efficiency and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge