HIT Model: A Hierarchical Interaction-Enhanced Two-Tower Model for Pre-Ranking Systems

Online display advertising platforms rely on pre-ranking systems to efficiently filter and prioritize candidate ads from large corpora, balancing relevance to users with strict computational constraints. The prevailing two-tower architecture, though highly efficient due to its decoupled design and pre-caching, suffers from cross-domain interaction and coarse similarity metrics, undermining its capacity to model complex user-ad relationships. In this study, we propose the Hierarchical Interaction-Enhanced Two-Tower (HIT) model, a new architecture that augments the two-tower paradigm with two key components: $\textit{generators}$ that pre-generate holistic vectors incorporating coarse-grained user-ad interactions through a dual-generator framework with a cosine-similarity-based generation loss as the training objective, and $\textit{multi-head representers}$ that project embeddings into multiple latent subspaces to capture fine-grained, multi-faceted user interests and multi-dimensional ad attributes. This design enhances modeling effectiveness without compromising inference efficiency. Extensive experiments on public datasets and large-scale online A/B testing on Tencent's advertising platform demonstrate that HIT significantly outperforms several baselines in relevance metrics, yielding a $1.66\%$ increase in Gross Merchandise Volume and a $1.55\%$ improvement in Return on Investment, alongside similar serving latency to the vanilla two-tower models. The HIT model has been successfully deployed in Tencent's online display advertising system, serving billions of impressions daily. The code is available at https://anonymous.4open.science/r/HIT_model-5C23.

An interpretable neural network model through piecewise linear approximation

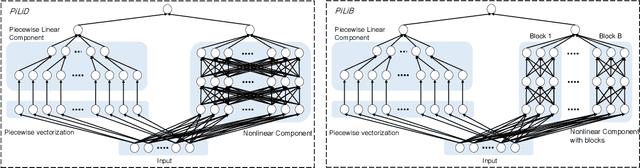
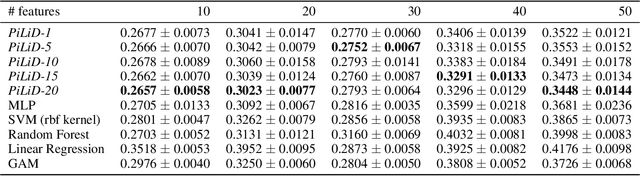
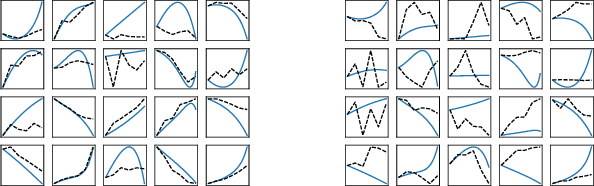
Most existing interpretable methods explain a black-box model in a post-hoc manner, which uses simpler models or data analysis techniques to interpret the predictions after the model is learned. However, they (a) may derive contradictory explanations on the same predictions given different methods and data samples, and (b) focus on using simpler models to provide higher descriptive accuracy at the sacrifice of prediction accuracy. To address these issues, we propose a hybrid interpretable model that combines a piecewise linear component and a nonlinear component. The first component describes the explicit feature contributions by piecewise linear approximation to increase the expressiveness of the model. The other component uses a multi-layer perceptron to capture feature interactions and implicit nonlinearity, and increase the prediction performance. Different from the post-hoc approaches, the interpretability is obtained once the model is learned in the form of feature shapes. We also provide a variant to explore higher-order interactions among features to demonstrate that the proposed model is flexible for adaptation. Experiments demonstrate that the proposed model can achieve good interpretability by describing feature shapes while maintaining state-of-the-art accuracy.

Explainable Ordinal Factorization Model: Deciphering the Effects of Attributes by Piece-wise Linear Approximation

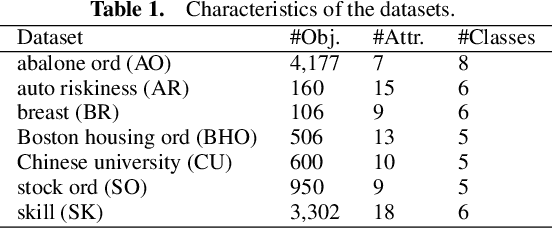
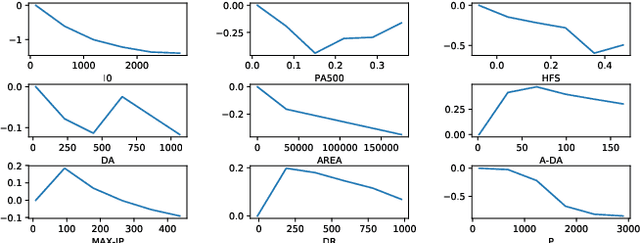
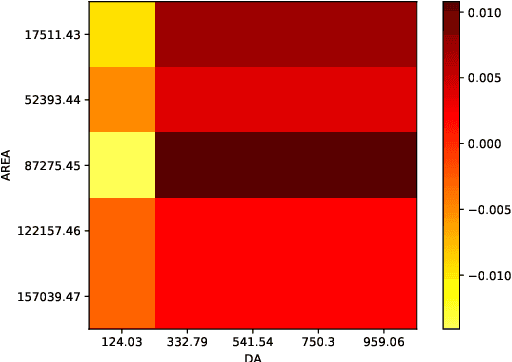
Ordinal regression predicts the objects' labels that exhibit a natural ordering, which is important to many managerial problems such as credit scoring and clinical diagnosis. In these problems, the ability to explain how the attributes affect the prediction is critical to users. However, most, if not all, existing ordinal regression models simplify such explanation in the form of constant coefficients for the main and interaction effects of individual attributes. Such explanation cannot characterize the contributions of attributes at different value scales. To address this challenge, we propose a new explainable ordinal regression model, namely, the Explainable Ordinal Factorization Model (XOFM). XOFM uses the piece-wise linear functions to approximate the actual contributions of individual attributes and their interactions. Moreover, XOFM introduces a novel ordinal transformation process to assign each object the probabilities of belonging to multiple relevant classes, instead of fixing boundaries to differentiate classes. XOFM is based on the Factorization Machines to handle the potential sparsity problem as a result of discretizing the attribute scales. Comprehensive experiments with benchmark datasets and baseline models demonstrate that the proposed XOFM exhibits superior explainability and leads to state-of-the-art prediction accuracy.

An interpretable machine learning framework for modelling human decision behavior

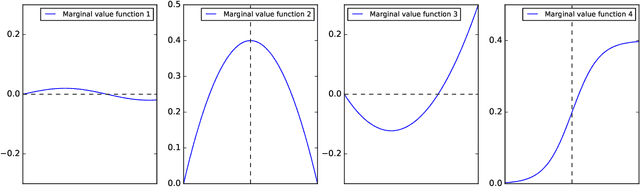
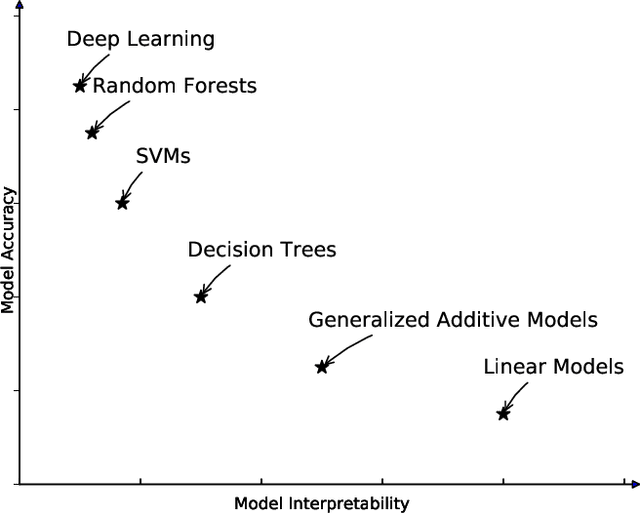
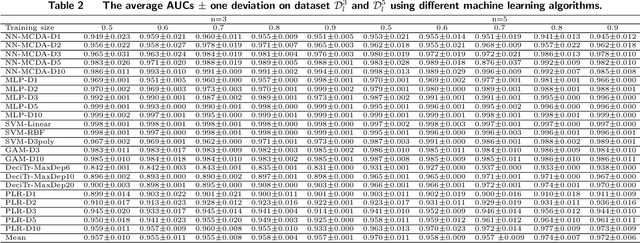
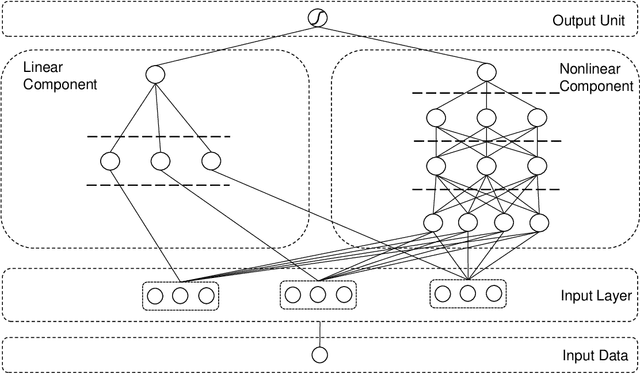
Machine learning has recently been widely adopted to address the managerial decision making problems. However, there is a trade-off between performance and interpretability. Full complexity models (such as neural network-based models) are non-traceable black-box, whereas classic interpretable models (such as logistic regression) are usually simplified with lower accuracy. This trade-off limits the application of state-of-the-art machine learning models in management problems, which requires high prediction performance, as well as the understanding of individual attributes' contributions to the model outcome. Multiple criteria decision aiding (MCDA) is a family of interpretable approaches to depicting the rationale of human decision behavior. It is also limited by strong assumptions (e.g. preference independence). In this paper, we propose an interpretable machine learning approach, namely Neural Network-based Multiple Criteria Decision Aiding (NN-MCDA), which combines an additive MCDA model and a fully-connected multilayer perceptron (MLP) to achieve good performance while preserving a certain degree of interpretability. NN-MCDA has a linear component (in an additive form of a set of polynomial functions) to capture the detailed relationship between individual attributes and the prediction, and a nonlinear component (in a standard MLP form) to capture the high-order interactions between attributes and their complex nonlinear transformations. We demonstrate the effectiveness of NN-MCDA with extensive simulation studies and two real-world datasets. To the best of our knowledge, this research is the first to enhance the interpretability of machine learning models with MCDA techniques. The proposed framework also sheds light on how to use machine learning techniques to free MCDA from strong assumptions.