Generalizing and Unifying Gray-box Combinatorial Optimization Operators

Gray-box optimization leverages the information available about the mathematical structure of an optimization problem to design efficient search operators. Efficient hill climbers and crossover operators have been proposed in the domain of pseudo-Boolean optimization and also in some permutation problems. However, there is no general rule on how to design these efficient operators in different representation domains. This paper proposes a general framework that encompasses all known gray-box operators for combinatorial optimization problems. The framework is general enough to shed light on the design of new efficient operators for new problems and representation domains. We also unify the proofs of efficiency for gray-box hill climbers and crossovers and show that the mathematical property explaining the speed-up of gray-box crossover operators, also explains the efficient identification of improving moves in gray-box hill climbers. We illustrate the power of the new framework by proposing an efficient hill climber and crossover for two related permutation problems: the Linear Ordering Problem and the Single Machine Total Weighted Tardiness Problem.

Large Language Models for the Automated Analysis of Optimization Algorithms

The ability of Large Language Models (LLMs) to generate high-quality text and code has fuelled their rise in popularity. In this paper, we aim to demonstrate the potential of LLMs within the realm of optimization algorithms by integrating them into STNWeb. This is a web-based tool for the generation of Search Trajectory Networks (STNs), which are visualizations of optimization algorithm behavior. Although visualizations produced by STNWeb can be very informative for algorithm designers, they often require a certain level of prior knowledge to be interpreted. In an attempt to bridge this knowledge gap, we have incorporated LLMs, specifically GPT-4, into STNWeb to produce extensive written reports, complemented by automatically generated plots, thereby enhancing the user experience and reducing the barriers to the adoption of this tool by the research community. Moreover, our approach can be expanded to other tools from the optimization community, showcasing the versatility and potential of LLMs in this field.

Dynastic Potential Crossover Operator

An optimal recombination operator for two parent solutions provides the best solution among those that take the value for each variable from one of the parents (gene transmission property). If the solutions are bit strings, the offspring of an optimal recombination operator is optimal in the smallest hyperplane containing the two parent solutions. Exploring this hyperplane is computationally costly, in general, requiring exponential time in the worst case. However, when the variable interaction graph of the objective function is sparse, exploration can be done in polynomial time. In this paper, we present a recombination operator, called Dynastic Potential Crossover (DPX), that runs in polynomial time and behaves like an optimal recombination operator for low-epistasis combinatorial problems. We compare this operator, both theoretically and experimentally, with traditional crossover operators, like uniform crossover and network crossover, and with two recently defined efficient recombination operators: partition crossover and articulation points partition crossover. The empirical comparison uses NKQ Landscapes and MAX-SAT instances. DPX outperforms the other crossover operators in terms of quality of the offspring and provides better results included in a trajectory and a population-based metaheuristic, but it requires more time and memory to compute the offspring.

Multiobjective Evolutionary Component Effect on Algorithm behavior

The performance of multiobjective evolutionary algorithms (MOEAs) varies across problems, making it hard to develop new algorithms or apply existing ones to new problems. To simplify the development and application of new multiobjective algorithms, there has been an increasing interest in their automatic design from their components. These automatically designed metaheuristics can outperform their human-developed counterparts. However, it is still unknown what are the most influential components that lead to performance improvements. This study specifies a new methodology to investigate the effects of the final configuration of an automatically designed algorithm. We apply this methodology to a tuned Multiobjective Evolutionary Algorithm based on Decomposition (MOEA/D) designed by the iterated racing (irace) configuration package on constrained problems of 3 groups: (1) analytical real-world problems, (2) analytical artificial problems and (3) simulated real-world. We then compare the impact of the algorithm components in terms of their Search Trajectory Networks (STNs), the diversity of the population, and the anytime hypervolume values. Looking at the objective space behavior, the MOEAs studied converged before half of the search to generally good HV values in the analytical artificial problems and the analytical real-world problems. For the simulated problems, the HV values are still improving at the end of the run. In terms of decision space behavior, we see a diverse set of the trajectories of the STNs in the analytical artificial problems. These trajectories are more similar and frequently reach optimal solutions in the other problems.

Phenotype Search Trajectory Networks for Linear Genetic Programming

Genotype-to-phenotype mappings translate genotypic variations such as mutations into phenotypic changes. Neutrality is the observation that some mutations do not lead to phenotypic changes. Studying the search trajectories in genotypic and phenotypic spaces, especially through neutral mutations, helps us to better understand the progression of evolution and its algorithmic behaviour. In this study, we visualise the search trajectories of a genetic programming system as graph-based models, where nodes are genotypes/phenotypes and edges represent their mutational transitions. We also quantitatively measure the characteristics of phenotypes including their genotypic abundance (the requirement for neutrality) and Kolmogorov complexity. We connect these quantified metrics with search trajectory visualisations, and find that more complex phenotypes are under-represented by fewer genotypes and are harder for evolution to discover. Less complex phenotypes, on the other hand, are over-represented by genotypes, are easier to find, and frequently serve as stepping-stones for evolution.

Component-wise Analysis of Automatically Designed Multiobjective Algorithms on Constrained Problems

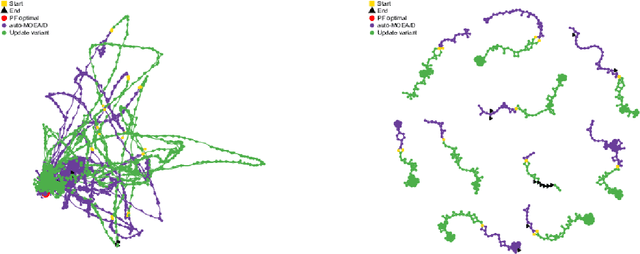
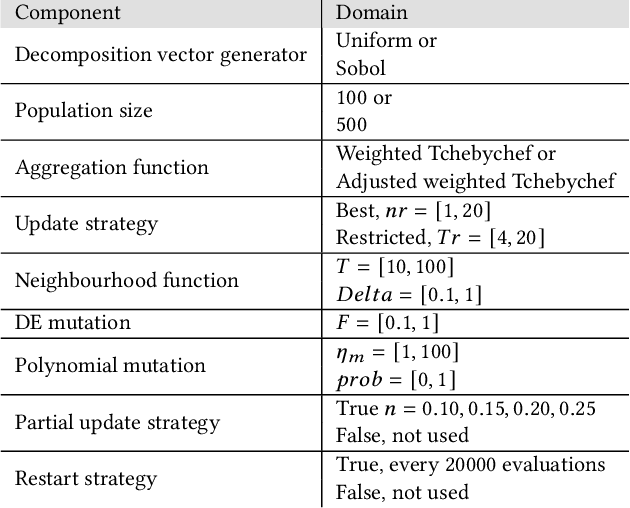
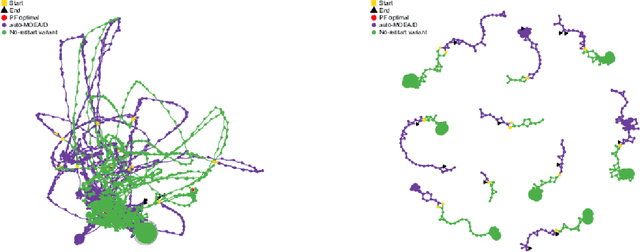
The performance of multiobjective algorithms varies across problems, making it hard to develop new algorithms or apply existing ones to new problems. To simplify the development and application of new multiobjective algorithms, there has been an increasing interest in their automatic design from component parts. These automatically designed metaheuristics can outperform their human-developed counterparts. However, it is still uncertain what are the most influential components leading to their performance improvement. This study introduces a new methodology to investigate the effects of the final configuration of an automatically designed algorithm. We apply this methodology to a well-performing Multiobjective Evolutionary Algorithm Based on Decomposition (MOEA/D) designed by the irace package on nine constrained problems. We then contrast the impact of the algorithm components in terms of their Search Trajectory Networks (STNs), the diversity of the population, and the hypervolume. Our results indicate that the most influential components were the restart and update strategies, with higher increments in performance and more distinct metric values. Also, their relative influence depends on the problem difficulty: not using the restart strategy was more influential in problems where MOEA/D performs better; while the update strategy was more influential in problems where MOEA/D performs the worst.

Search Trajectories Networks of Multiobjective Evolutionary Algorithms

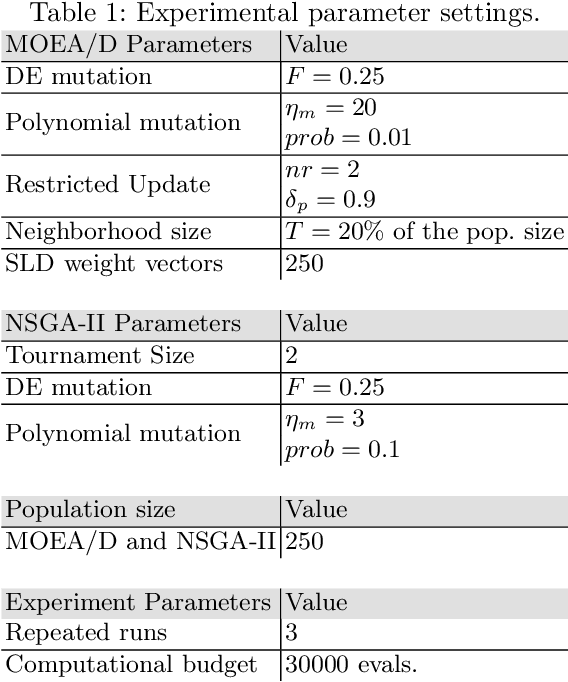
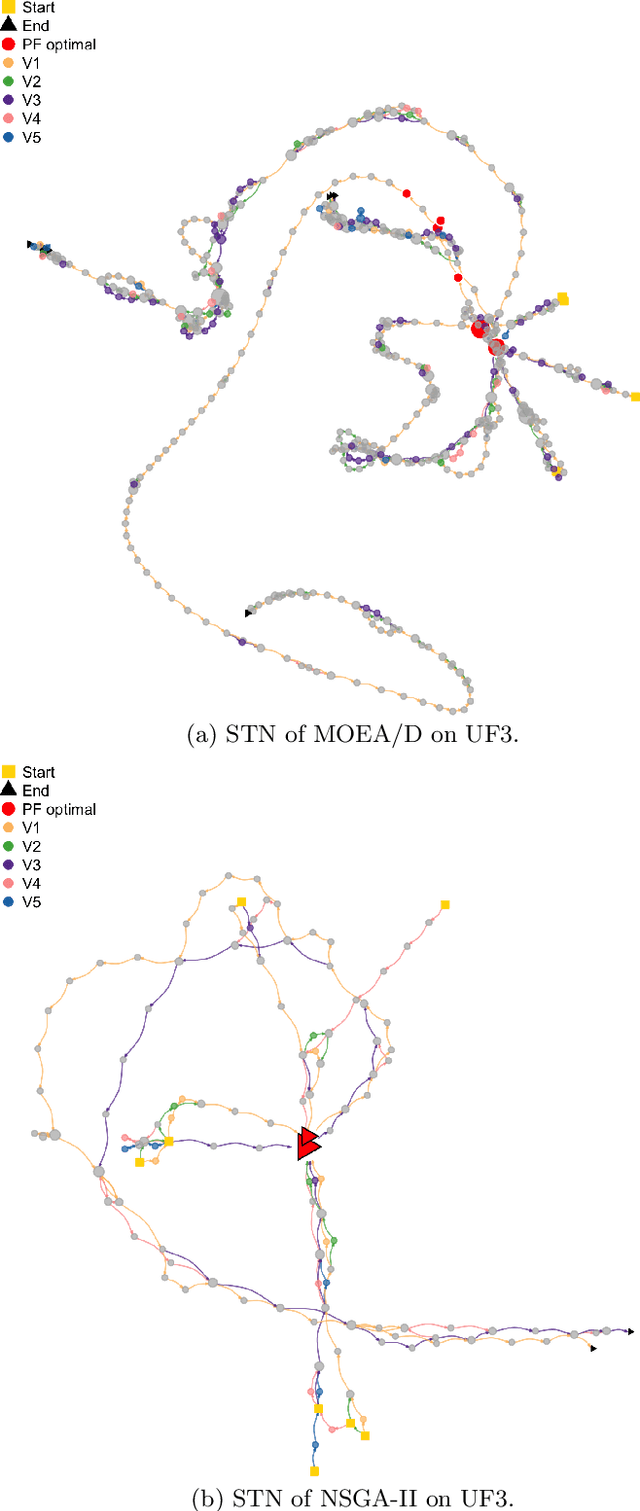
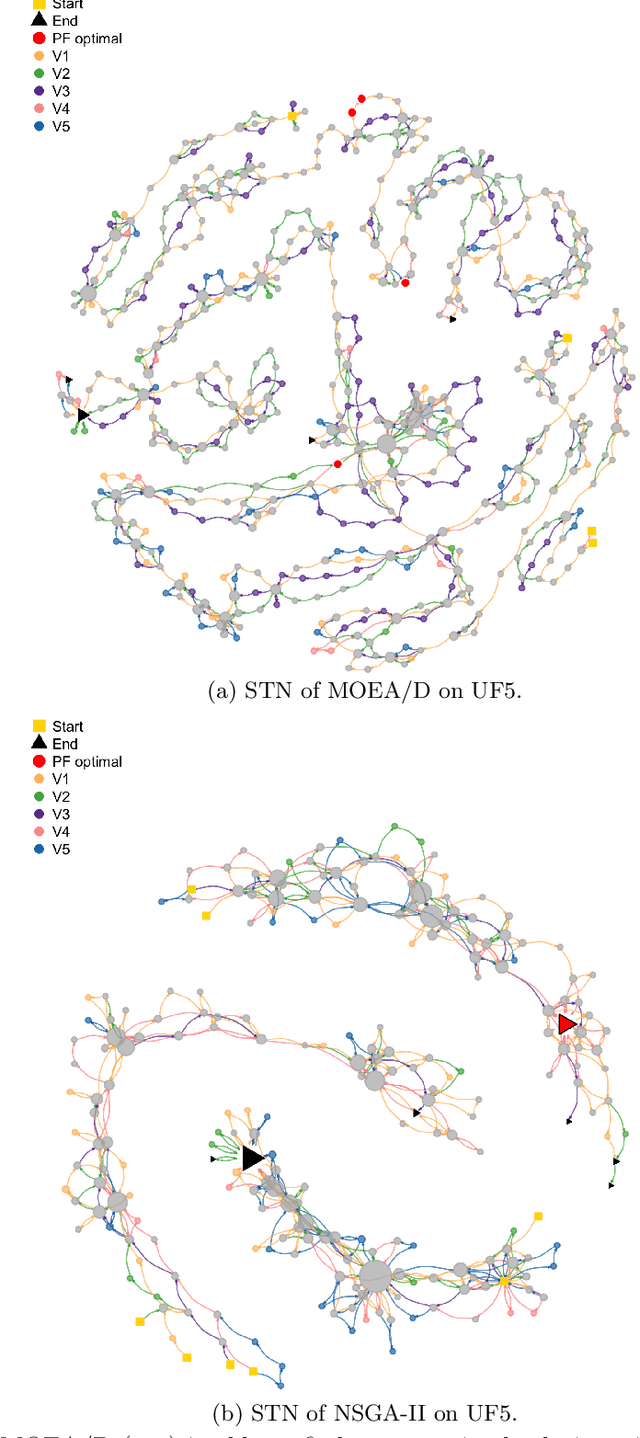
Understanding the search dynamics of multiobjective evolutionary algorithms (MOEAs) is still an open problem. This paper extends a recent network-based tool, search trajectory networks (STNs), to model the behavior of MOEAs. Our approach uses the idea of decomposition, where a multiobjective problem is transformed into several single-objective problems. We show that STNs can be used to model and distinguish the search behavior of two popular multiobjective algorithms, MOEA/D and NSGA-II, using 10 continuous benchmark problems with 2 and 3 objectives. Our findings suggest that we can improve our understanding of MOEAs using STNs for algorithm analysis.

Local Optima Networks: A New Model of Combinatorial Fitness Landscapes

This chapter overviews a recently introduced network-based model of combinatorial landscapes: Local Optima Networks (LON). The model compresses the information given by the whole search space into a smaller mathematical object that is a graph having as vertices the local optima and as edges the possible weighted transitions between them. Two definitions of edges have been proposed: basin-transition and escape-edges, which capture relevant topological features of the underlying search spaces. This network model brings a new set of metrics to characterize the structure of combinatorial landscapes, those associated with the science of complex networks. These metrics are described, and results are presented of local optima network extraction and analysis for two selected combinatorial landscapes: NK landscapes and the quadratic assignment problem. Network features are found to correlate with and even predict the performance of heuristic search algorithms operating on these problems.

Local Optima Networks, Landscape Autocorrelation and Heuristic Search Performance

Recent developments in fitness landscape analysis include the study of Local Optima Networks (LON) and applications of the Elementary Landscapes theory. This paper represents a first step at combining these two tools to explore their ability to forecast the performance of search algorithms. We base our analysis on the Quadratic Assignment Problem (QAP) and conduct a large statistical study over 600 generated instances of different types. Our results reveal interesting links between the network measures, the autocorrelation measures and the performance of heuristic search algorithms.

Local optima networks and the performance of iterated local search

Local Optima Networks (LONs) have been recently proposed as an alternative model of combinatorial fitness landscapes. The model compresses the information given by the whole search space into a smaller mathematical object that is the graph having as vertices the local optima and as edges the possible weighted transitions between them. A new set of metrics can be derived from this model that capture the distribution and connectivity of the local optima in the underlying configuration space. This paper departs from the descriptive analysis of local optima networks, and actively studies the correlation between network features and the performance of a local search heuristic. The NK family of landscapes and the Iterated Local Search metaheuristic are considered. With a statistically-sound approach based on multiple linear regression, it is shown that some LONs' features strongly influence and can even partly predict the performance of a heuristic search algorithm. This study validates the expressive power of LONs as a model of combinatorial fitness landscapes.