AbCD: A Component-wise Adjustable Framework for Dynamic Optimization Problems

Dynamic Optimization Problems (DOPs) are characterized by changes in the fitness landscape that can occur at any time and are common in real world applications. The main issues to be considered include detecting the change in the fitness landscape and reacting in accord. Over the years, several evolutionary algorithms have been proposed to take into account this characteristic during the optimization process. However, the number of available tools or open source codebases for these approaches is limited, making reproducibility and extensive experimentation difficult. To solve this, we developed a component-oriented framework for DOPs called Adjustable Components for Dynamic Problems (AbCD), inspired by similar works in the Multiobjective static domain. Using this framework, we investigate components that were proposed in several popular DOP algorithms. Our experiments show that the performance of these components depends on the problem and the selected components used in a configuration, which differs from the results reported in the literature. Using irace, we demonstrate how this framework can automatically generate DOP algorithm configurations that take into account the characteristics of the problem to be solved. Our results highlight existing problems in the DOP field that need to be addressed in the future development of algorithms and components.

Multiobjective Evolutionary Component Effect on Algorithm behavior

The performance of multiobjective evolutionary algorithms (MOEAs) varies across problems, making it hard to develop new algorithms or apply existing ones to new problems. To simplify the development and application of new multiobjective algorithms, there has been an increasing interest in their automatic design from their components. These automatically designed metaheuristics can outperform their human-developed counterparts. However, it is still unknown what are the most influential components that lead to performance improvements. This study specifies a new methodology to investigate the effects of the final configuration of an automatically designed algorithm. We apply this methodology to a tuned Multiobjective Evolutionary Algorithm based on Decomposition (MOEA/D) designed by the iterated racing (irace) configuration package on constrained problems of 3 groups: (1) analytical real-world problems, (2) analytical artificial problems and (3) simulated real-world. We then compare the impact of the algorithm components in terms of their Search Trajectory Networks (STNs), the diversity of the population, and the anytime hypervolume values. Looking at the objective space behavior, the MOEAs studied converged before half of the search to generally good HV values in the analytical artificial problems and the analytical real-world problems. For the simulated problems, the HV values are still improving at the end of the run. In terms of decision space behavior, we see a diverse set of the trajectories of the STNs in the analytical artificial problems. These trajectories are more similar and frequently reach optimal solutions in the other problems.

Component-wise Analysis of Automatically Designed Multiobjective Algorithms on Constrained Problems

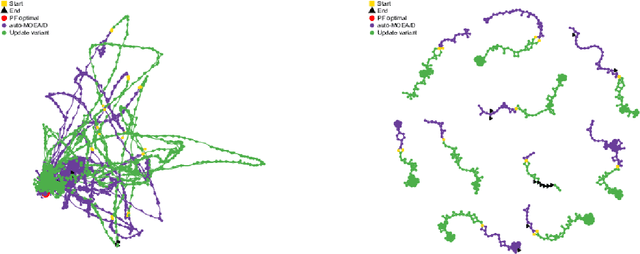
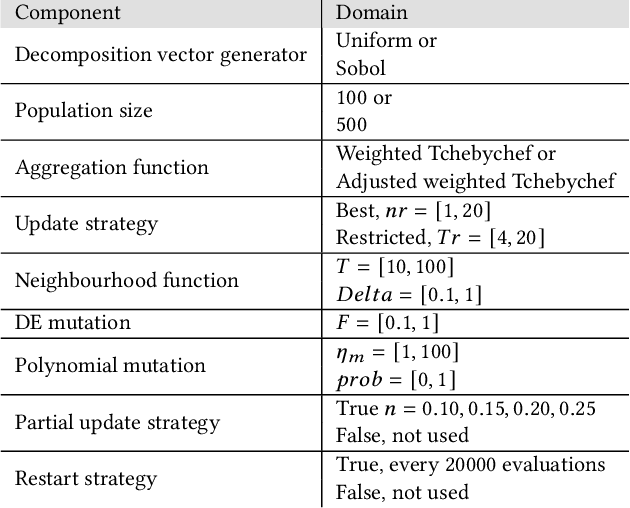
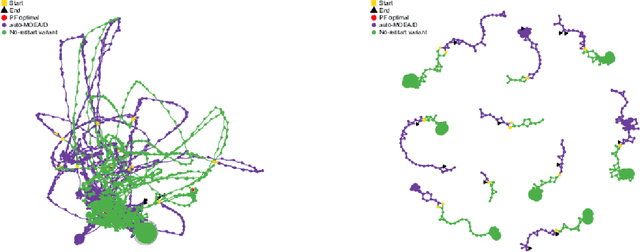
The performance of multiobjective algorithms varies across problems, making it hard to develop new algorithms or apply existing ones to new problems. To simplify the development and application of new multiobjective algorithms, there has been an increasing interest in their automatic design from component parts. These automatically designed metaheuristics can outperform their human-developed counterparts. However, it is still uncertain what are the most influential components leading to their performance improvement. This study introduces a new methodology to investigate the effects of the final configuration of an automatically designed algorithm. We apply this methodology to a well-performing Multiobjective Evolutionary Algorithm Based on Decomposition (MOEA/D) designed by the irace package on nine constrained problems. We then contrast the impact of the algorithm components in terms of their Search Trajectory Networks (STNs), the diversity of the population, and the hypervolume. Our results indicate that the most influential components were the restart and update strategies, with higher increments in performance and more distinct metric values. Also, their relative influence depends on the problem difficulty: not using the restart strategy was more influential in problems where MOEA/D performs better; while the update strategy was more influential in problems where MOEA/D performs the worst.

Search Trajectories Networks of Multiobjective Evolutionary Algorithms

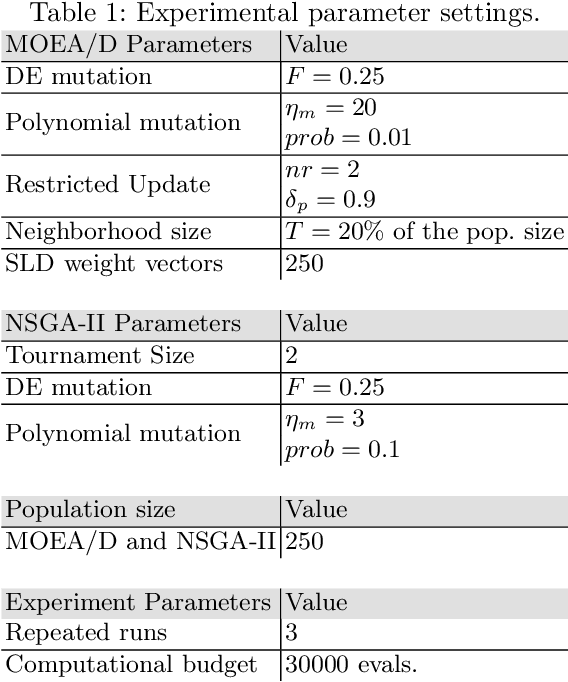
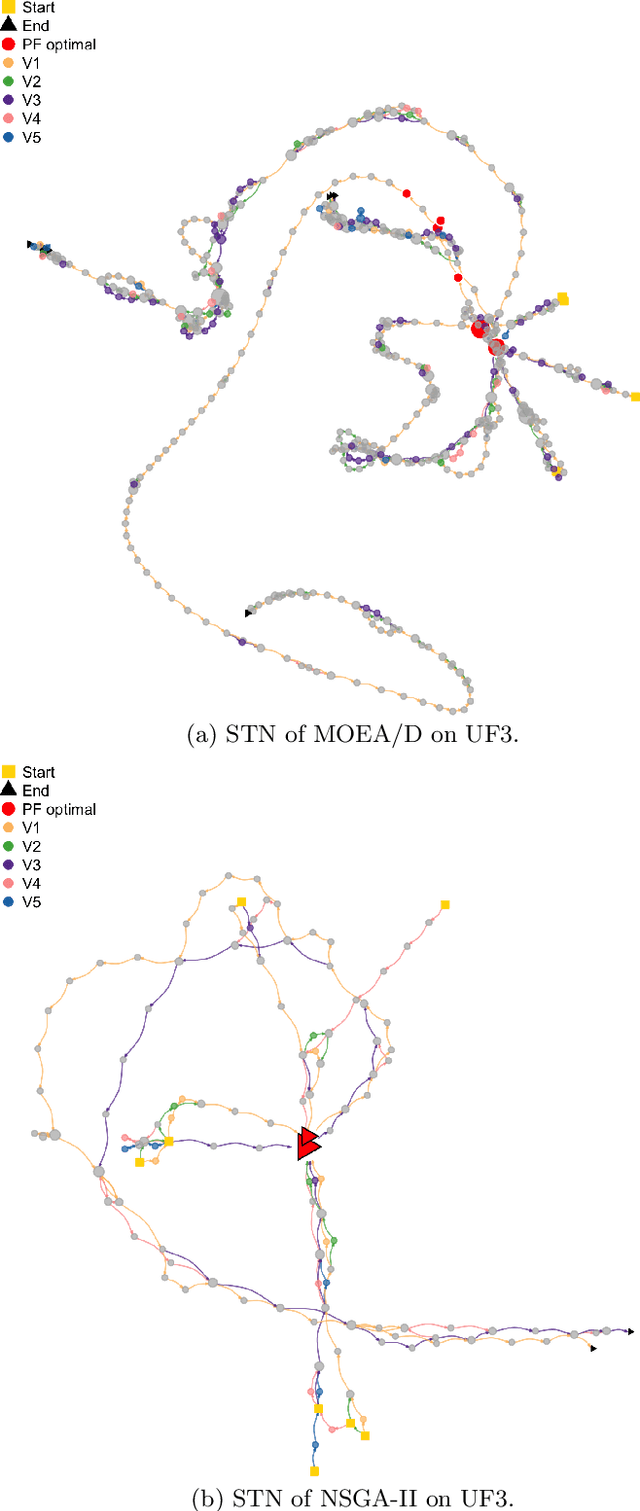
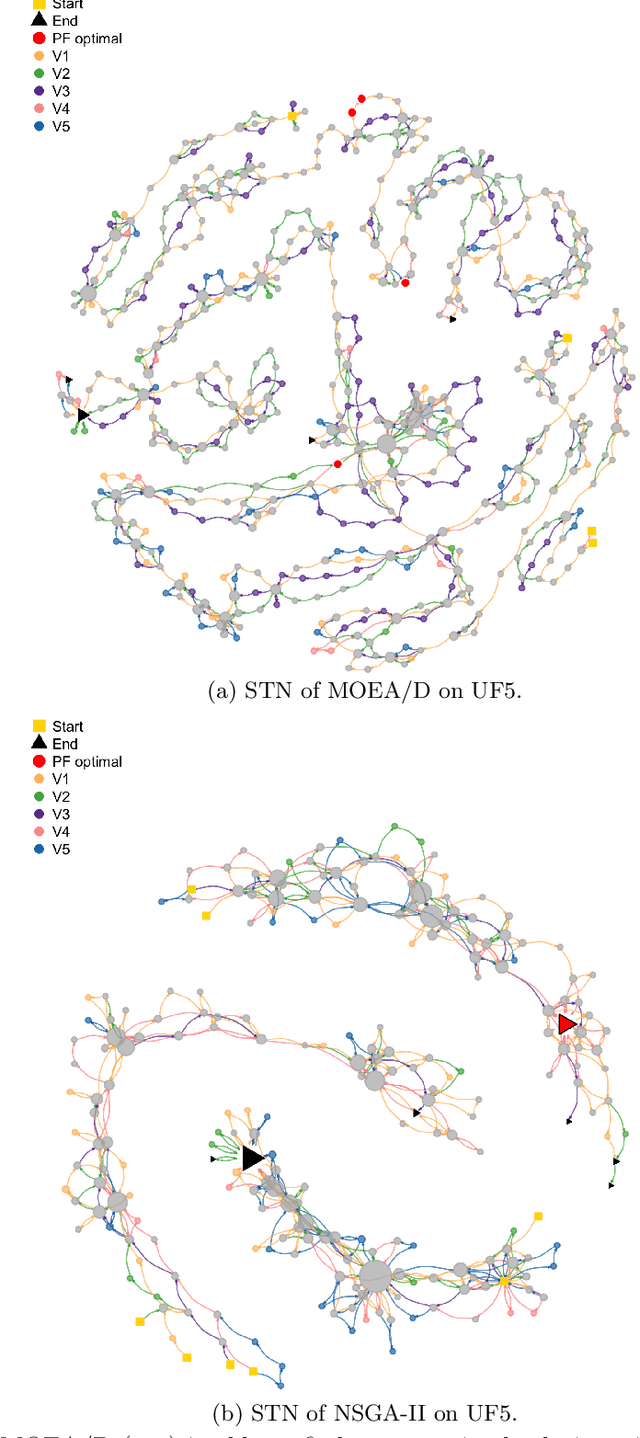
Understanding the search dynamics of multiobjective evolutionary algorithms (MOEAs) is still an open problem. This paper extends a recent network-based tool, search trajectory networks (STNs), to model the behavior of MOEAs. Our approach uses the idea of decomposition, where a multiobjective problem is transformed into several single-objective problems. We show that STNs can be used to model and distinguish the search behavior of two popular multiobjective algorithms, MOEA/D and NSGA-II, using 10 continuous benchmark problems with 2 and 3 objectives. Our findings suggest that we can improve our understanding of MOEAs using STNs for algorithm analysis.

Faster Convergence in Multi-Objective Optimization Algorithms Based on Decomposition

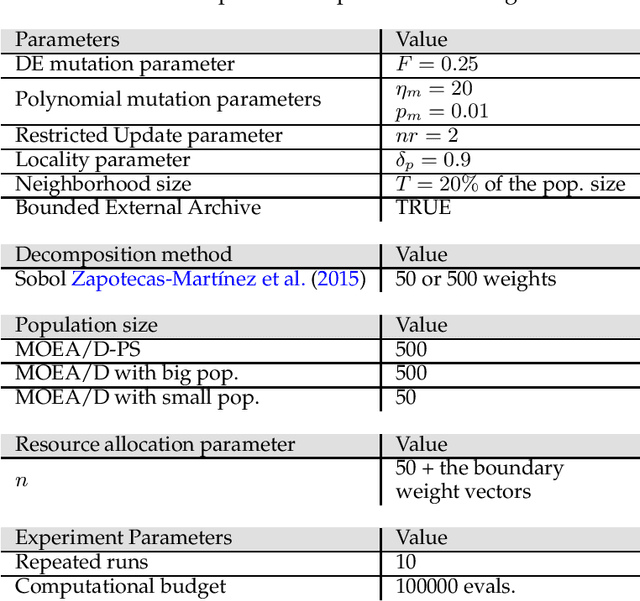
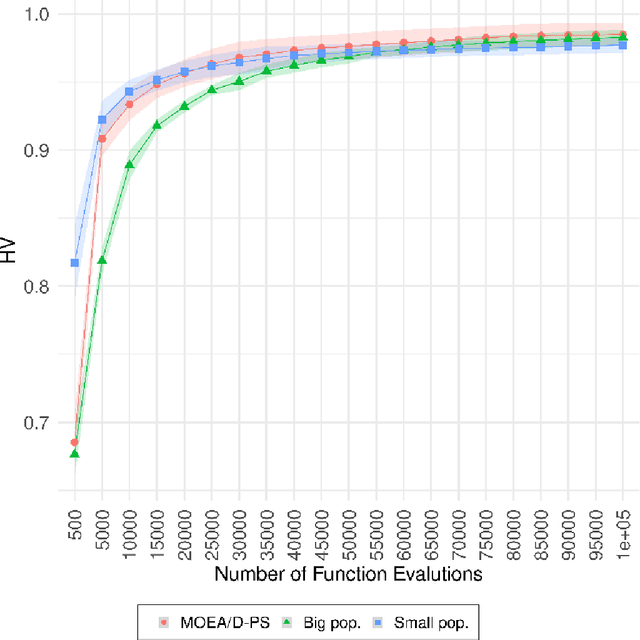
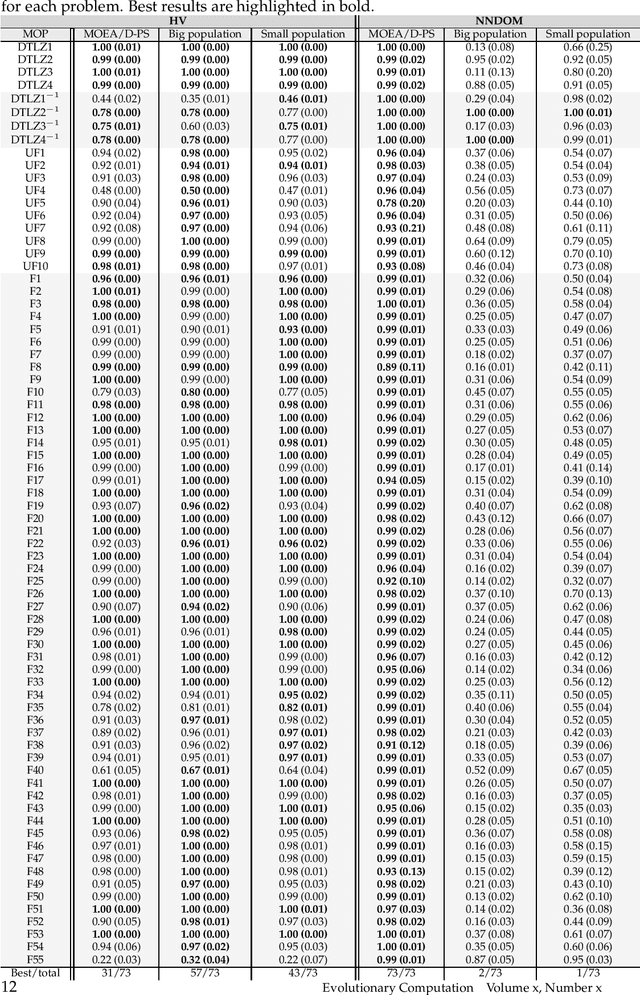
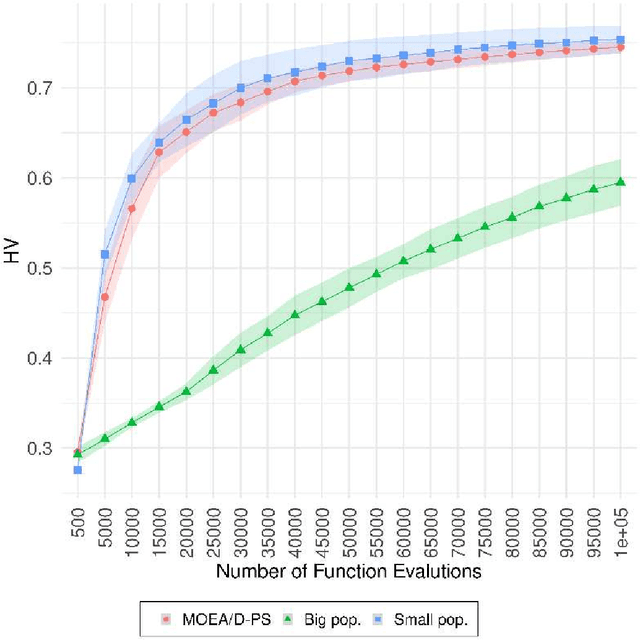
The Resource Allocation approach (RA) improves the performance of MOEA/D by maintaining a big population and updating few solutions each generation. However, most of the studies on RA generally focused on the properties of different Resource Allocation metrics. Thus, it is still uncertain what the main factors are that lead to increments in performance of MOEA/D with RA. This study investigates the effects of MOEA/D with the Partial Update Strategy in an extensive set of MOPs to generate insights into correspondences of MOEA/D with the Partial Update and MOEA/D with small population size and big population size. Our work undertakes an in-depth analysis of the populational dynamics behaviour considering their final approximation Pareto sets, anytime hypervolume performance, attained regions and number of unique non-dominated solutions. Our results indicate that MOEA/D with Partial Update progresses with the search as fast as MOEA/D with small population size and explores the search space as MOEA/D with big population size. MOEA/D with Partial Update can mitigate common problems related to population size choice with better convergence speed in most MOPs, as shown by the results of hypervolume and number of unique non-dominated solutions, the anytime performance and Empirical Attainment Function indicates.

MOEA/D with Adaptative Number of Weight Vectors

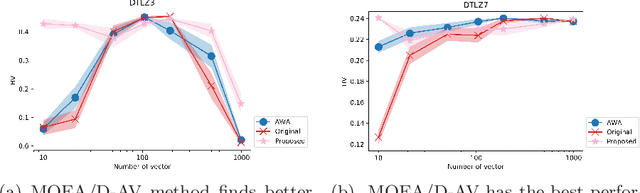
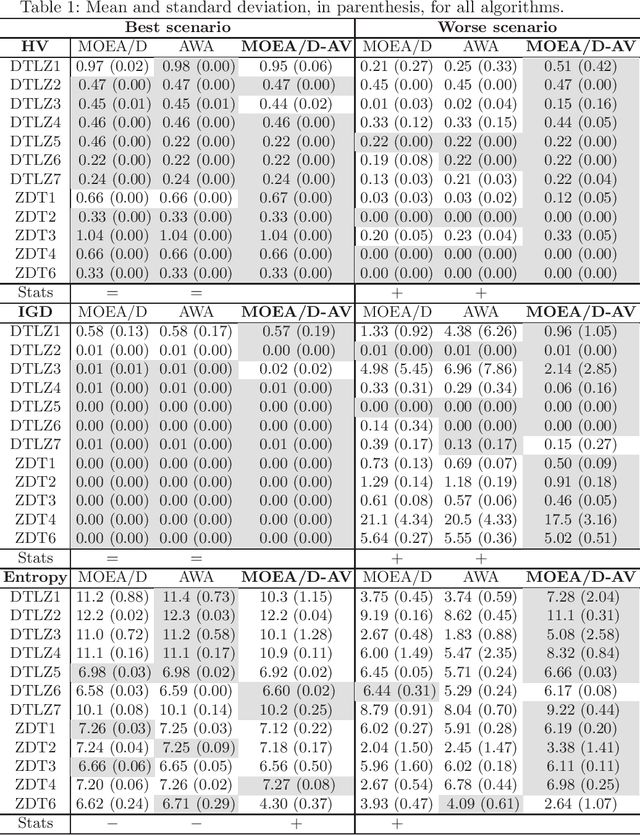
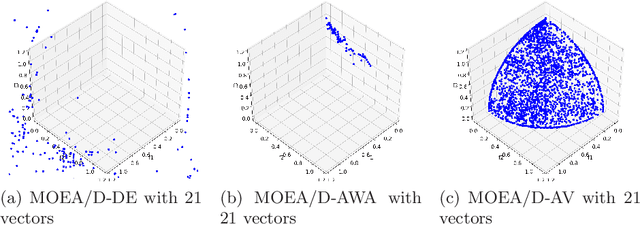
The Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) is a popular algorithm for solving Multi-Objective Problems (MOPs). The main component of MOEA/D is to decompose a MOP into easier sub-problems using a set of weight vectors. The choice of the number of weight vectors significantly impacts the performance of MOEA/D. However, the right choice for this number varies, given different MOPs and search stages. Here we adaptively change the number of vectors by removing unnecessary vectors and adding new ones in empty areas of the objective space. Our MOEA/D variant uses the Consolidation Ratio to decide when to change the number of vectors, and then it decides where to add or remove these weighted vectors. We investigate the effects of this adaptive MOEA/D against MOEA/D with a poorly chosen set of vectors, a MOEA/D with fine-tuned vectors and MOEA/D-AWA on the DTLZ and ZDT benchmark functions. We analyse the algorithms in terms of hypervolume, IGD and entropy performance. Our results show that the proposed method is equivalent to MOEA/D with fine-tuned vectors and superior to MOEA/D with poorly defined vectors. Thus, our adaptive mechanism mitigates problems related to the choice of the number of weight vectors in MOEA/D, increasing the final performance of MOEA/D by filling empty areas of the objective space while avoiding premature stagnation of the search progress.

Exploring Constraint Handling Techniques in Real-world Problems on MOEA/D with Limited Budget of Evaluations

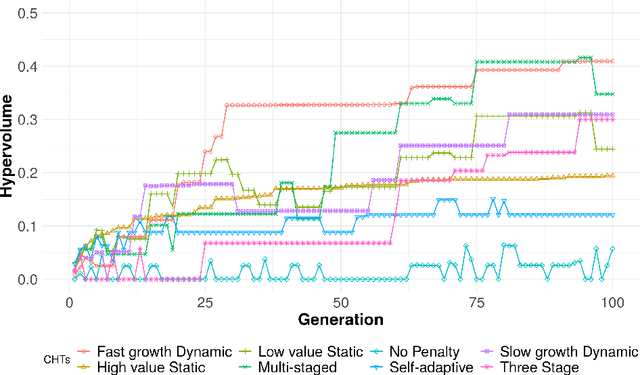
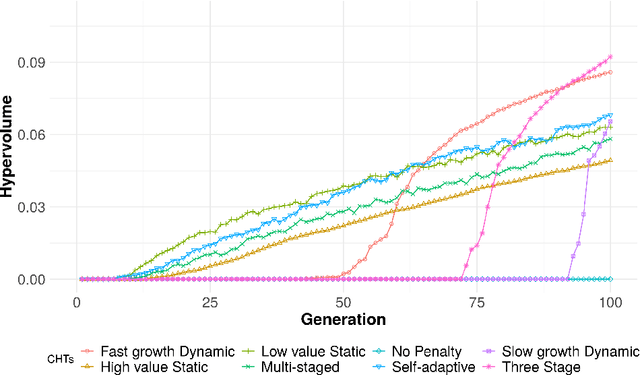
Finding good solutions for Multi-objective Optimization (MOPs) Problems is considered a hard problem, especially when considering MOPs with constraints. Thus, most of the works in the context of MOPs do not explore in-depth how different constraints affect the performance of MOP solvers. Here, we focus on exploring the effects of different Constraint Handling Techniques (CHTs) on MOEA/D, a commonly used MOP solver when solving complex real-world MOPs. Moreover, we introduce a simple and effective CHT focusing on the exploration of the decision space, the Three Stage Penalty. We explore each of these CHTs in MOEA/D on two simulated MOPs and six analytic MOPs (eight in total). The results of this work indicate that while the best CHT is problem-dependent, our new proposed Three Stage Penalty achieves competitive results and remarkable performance in terms of hypervolume values in the hard simulated car design MOP.

MOEA/D with Random Partial Update Strategy

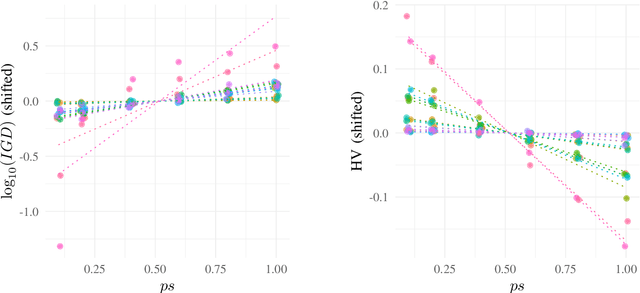
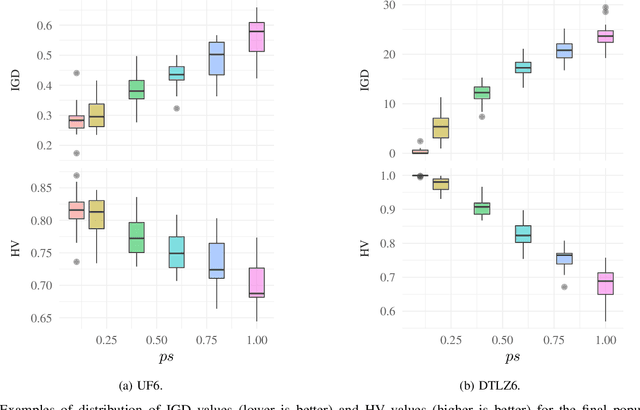
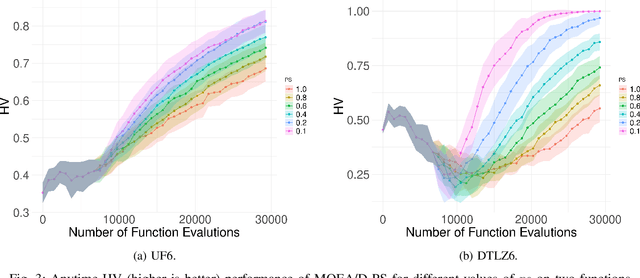
Recent studies on resource allocation suggest that some subproblems are more important than others in the context of the MOEA/D, and that focusing on the most relevant ones can consistently improve the performance of that algorithm. These studies share the common characteristic of updating only a fraction of the population at any given iteration of the algorithm. In this work we investigate a new, simpler partial update strategy, in which a random subset of solutions is selected at every iteration. The performance of the MOEA/D using this new resource allocation approach is compared experimentally against that of the standard MOEA/D-DE and the MOEA/D with relative improvement-based resource allocation. The results indicate that using the MOEA/D with this new partial update strategy results in improved HV and IGD values, and a much higher proportion of non-dominated solutions, particularly as the number of updated solutions at every iteration is reduced.