Geovani Rizk
ByzFL: Research Framework for Robust Federated Learning
May 30, 2025Abstract:We present ByzFL, an open-source Python library for developing and benchmarking robust federated learning (FL) algorithms. ByzFL provides a unified and extensible framework that includes implementations of state-of-the-art robust aggregators, a suite of configurable attacks, and tools for simulating a variety of FL scenarios, including heterogeneous data distributions, multiple training algorithms, and adversarial threat models. The library enables systematic experimentation via a single JSON-based configuration file and includes built-in utilities for result visualization. Compatible with PyTorch tensors and NumPy arrays, ByzFL is designed to facilitate reproducible research and rapid prototyping of robust FL solutions. ByzFL is available at https://byzfl.epfl.ch/, with source code hosted on GitHub: https://github.com/LPD-EPFL/byzfl.
Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants
Aug 07, 2024
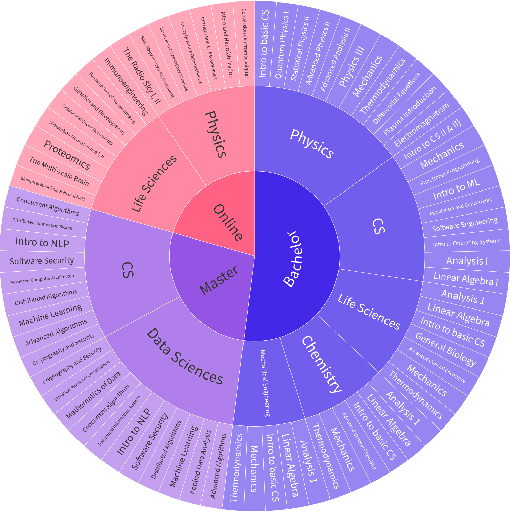
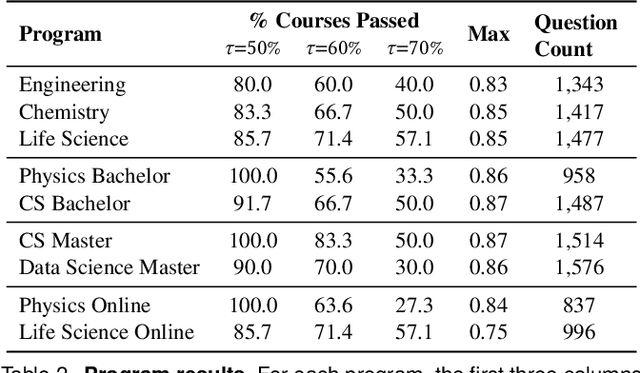

Abstract:AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.
Boosting Robustness by Clipping Gradients in Distributed Learning
May 23, 2024



Abstract:Robust distributed learning consists in achieving good learning performance despite the presence of misbehaving workers. State-of-the-art (SOTA) robust distributed gradient descent (Robust-DGD) methods, relying on robust aggregation, have been proven to be optimal: Their learning error matches the lower bound established under the standard heterogeneity model of $(G, B)$-gradient dissimilarity. The learning guarantee of SOTA Robust-DGD cannot be further improved when model initialization is done arbitrarily. However, we show that it is possible to circumvent the lower bound, and improve the learning performance, when the workers' gradients at model initialization are assumed to be bounded. We prove this by proposing pre-aggregation clipping of workers' gradients, using a novel scheme called adaptive robust clipping (ARC). Incorporating ARC in Robust-DGD provably improves the learning, under the aforementioned assumption on model initialization. The factor of improvement is prominent when the tolerable fraction of misbehaving workers approaches the breakdown point. ARC induces this improvement by constricting the search space, while preserving the robustness property of the original aggregation scheme at the same time. We validate this theoretical finding through exhaustive experiments on benchmark image classification tasks.
Overcoming the Challenges of Batch Normalization in Federated Learning
May 23, 2024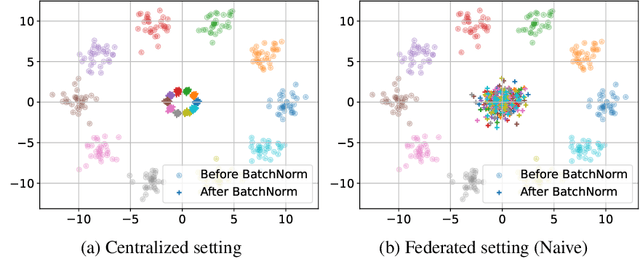
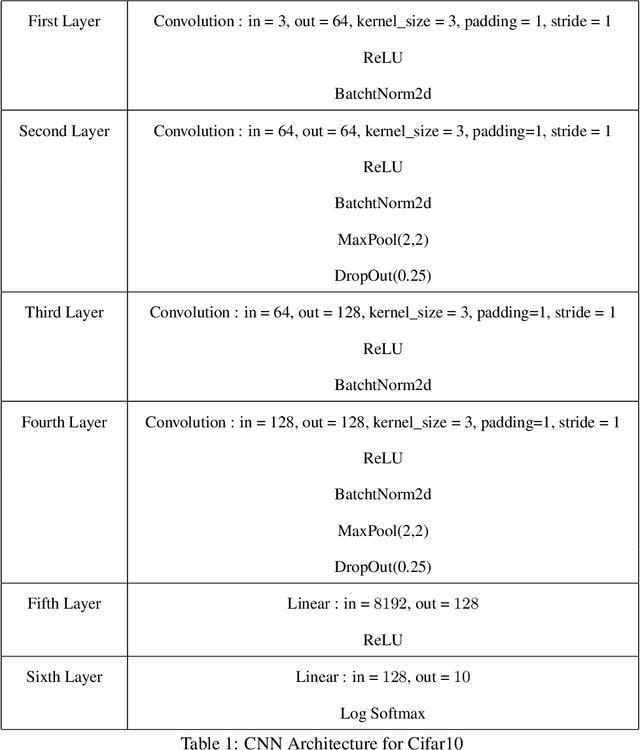
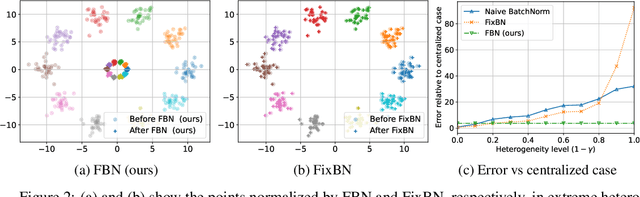
Abstract:Batch normalization has proven to be a very beneficial mechanism to accelerate the training and improve the accuracy of deep neural networks in centralized environments. Yet, the scheme faces significant challenges in federated learning, especially under high data heterogeneity. Essentially, the main challenges arise from external covariate shifts and inconsistent statistics across clients. We introduce in this paper Federated BatchNorm (FBN), a novel scheme that restores the benefits of batch normalization in federated learning. Essentially, FBN ensures that the batch normalization during training is consistent with what would be achieved in a centralized execution, hence preserving the distribution of the data, and providing running statistics that accurately approximate the global statistics. FBN thereby reduces the external covariate shift and matches the evaluation performance of the centralized setting. We also show that, with a slight increase in complexity, we can robustify FBN to mitigate erroneous statistics and potentially adversarial attacks.
Tackling Byzantine Clients in Federated Learning
Feb 20, 2024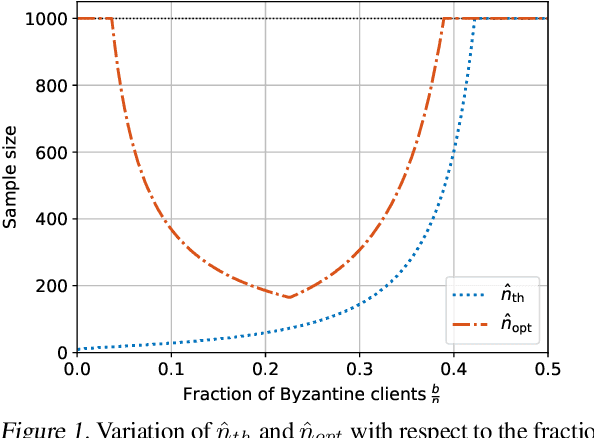
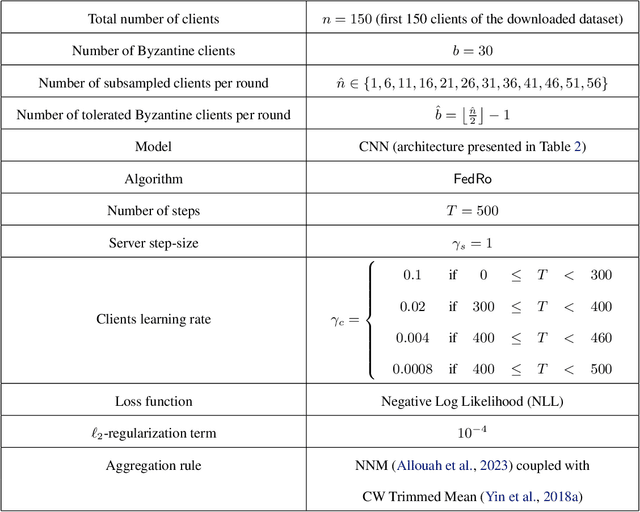
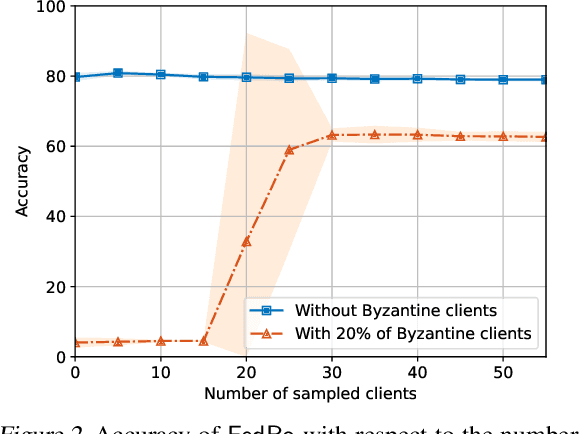
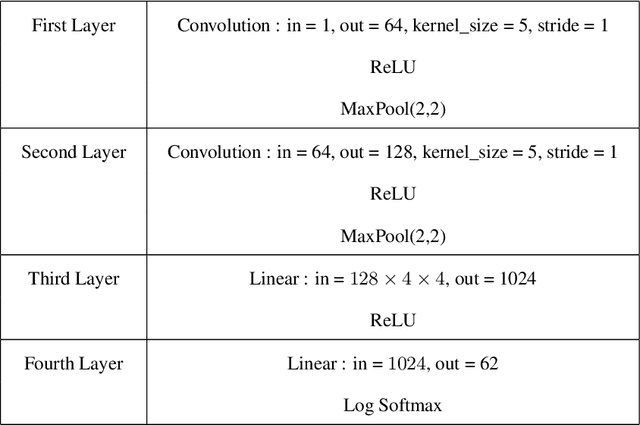
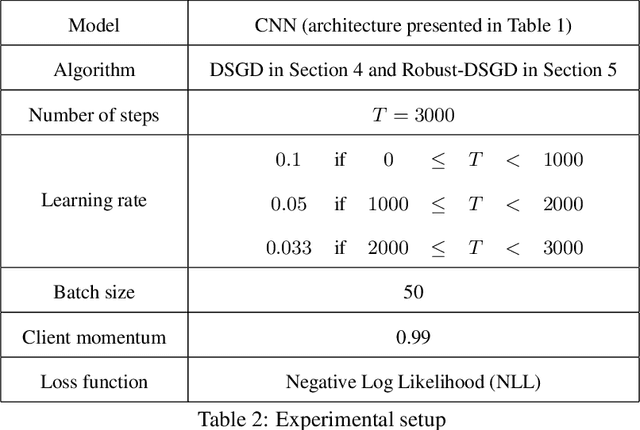
Abstract:The possibility of adversarial (a.k.a., {\em Byzantine}) clients makes federated learning (FL) prone to arbitrary manipulation. The natural approach to robustify FL against adversarial clients is to replace the simple averaging operation at the server in the standard $\mathsf{FedAvg}$ algorithm by a \emph{robust averaging rule}. While a significant amount of work has been devoted to studying the convergence of federated {\em robust averaging} (which we denote by $\mathsf{FedRo}$), prior work has largely ignored the impact of {\em client subsampling} and {\em local steps}, two fundamental FL characteristics. While client subsampling increases the effective fraction of Byzantine clients, local steps increase the drift between the local updates computed by honest (i.e., non-Byzantine) clients. Consequently, a careless deployment of $\mathsf{FedRo}$ could yield poor performance. We validate this observation by presenting an in-depth analysis of $\mathsf{FedRo}$ tightly analyzing the impact of client subsampling and local steps. Specifically, we present a sufficient condition on client subsampling for nearly-optimal convergence of $\mathsf{FedRo}$ (for smooth non-convex loss). Also, we show that the rate of improvement in learning accuracy {\em diminishes} with respect to the number of clients subsampled, as soon as the sample size exceeds a threshold value. Interestingly, we also observe that under a careful choice of step-sizes, the learning error due to Byzantine clients decreases with the number of local steps. We validate our theory by experiments on the FEMNIST and CIFAR-$10$ image classification tasks.
Robust Distributed Learning: Tight Error Bounds and Breakdown Point under Data Heterogeneity
Sep 24, 2023Abstract:The theory underlying robust distributed learning algorithms, designed to resist adversarial machines, matches empirical observations when data is homogeneous. Under data heterogeneity however, which is the norm in practical scenarios, established lower bounds on the learning error are essentially vacuous and greatly mismatch empirical observations. This is because the heterogeneity model considered is too restrictive and does not cover basic learning tasks such as least-squares regression. We consider in this paper a more realistic heterogeneity model, namely (G,B)-gradient dissimilarity, and show that it covers a larger class of learning problems than existing theory. Notably, we show that the breakdown point under heterogeneity is lower than the classical fraction 1/2. We also prove a new lower bound on the learning error of any distributed learning algorithm. We derive a matching upper bound for a robust variant of distributed gradient descent, and empirically show that our analysis reduces the gap between theory and practice.
An $α$-No-Regret Algorithm For Graphical Bilinear Bandits
Jun 01, 2022
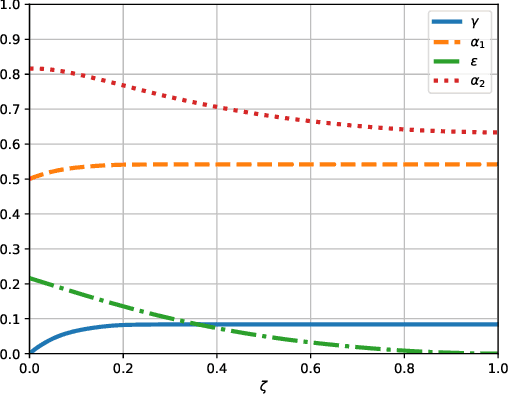
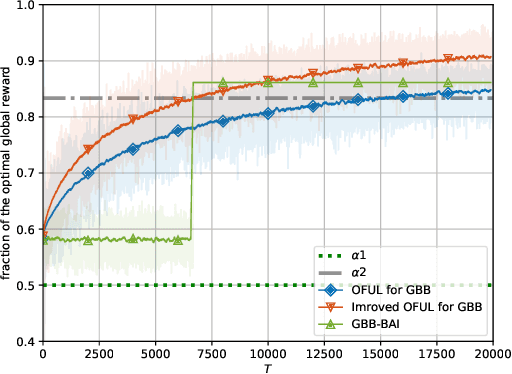
Abstract:We propose the first regret-based approach to the Graphical Bilinear Bandits problem, where $n$ agents in a graph play a stochastic bilinear bandit game with each of their neighbors. This setting reveals a combinatorial NP-hard problem that prevents the use of any existing regret-based algorithm in the (bi-)linear bandit literature. In this paper, we fill this gap and present the first regret-based algorithm for graphical bilinear bandits using the principle of optimism in the face of uncertainty. Theoretical analysis of this new method yields an upper bound of $\tilde{O}(\sqrt{T})$ on the $\alpha$-regret and evidences the impact of the graph structure on the rate of convergence. Finally, we show through various experiments the validity of our approach.
Refined bounds for randomized experimental design
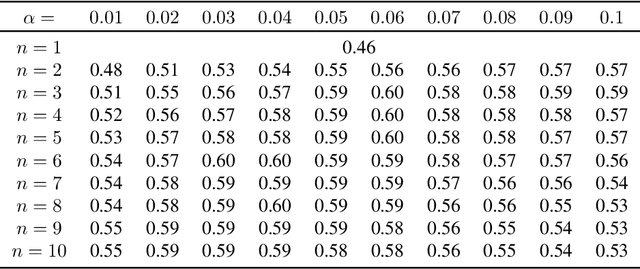
Dec 22, 2020Abstract:Experimental design is an approach for selecting samples among a given set so as to obtain the best estimator for a given criterion. In the context of linear regression, several optimal designs have been derived, each associated with a different criterion: mean square error, robustness, \emph{etc}. Computing such designs is generally an NP-hard problem and one can instead rely on a convex relaxation that considers probability distributions over the samples. Although greedy strategies and rounding procedures have received a lot of attention, straightforward sampling from the optimal distribution has hardly been investigated. In this paper, we propose theoretical guarantees for randomized strategies on E and G-optimal design. To this end, we develop a new concentration inequality for the eigenvalues of random matrices using a refined version of the intrinsic dimension that enables us to quantify the performance of such randomized strategies. Finally, we evidence the validity of our analysis through experiments, with particular attention on the G-optimal design applied to the best arm identification problem for linear bandits.
Best Arm Identification in Graphical Bilinear Bandits
Dec 14, 2020
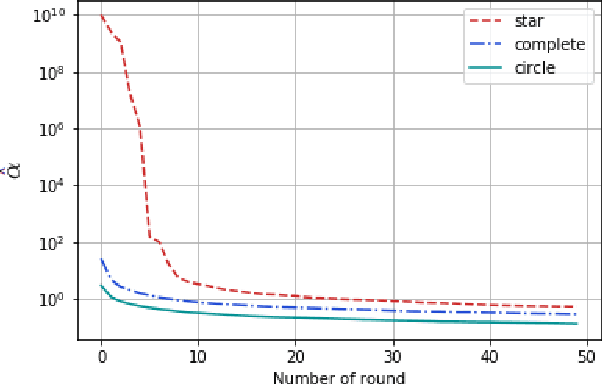

Abstract:We introduce a new graphical bilinear bandit problem where a learner (or a \emph{central entity}) allocates arms to the nodes of a graph and observes for each edge a noisy bilinear reward representing the interaction between the two end nodes. We study the best arm identification problem in which the learner wants to find the graph allocation maximizing the sum of the bilinear rewards. By efficiently exploiting the geometry of this bandit problem, we propose a somehow \emph{decentralized} allocation strategy based on random sampling with theoretical guarantees. In particular, we characterize the influence of the graph structure (e.g. star, complete or circle) on the convergence rate and propose empirical experiments that confirm this dependency.
Randomization matters. How to defend against strong adversarial attacks
Feb 26, 2020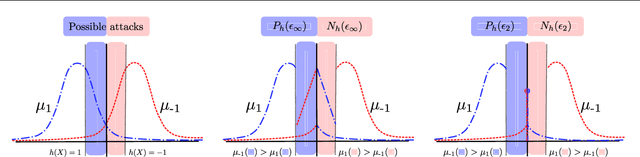

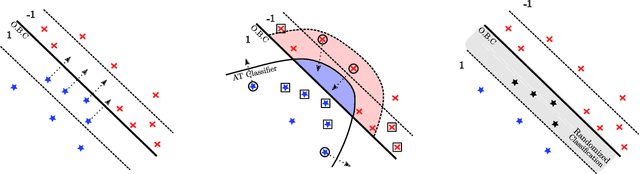
Abstract:Is there a classifier that ensures optimal robustness against all adversarial attacks? This paper answers this question by adopting a game-theoretic point of view. We show that adversarial attacks and defenses form an infinite zero-sum game where classical results (e.g. Sion theorem) do not apply. We demonstrate the non-existence of a Nash equilibrium in our game when the classifier and the Adversary are both deterministic, hence giving a negative answer to the above question in the deterministic regime. Nonetheless, the question remains open in the randomized regime. We tackle this problem by showing that, undermild conditions on the dataset distribution, any deterministic classifier can be outperformed by a randomized one. This gives arguments for using randomization, and leads us to a new algorithm for building randomized classifiers that are robust to strong adversarial attacks. Empirical results validate our theoretical analysis, and show that our defense method considerably outperforms Adversarial Training against state-of-the-art attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge